Метод замены переменной

Теорема 1.Если функциянепрерывна, а функциянепрерывно дифференцируема, то.

Это равенство можно также записать в виде .

Следствие (метод подведения под знак дифференциала) Пусть функции,,непрерывны, тогда.

Метод интегрирования по частям

Теорема 2.Пусть функцииинепрерывно дифференцируемы, тогда

.

Последнюю формулу часто записывают в сокращенном виде .

Этот метод применяется в случае, когда подынтегральная функция имеет вид произведения , где- многочлен, а- тригонометрическая, показательная, обратная тригонометрическая, или логарифмическая функция.

Интегрирование функций, содержащих квадратный трехчлен

Рассмотрим метод нахождения интегралов вида

и.

. Выносим из квадратного трехчленакоэффициентa и выделяем в нем полный квадрат следующим образом.

где.

Делаем в интеграле замену переменной,, в результате он приводится к виду или.

Записываем интеграл в виде суммы двух интегралов в соответствии с двумя слагаемыми числителя. В первом интеграле делаем замену переменной. В результате оба слагаемых - табличные интегралы.

Интегрирование рациональных функций

Рациональной функцией (рациональной дробью) называется отношение двух многочленов:

.

Рациональная функция , у которой степень числителя меньше степени знаменателя () называется правильной. Если же, то такая дробь называетсянеправильной.

Рассмотрим способы нахождения интегралов вида , гдеи- некоторые многочлены переменной. Простейшие из них:

.

Прик .

Метод интегрирования дроби был рассмотрен в этой лекции выше.

Теперь рассмотрим подход к интегрированию рациональных функции в общем случае. 1⁰)Если подынтегральная дробьнеправильная, то сначала путем деления числителя на знаменатель выделим целую часть (многочлен). 2⁰)Если знаменатель правильной дроби разлагается на множители видаи(- натуральные, дискриминант квадратного трехчлена отрицателен), то дробь разлагается на сумму простейших дробей следующим образом:

Таким образом, любую рациональную дробь можно записать в виде суммы многочлена и простейших дробей, каждую из которых можно проинтегрировать с помощью элементарных функций. Тем самым доказана следующая теорема.

Теорема.Первообразная от любой рациональной функции есть элементарная функция.

Интегрирование некоторых иррациональных функций

Рассмотрим теперь нахождение интегралов вида , где- рациональная функция, т.е. отношение двух многочленов, содержащих переменнуюx и степенные функции вида. Обозначим через- наименьший общий знаменатель дробейи сделаем в исходном интеграле замену переменной ,. В результате получим интеграл от рациональной функции переменной

.

Поскольку все числа - целые, как было отличено выше, такой интеграл всегда находится в элементарных функциях.

Интегралы вида ,

где - рациональная функция с помощью замены переменной

,

где также сводятся к интегралам от рациональных функций.

Интегрирование некоторых тригонометрических функций

Рассмотрим нахождение интегралов вида ,где- рациональная функция. Такие интегралы с помощью универсальной замены переменной всегда сводятся к интегралам от рациональных функций.

, где- рациональная функция. )Если подынтегральная функция является нечетной по косинусу, т.е. если, то она может быть преобразована к виду

,

после чего в интеграле делается замена переменной и он сводится к интегралу от рациональной функции:. ) Если подынтегральная функция является нечетной по синусу, т.е. , то она может быть преобразования к видуи . ) Если подынтегральная функция удовлетворяет условию , то она может быть преобразована к виду, после чего в интеграле делается замена,,, и он сводится к интегралу от рациональной функции.

Интегрирование функции вида , где- рациональная функция

С помощью выделения полного квадрата в квадратном трехчлене и замены переменной интегралприводится к одному из следующих трех видов (-рациональная функция). ) . Здесь с помощью замены переменной, этот интеграл преобразуется к виду. ) Интегралы виданаходятся с помощью замены,

.

)Интегралы виданаходятся с помощью замены,

. ) Интегралы вида находятся с помощью замены переменной,. ) Интеграл, где- многочленn-ой степени можно записать в виде

,

где - некоторый многочлен степени,-число. Коэффициентыинаходятся методом неопределенных коэффициентов после дифференцирования обеих частей записанного равенства.

В заключение отметим, что класс функций, первообразные которых находятся в виде элементарных функций (говорят интегрируемых в квадратурах) довольно узок. Например, невозможно записать с помощью элементарной функции.

Приложения неопределенного интеграла в экономике

Пусть чистые инвестиции I определяют прирост основного капитала фирмы К в единицу времени, то есть I( t ) = dK( t )/dt = K' ( t ). В этом случае, основной капитал К фирмы определяется как неопределенный интеграл от инвестиций I :K( t ) =   I( t ) dt = Kt + c = Kt  + K0, где К0 – начальный капитал фирмы.

Пример 1. Чистые инвестиции заданы в виде следующей функции I( t ) = 100 t^2/3 тыс. тенге в единицу времени и начальный капитал фирмы в момент t = 0 равен 200 тыс.тенге. Определить основной капитал фирмы К, как функцию зависящую от времени и исходного капитала.

Решение: По определению: К( t ) =  100 t^2/3 dt = 100  t^2/3 dt = 100 ( 3/5 t^5/3 ) + c. Отсюда, K( t ) = 60 t^5/3 + 200 ( тыс.тенге ).

Функция потребления С определяет планируемый или желаемый уровень потребительских расходов в зависимости от располагаемого дохода Y т.е. C = C(Y).Предельная склонность к потреблению MPC - это прирост потребления при увеличении личного дохода на единицу. Таким образом, MPC (Y) = dC/dY = C' (Y).Следовательно, функция потребления представляет собой неопределенный интеграл от предельной склонности к потреблению: C(Y) =  MPC dY.

Пример 2. Предельная склонность к потреблению равна 0,7 и необходимые потребительские расходы при нулевом доходе ( Y = 0 ) равны 30.Найти соответствующую функцию потребления C = f( Y ). Решение: C( Y ) =  MPC dY =  0,7 dY = 0,7 Y + c, т.к. при Y = 0 C(0)=30, получим, что C( Y ) = 0,7 Y + 30.

Функция сбережений S определяет планируемый или желаемый уровень сбережений в зависимости от располагаемого личного дохода Y, т.е. S = S( Y ).Предельная склонность к сбережениям MPS - это прирост сбережений при увеличении дохода на одну единицу. Таким образом, MPS(Y) = dS/dY = S' (Y).Следовательно, функция сбережений представляет собой неопределенный интеграл от предельной склонности к сбережениям: S(Y) =   MPS dY.

Пример 3. Наблюдаем прямую связь с предыдущим примером, т.к. что не потребляется, то сберегается, т.e. предельная склонность к сбережениям, очевидно, равна 0,3 и сбережения соответствующие уже сделанным потребительским расходам при нулевом доходе равны - 30, отрицательные значения сбережений представляют собой долги. Найти соответствующую функцию сбережений. Решение: S(Y) =  MPS dY =  0,3 dY = 0,3 Y + с, т.к. S( 0 ) = - 30, то с = - 30. Окончательно: S(Y) = 0,3 Y - 30.

Осн.лит.: 2, глава 5 § 5.1, [205-207] , 7, глава 6 §1, [183-189], 25.

Контрольные вопросы:

1. Дайте определенияпервообразной функции инеопределенного интеграла.

2. Перечислите основные методы интегрирования.

3. Как рациональную дробь разложить на элементарные дроби?

4.Перечислить все случаи интегрирования функции видаR(sinx,cosx).

Лекция 7. Определенный интеграл и его свойства. Формула Ньютона-Лейбница. Методы интегрирования определенного интеграла. Несобственный интеграл. Приложения определенного интеграла в экономике.

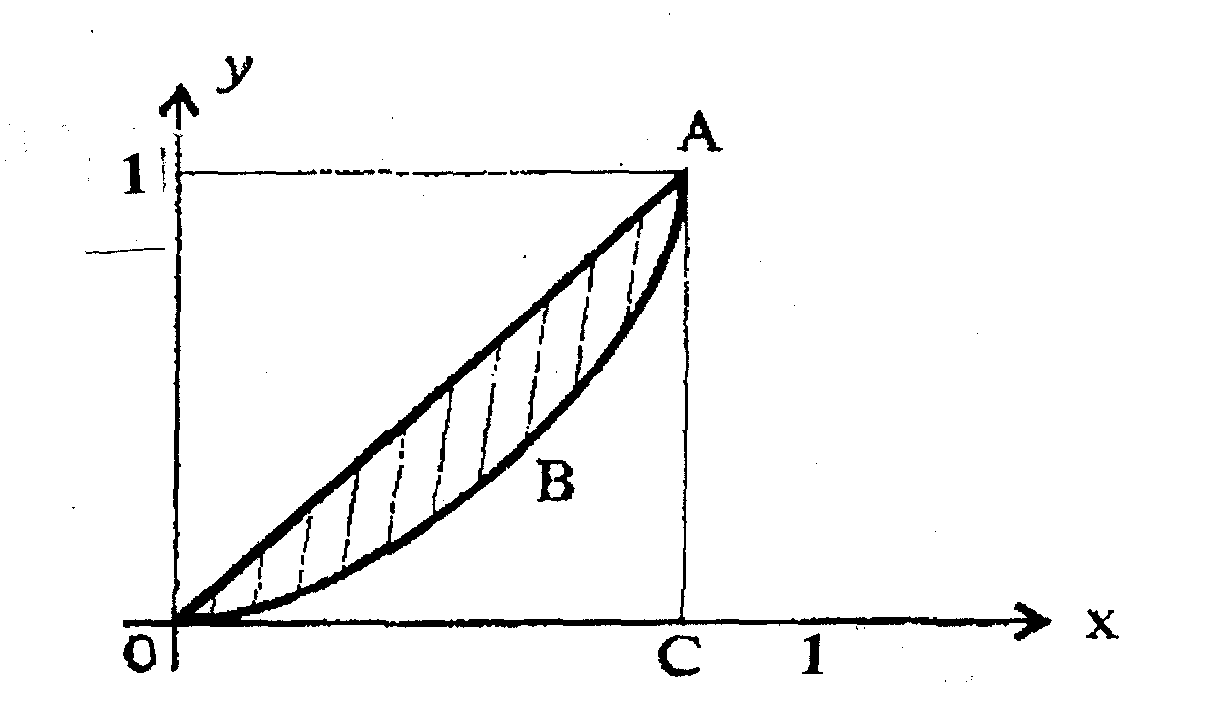
Определение: Криволинейной трапецией называется область на плоскостиограниченная осью, прямыми,гдеи графиком непрерывной на отрезкефункции(см. рис.1).

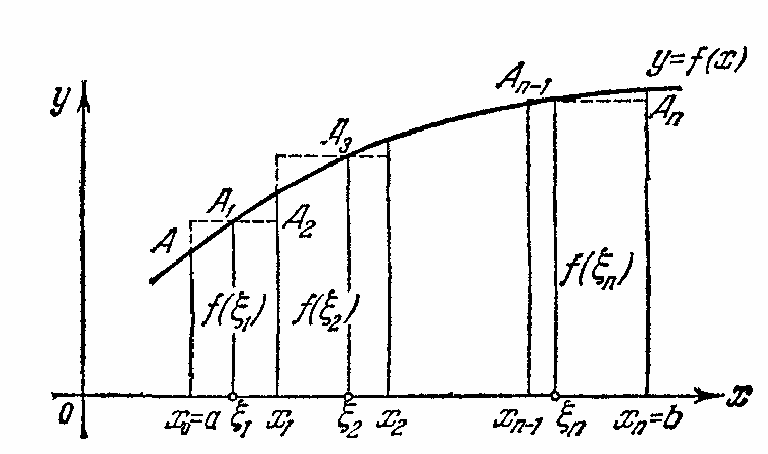
Р

Рис.1

азбиением отрезка наn частей называется набор чисел из этого отрезка, гдеи.

В каждом отрезке (элементарном участке) разбиения выберем некоторую точку. Такое разбиение будем обозначать буквой, а длину элементарного участка обозначим через. Пусть на отрезкеопределена некоторая функция.

Определение. Интегральной суммой для функции , построенной по разбиениюотрезка, называется сумма произведений значений функции в выбранных точкахна длины элементарных участков.

Обозначение: .Еслив , то приближенно равна площади соответствующей криволинейной трапеции.

Определение. Определенным интегралом от функции на отрезкеназывается предел интегральных сумм этой функции по разбиениям, у которых максимальныйстремится к нулю, т.е.. Еслив, то этот интеграл выражает точную площадь соответствующей криволинейной трапеции.

Теорема 1. Если функция непрерывна на отрезкеили имеет на нем конечное число точек разрыва первого рода, то эта функция интегрируема на, т.е.существует.

Свойства определенного интеграла

В дальнейшем будем считать, что все рассматриваемые функции – интегрируемы.

1) ,-постоянная. 2) Если на, то. 3) Оценка определенного интеграла снизу и сверху. Если на отрезке функцияограничена снизу и сверху числамиm и , т.е. если на, то. 4) Теорема о среднем. Пусть функциянепрерывна на отрезке, тогда на этом отрезке найдется такая точкаc, что . Это значение называется средним значением функции на. 5) Оценка модуля определенного интеграла. . 6) Свойство линейности.7) Свойство аддитивности. Если выполняется неравенство , то. Интегралсчитается равным нулю. Свойство аддитивности справедливо (при условии существования интегралов) для чиселрасположенных в любом порядке, т.е. требованиездесь не обязательно.

Производная интеграла по верхнему пределу и формула Ньютона – Лейбница

Пусть функцияинтегрируема в отрезкеи. Определим новую функциюдляс помощью соотношения.

Теорема 2. Если функция непрерывна в, то функцияявляется первообразной для функциив, т.е. в этом интервале.

Теорема 3. (Ньютона - Лейбница) Пусть функция непрерывна на отрезкеи функцияесть ее первообразная на этом отрезке, тогда

.

Замена переменной в определенном интеграле

Теорема 4. Пусть функция непрерывна в отрезке, а функциямонотонная и непрерывно дифференцируема в отрезке, где,, тогда.

Нахождение определенного интеграла по частям

Теорема 5. Пусть функции инепрерывно дифференцируемы в отрезке, тогда верно равенство. Сокращенная запись:.

Несобственные интегралы с бесконечными пределами

1) Пусть функция непрерывна в промежутке .Несобственным интегралом от a до от этой функции называется предел:.

Если этот предел существует (равен числу), то несобственный интеграл здесь и в дальнейшем называется сходящимся; если он не существует, то интеграл называется расходящимся. В случае, если в промежутке, такой интеграл выражает площадь неограниченной фигуры с границами:,и графиком функции. Для сходящегося интеграла эта площадь конечна, для расходящегося – бесконечна.

Формула Ньютона-Лейбница для таких несобственных интегралов имеет вид:

.

2) Пусть теперь функция непрерывна в промежутке. Тогда несобственным интегралом отдоназывается предел

. По формуле .

3) Если функция непрерывна на всей числовой оси, то несобственным интегралом от до называется следующая сумма двух интегралов(здесь- некоторое число).

Это определение не зависит от выбора . Такой интеграл называетсясходящимся, если сходятся оба интеграла: и.

Если хотя бы один из этих интегралов расходится, то интеграл называетсярасходящимся. Вычислим: .

Приложения определенного интеграла в экономике

Пример 1. Пусть функцияописывает изменение производительности некоторого производства с течением времени. Найдем объем продукцииu, произведенный за промежуток времени.

Если производительность за промежуток времени не изменяется с течением времени, то объем продукциипроизведенный за этот промежуток задается формулой. Разобьем отрезокна промежутки времени точкамиВ общем случае объем продукции, выпущенной за промежуток времени, равенгдеСледовательно,,. Окончательно получим, что объем выпускаемой продукции за промежуток времениравен. Величина этого объема численно равна площади криволинейной трапеции, ограниченной графиком функции производительности трудана промежутке.

2. Исследуякривую Лоренца– зависимость доли совокупного дохода обществаот долиимеющего ее населения (кривую, рис. 1), можно оценить степень неравенства в распределении доходов населения. При равномерном распределении доходов кривая Лоренца преобразуется в прямую - биссектрису, поэтому площадь фигурымежду биссектрисойи кривой Лоренца, отнесенная к площади треугольника(коэффициент Джини ),характеризует степень неравенства в распределении доходов населения.

, так как.

3. Излишек потребителя(добавочная выгода покупателя). Пусть(Q) – кривая спроса некоторого товара,- равновесная цена, Q₀- реализуемое по этой цене количество товара (см. рис.2). Излишек потребителя (consumersurplus)– это разность между гипотетическими затратами потребителей, которые могли бы быть, и реальными затратами в условиях рынка, равными Q_0, определяется по формуле: .

Рис.1

Излишек потребителя CS Точка равновесия (Q) Q0 Q Рис. 2

4. Излишек производителя(добавочная выгода продавца). Пусть- кривая предложения некоторого товара,- равновесная цена (см. рис.3).

P

P₀ Излишек производителя PS

Точка равновесия

Q₀ Q

Рис. 3

Излишек производителя, обозначаемый PS (producersurplus), вычисляется по формуле.

5. Пусть требуется вычислить капитал фирмы К, образуемого в начальный момент становления фирмы только за счет инвестиций I. Прирост капитала фирмы в единицу времени равен 3t^1/2 тыс.тенге в месяц .Определить величину капитала, образованного за первые четыре месяца.

Решение: Капитал фирмы можно рассмотреть как сумму капиталов, образованных на бесконечно малых частичных отрезках длиной  t_i, на которые поделен отрезок [ 0,4 ] : 0 = t₀ < t₁ < t₂ <...< tn = 4.Будем считать, что на каждом таком малом частичном интервале функция I( t ) не меняется и капитал, образованный на каждом частичном интервале равен произведению I( t )  t_i . Сумма капиталов, образованных на всех бесконечно малых частичных отрезках представляет собой интегральную сумму. lim  I(t_i)t_i===( 2t^3/2 )= 16 тыс.тенге.

Осн. лит.: 2, Глава 7, § 7.1, [275-292], 12, Глава 11 §1-7,[278-302], § 8,9 [294-302], [310-312] 25, глава 6 § 6-10,[374-395]

Контрольные вопросы:

1. Дайте определение определенного интеграла

2. Сформулируйте основные свойства определенного интеграла

3. Приведите формулу Ньютона-Лейбница.

4. Приведите основные методы интегрирования определенного интеграла.

Лекция 8.Основные понятия о функциях нескольких переменных. Дифференцирование. Экстремумы. Функция нескольких переменных в экономических задачах.

Основные понятия о функциях нескольких переменных

Определение. Пусть имеетсяпеременных величин и каждому набору их значенийиз некоторого подмножествасоответствует вполне определенное значение переменной величины. Тогда говорят, что задана функция нескольких переменных. Переменныеназываются независимыми переменными или аргументами,- зависимой переменной, а символозначает закон соответствия. Множествоназывается областью определения функции.

Рассмотрим случай функции двух (трех) переменных, позволяющий использовать наглядную геометрическую иллюстрацию основных понятий настоящей главы.

Пусть - некоторое подмножество на плоскости(в пространстве).

Определение. Если каждой точке областисоответствует одно вполне определенное число - значение переменной величины, то говорят, что задана функция двух (трех) переменных:.

При этом символ обозначает закон соответствия,- область определения функции, а множество- область ее значений (см. рис. 1).

Рис. 1

Рис. 2

Рис. 3

Например, в экономических исследованиях область определения можно рассматривать как подмножество пространства благ, где- количество-го блага.. К базовым понятиям экономической теории относятся: 1)функция полезности, выражающая полезностьот двух приобретенных товаров в количествеисоответственно. 2)производственная функция, выражающая результат производственной деятельностиот обусловивших его значений факторови.Наиболее часто встречающийся вид такой функции– производственная функция Кобба-Дугласа: , где- положительные константы. Здесь- величина общественного продукта,- затраты труда,- объем производственных фондов.

Окрестностьюточкина плоскости (илив пространстве) радиусаназывается круг без окружности (или шар без сферы) радиусас центром в точке. Такую окрестность будем обозначать через.

Здесь n=2 или 3. Если, то(см. рис. 2).

Линии и поверхности уровня. Пусть– число.Линией уровняфункции называется множество всех точекиз области определения, координаты которых удовлетворяют уравнению. Например, линии уровня функции, изображенные на рис.3, соответствуют значениям.

Поверхностью уровня функцииназывается множество всех точекиз области определенияфункции, координаты которых удовлетворяют уравнению

Предел и непрерывность функции нескольких переменных

Определение.Числоназываетсяпределом функциив точке, если для каждогонайдется такое числочто при всехиз окрестности, кроме этой точки, выполняется неравенство. Соответствующее обозначение:

.

Определение.Функцияназываетсянепрерывнойв точкеесли выполняется три условия: 1) существует, 2) существует значение функции в точке, 3) эти два числа равны между собой, т.е..

Частные приращения и частные производные

Определение.Частным приращениемпоxфункциив точкесоответствующим приращениюназывается разность.

Аналогично, частным приращением по в точкефункциисоответствующим приращениюназывается разность.

Определение.Частной производной поxфункциив точкеназывается предел отношения частного приращения поxэтой функции в указанной точке к приращениюаргументаx, т.е.. Частные производные обозначаются символами,,,. Аналогично,частная производная пов точке: и ,,. Частные производные функций находятся по известным правилам дифференцирования функции одной переменной, при этом все переменные, кроме той, по которой дифференцируется функция, считаются постоянными. Так при нахождении для функции переменнаяпринимается за постоянную, а при нахождении- постояннаяx.

Пусть - производственная функция. Тогда, ее частная производная, например, окажется приближенно равна той дополнительной продукции, которая может быть получена при увеличении количества факторана единицу. Это дополнительное количество продукции называютпредельной производительностьюилипредельным продуктом фактора.

Введем понятие применяемой в экономической теории частной эластичностифункции нескольких переменных относительно переменной

.Значениепоказывает приближенно, на сколько процентов изменится переменнаяпри изменении переменнойна 1%. Например, для производственной функции Кобба-Дугласа, т.е. показателииприближенно показывают на сколько процентов изменится выпуск продукциипри изменении затрат трудаили только объема производственных фондовна 1%.

Если функция имеет частные производные, то еечастными дифференциаламиназываются выражения и. Здесь и .

Частные дифференциалы являются дифференциалами функций одной переменной полученными из функции двух переменных при фиксированныхилих.

Полным приращением функции в точке, соответствующим приращениямиаргументов, называется разность .

Определение.Если полное приращение функциив точкеможно представить в виде

, (1)

где и– постоянные, аибесконечно малые при, то выражениеназываетсяполным дифференциаломэтой функции в точке.

Полный дифференциал называют также главной частью приращения функции.Функция, имеющая полный дифференциал в некоторой точке, называетсядифференцируемой в этой точке.

Теорема 1. Пусть функцияи ее частные производныеинепрерывны в некоторой окрестности точки. Тогда функциядифференцируема в точкеи ее полный дифференциал равен сумме частных дифференциалов:.

Если в формуле (1) отбросить бесконечно малые ии заменить полное приращение приближенно полным дифференциалом, то получим следующуюформулу для приближенного нахождения значений функциис помощью полного дифференциала.

++.

Полный дифференциал функции большего числа переменных находится по формуле++ … +.

Пусть имеется функция двух переменных и функция одной переменной, тогда производная похсложной функцииназываетсяполной производнойи обозначается через.Функция, заданная с помощью уравненияназывается неявной.

Теорема 3.Пусть функцияи ее частные производныеинепрерывны в окрестности точки, гдеи. Тогда уравнениезадает в некоторой окрестности точкидифференцируемую функциюи в этой окрестности ее производная равна.

Функция , заданная с помощью уравненияназывается неявной функцией двух переменных.

Теорема 4.Пусть функцияи ее частные производные,,непрерывны в окрестности точки, гдеи, тогда уравнениезадает в некоторой окрестности точкидифференцируемую функциюи в этой окрестности ее частные производные равны

,.

Частной производной –го порядка функцииназывается частная производная от одной из ее производныхпорядка. Сама функциясчитается производной нулевого порядка. Перечислим четыре производных второго порядка:

, , ,.

Производных –го порядка у функции двух переменных имеется.

Частная производная функции, в которой присутствуют дифференцирования по разным переменным, называется смешаннойпроизводной. Смешанными производными второго порядка у функции двух переменных являютсяи.

Теорема о смешанных производных. Пусть функцияи ее производные,,,непрерывны в некоторой окрестности точки. Тогда в этой точке ее смешанные производные второго порядка равны между собой:.

Следствие.Пусть все частные производные функциидо–го порядка включительно и все ее смешанные производные–го порядка непрерывны в некоторой окрестности точки. Тогда в этой точке ее смешанные производные–го порядка, отличающиеся только очередностью дифференцирования, совпадают.

Производная по направлению.

Найдем скорость изменения функции трех переменных при перемещении из точки в направлении единичного вектора, определяемого своими координатами – направляющими косинусами:. Для этого рассмотрим прямую, проходящую через точкус направляющим вектором. Ее параметрические уравнения имеют вид

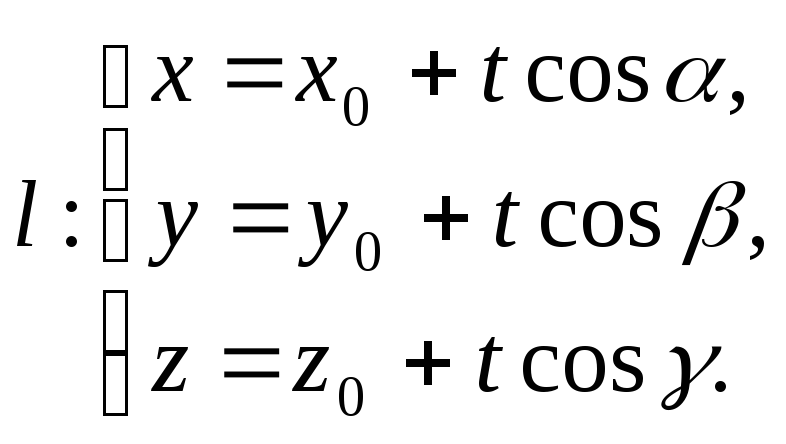
Пусть точка .

Определение. Производной функции по направлению векторав точкеназывается предел: . Этот предел обозначается. Обозначая, получим, что . Но

.

Полагая , получим формулу для определения производной функциипо направлениюв точке:.

Градиент функции нескольких переменных.

Определение. Вектор с координатами – частными производными функцииназываетсяградиентомэтой функции и обозначается:

Для произвольного ненулевого вектора ,.

Рис.4

Рис. 5

Рис. 6

Свойства градиента

1)совпадает с проекцией векторана вектор:.2)максимальна в направлении, совпадающим с:, т.е. градиент указывает направление наибольшего возрастания функции и его модуль равен производной по этому направлению. В экономических задачахуказывает направление наибольшего роста прибыли, если- прибыль, а антиградиент (-) направление наибольшего убывания издержек, если- издержки. 3) В экстремальных точках функцииее частные производные равны нулю (если они существуют). Точки, в которых все координаты градиента равны нулю, называютсясингулярными(или критическими) точками функции. Точки, в которых градиент отличен от нуля, называютсярегулярными.

Теорема.Через любую регулярную точкуфункцииможно провести касательную плоскость к ее поверхности уровня, проходящей через, и эта плоскость перпендикулярна.

Уравнение касательной плоскости:

.

Градиент функции двух переменных (или) перпендикулярен касательной к линии уровня этой функции, проходящей через точкуM₀ (см. рис. 5),и уравнение этой касательной можно записать в виде:

.

Прямая, перпендикулярная касательной плоскости к поверхности в точке касанияназываетсянормалью к этой поверхности. Ее параметрические уравнения имеют вид

Экстремумы функции нескольких переменных

Точка называетсяточкой максимумафункции, если существует окрестностьтакая, что для всехиз этой окрестности выполняется неравенство.Если для всехиз окрестностивыполняется неравенство,то точканазываетсяточкой минимума. Значение функции в точке максимума, называетсямаксимумом функции, а ее значение в точке минимума –минимумом. Точки максимума и минимума называютсяэкстремальными точкамифункции, а максимумы и минимумы называютсяэкстремумамифункции (рис. 6).

Пусть функция определена в некоторой окрестности точки. Если вкаждая частная производнаяиравна нулю или не существует, тоназываетсякритической точкойфункции.

Теорема 1.(Необходимое условие экстремума). Еслиявляется экстремальной точкой функции, то– критическая точка этой функции.

Сформулируем необходимые условия экстремума для дифференцируемой функции nпеременных: Если точкаявляется экстремальной точкой функции, дифференцируемой в некоторой окрестности, то-стационарная точкаэтой функции, то есть ее координаты удовлетворяют системе

Теорема 2. (Достаточные условия экстремума). Пусть функциятрижды дифференцируема в некоторой окрестности своей критической точки. Обозначим,,,. Тогда: 1) Если, то точкаэкстремальная для функции, причем если, то это точка минимума, а если, то точка- точка максимума. 2) Если, то в точкеэкстремума нет.

Пусть - стационарная точка трижды дифференцируемой в окрестностифункции. Обозначими составимnопределителейk-го порядка:, гдеk=1,2,…,n.

Теорема (критерий Сильвестра). Если все дляk=1,2,…,n, то - точка минимума функции .Если же дляk=1,2,…,n, то - точка максимума этой функции.

Условные экстремумы

Пусть в области определения функции имеется линия, определяемая уравнением. Точканазываетсяточкой условногомаксимумафункции, если у этой точки существует такая окрестность, что для всех точекиз пересечения этой окрестности свыполняется неравенство. В этой же ситуацииточка условного минимумаопределяется неравенством. Точки условных максимумов и минимумов называютсяточками условных экстремумов, а значения функциив этих точках называютсяусловными экстремумами (условными максимумами или минимумами).

Если кривая задается с помощью графика явной функции, то задача нахождения условных экстремумов функциисводится в задаче нахождения экстремумов функции одной переменной.

Метод Лагранжа для нахождения условных экстремумов

Пусть линия , определяемая уравнением, находится в области определения функции.Функцией Лагранжаназывается функция трех переменных

. Здесь–произвольный параметр.

Теорема Лагранжа.Пусть функции идифференцируемы в окрестности точки. Если точкаявляется точкой экстремума функциипри условии, то точкадля некоторогоявляется стационарной точкой функции Лагранжа, то есть числаявляются решением системы

Эта теорема переносится и на случай функции nпеременныху которой переменные связаныmуравнениями связи

. Здесь все функции непрерывно дифференцируемы. Функция Лагранжа для такой задачи имеет вид

ПримерРассмотрим задачу выбора двух товаров в количестве x₁и x₂, максимизирующих функцию полезности U(x₁, x₂) и удовлетворяющих бюджетному ограничениюp₁ x₁+ p₂ x₂ =I, где р₁, р₂ -цена 1-ой единицы i-го товара, =i, 2, I - бюджет потребителя.

Решение: Функция Лагранжа имеет вид: F (x₁, x₂, y) = U(x₁, x₂) + y(I- p₁ x₁ – p₂x₂). Необходимые условия экстремума функции Лагранжа:

,

Графическое решение этой задачи изображено на рисунке 7.

Рис. 7

Решением является точка касания бюджетной прямой с кривой безразличия функции. В точкеприобретение товаров укладывается в бюджет, но значение функции полезности меньше,. В точкене израсходован весь бюджет, следовательно, на оставшиеся средства можно приобрести товары и тем самым улучшить их полезность. В точкезначение функции полезности больше, но расход на товары превысил имеющийся бюджет.

Функции нескольких переменных в экономических задачах.

В социально-экономических исследованиях возникает необходимость установить функциональную зависимость между данными, полученными в результате наблюдений. Широко распространенным методом решения таких задач является метод наименьших квадратов. Он основан на том, что из множества функций вида, приближающих имеющиеся значения, искомой считается та, для которой сумма квадратов отклонений наблюдаемых значений от вычисленных является наименьшей. Определить вид этой функции, называемойэмпирической формулой, можно исходя из характера расположения на координатной плоскости опытных (эмпирических) данных.

Метод наименьших квадратов.

Пусть в результате наблюдений получены следующие данные:

			…		…
			…		…

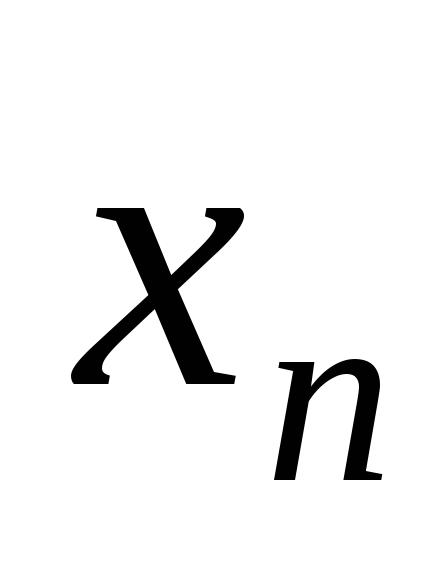
Предполагая, что между исуществует зависимость вида, найдем значения параметровитак, чтобы величинапринимала наименьшее значение (см. рис. 7).

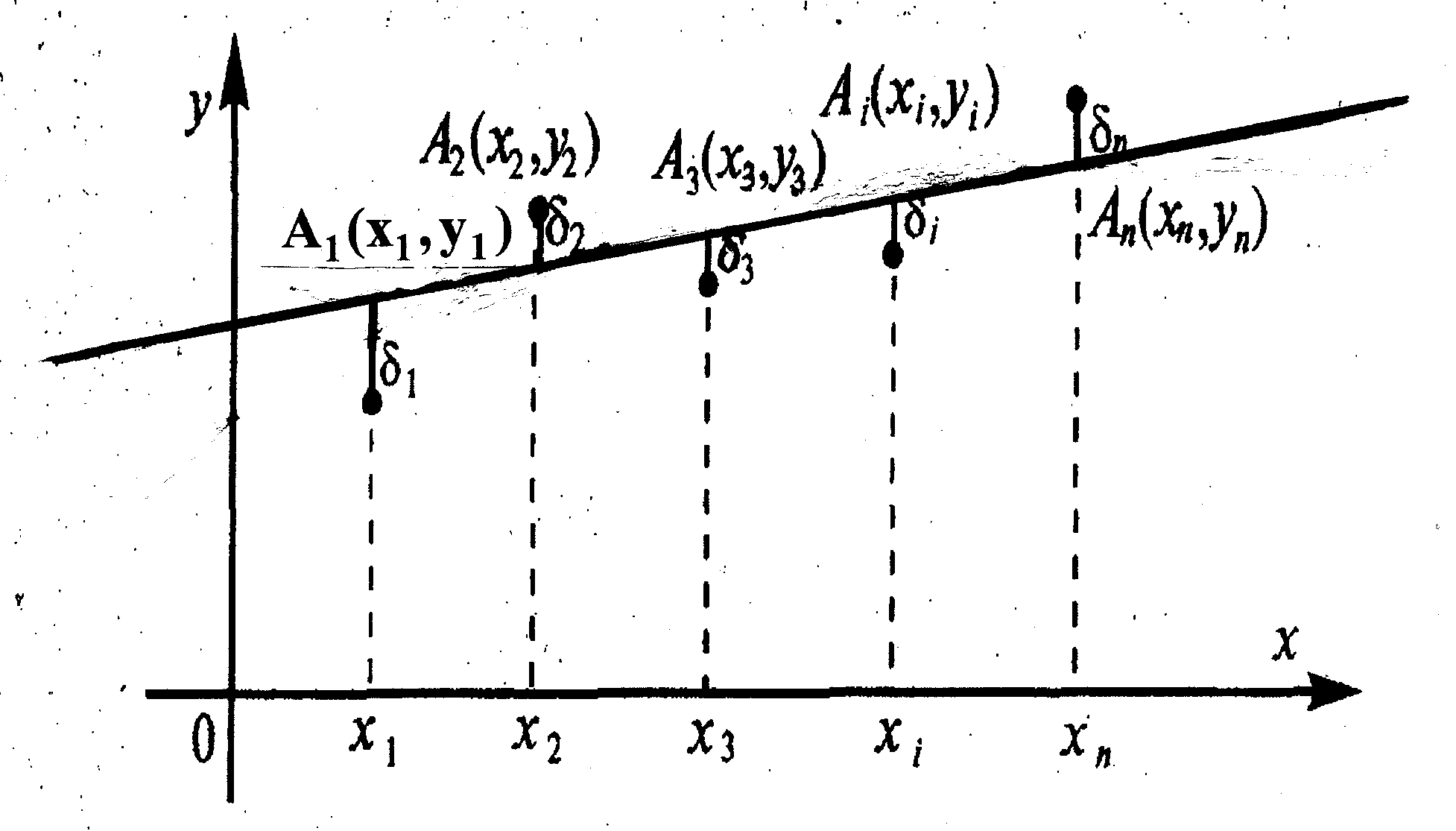Рис. 8

Для этого необходимо, чтобы частные производные функции по каждой переменной обращались в нуль, т.е.и.

Получим систему двух уравнений, которую называют нормальной системой уравнений.

Решив эту систему и подставив найденные значенияив уравнение, получим искомую эмпирическую формулу. Если- квадратичная функция, т.е., то, а неизвестные параметрыопределяются из системы нормальных уравнений:

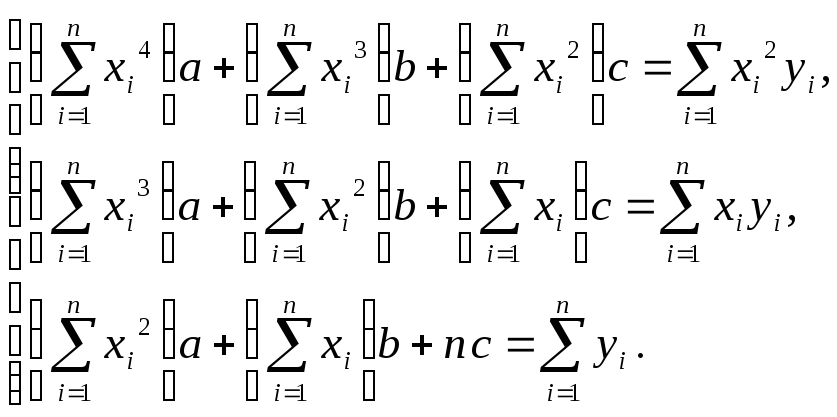
Если , то, а неизвестные параметрыиопределяются из системы нормальных уравнений:

В экономических задачах теории потребления существенную роль играет следующая важнейшая характеристика исследуемого процесса перекрестная эластичность спроса. Понятие взаимосвязанности относится к товарам, для которых изменение цены одного товара влечет за собой изменение спроса на другой товар. Такие товары делятся на два типа: взаимозамещаемые и взаимодополняющие. Взаимозамещаемые - это товары, для которых увеличение ( уменьшение) цены одного товара при неизменной цене другого влечет за собой увеличение (уменьшение) спроса на этот другой товар. Примером взаимозамещаемых товаров являются масло и маргарин. Взаимодополняющие - это товары, для которых увеличение (уменьшение) цены одного при неизменной цене другого влечет за собой уменьшение (увеличение) спроса на этот другой товар. Примером взаимодополняющих товаров являются автомобиль и бензин. В пространстве товаров при постоянном уровне потребления взаимозамещение товаров характеризуют с помощью так называемой перекрестной эластичности, показывающая изменение спроса на один товар при изменении цены взаимосвязанного с ним другого товара. Перекрестная эластичность спроса показывает на сколько процентов изменится спрос на i-ый товар, если цена j-го товара изменится на один процент. В зависимости от знака данного коэффицента товары делятся на взаимозаменяемые  и вэаимодополняемые  . Перекрестная эластичность спроса на i-ый товар при однопроцентном изменении цены на j-й товар определяется по следующей формуле:

Пример. На рынках города Алматы в условиях совершенной конкуренции функция рыночного спроса на яблоки, зависящая от рыночных цен на яблоки P_я , груши P_г и личного дохода потребителя Y имеет вид: Q_я = -1.5 P_я + 0.3 P_г + 0.001Y +180

Определить при Р_я = 200 тенге, Р_г = 400 тенге, Y = 50000 тенге перекрестную эластичность функции спроса Q по рыночной цене Р_г.

Решение:

E_г(Q) = 0.3 * 40/5 = 2.4 >0, следовательно, яблоки и груши являются взаимозаменяемыми товарами и спрос на яблоки изменится на 2.4 процента, если цена на груши изменится на один процент. Т.е если цену на груши увеличить на 4 тенге, то спрос на яблоки увеличится на 1.2 кг., а если цену на груши уменьшить на 10 тенге, то спрос на яблоки уменьшится на 3 кг.

50