Шатманов Ж

$$$ 1

Укажите события из следующих случаев:

1. Бросание монет

2. Форма монет

3. Выпадение герба

4. Выпадение надписи

5. Сила выбрасывания

6. Угол выбрасывания

$$$ 2

Некоторое изделие, выбранное из партии готовых изделий оказалось бракованным. Укажите испытание из следующих случаев:

1. Изделие оказалось бракованным

2. Изделие оказалось стандартным

3. Жесткая транспортировка

4. Неопытность мастера

5. Акт выборки

$$$ 3

В сосуде содержится вода при нормальном атмосферном давлении при температуре +20⁰. Событие- вода находится в жидком состоянии. Укажите вид события.

$$$ 4

В сосуде содержится вода при нормальном атмосферном давлении при температуре +20⁰. Событие-вода находится в твердом состоянии. Укажите вид события

$$$ 5

Из следующих событий укажите случайные события:

1. Вода находится в жидком состоянии при температуре +20⁰ при нормальное атмосферном давлении.

2. Вода находится в твердом состоянии при температуре +20⁰ при нормальном атмосферном давлении.

3. Родился ребенок мужского пола

4. Стрелок попал в цель.

5. Стрелок не попал в цель

$$$ 6

Из следующих событий укажите единственно возможные события:

1. Произведен выстрел из орудия. События: попадание и промах.

2. Произведен выстрел из орудия. События: попадание и осечке

3. Брошена монета. События: Герб и ребро

4. Брошена монета. События: Надпись и ребро.

5. При выстреле произошла осечка. События: попадание и промах.

$$$ 7

Из следующих событий укажите равновозможных события:

1. Брошена монета. События: Герб и надпись

2. Брошена монета. События: Герб и ребро

3. Брошена монета. События: Надпись и ребро

4. Произведен выстрел из орудия. События: попадание и осечка.

5. Произведен выстрел из орудия. События: попадание и промах.

$$$ 8

Вероятность случайного события удовлетворяет неравенству

$$$ 9

Для противоположных событий справедливы равенства

1.

2.

3.

4.

5.

$$$ 10

В урне находятся 8 шаров. Из них 3 белых и 5 черных шаров. Укажите благоприятствующее число появления белого шара.

$$$ 11

10 человек играют в городки. Сколькими способами они могут набрать команду из 4 человек на соревнования?

$$$ 12

Набирая номер телефона, абонент забыл две последние цифры. Сколько номеров ему придется набрать, чтобы дозвониться, если он помнит, что эти две цифры различны.

$$$ 13

Сколькими способами 5 книг разных авторов можно расставить на полке в один ряд?

$$$ 14

Укажите формулу вероятности суммы случайных событий и

$$$ 15

Укажите формулу вероятности суммы случайных событий и

$$$ 16

Укажите формулу вероятности суммы несовместных событий и

$$$ 17

Укажите формулу вероятности совместного появления двух зависимых событий и

$$$ 18

Укажите формулу вероятности совместного появления трех зависимых событий и

$$$ 19

Укажите формулу вероятности совместного появления двух независимых событий и

$$$ 20

Укажите формулу вероятности появления хотя бы одного из двух зависимых событий и

$$$ 21

Укажите формулу вероятности появления хотя бы одного из двух независимых событий и

$$$ 22

Вероятности появления каждого из трех независимых событий и равны . Вероятности противоположных событий- . Укажите формулу вероятности появления всех трех событий и

$$$ 23

Вероятности появления каждого из трех независимых событий и равны . Вероятность противоположных событий- . Укажите формулу вероятности появления только одного из событий.

$$$ 24

Вероятности появления каждого из трех независимых событий и равны . Вероятность противоположных событий- . Укажите формулу вероятности появления только двух событий.

$$$ 25

Вероятности появления каждого из трех независимых событий и равны . Вероятность противоположных событий- . Укажите формулу вероятности появления хотя бы одного события.

$$$ 26

Вероятности появления каждого из трех независимых событий и равны . Вероятность противоположных событий- . Укажите формулу вероятности не появления ни одного из этих события.

$$$ 27

Какова вероятность того, что последняя цифра наугад набранного телефонного номера окажется равной 5 или кратной 3?

$$$ 28

Жюри конкурса определило 10 претендентов, одинаково достойных первой премии. Среди них оказалось 5 научных сотрудников, 2 студента, 3 рабочих. Какова вероятность того, что в результате жеребьевки премия будет выдана или ученому или рабочему?

$$$ 29

Вероятность для компании, занимающейся строительством терминалов для аэропортов, получить контракт в стране равна 0,4, вероятность выиграть его в стране равна 0,3. Вероятность того, что контракты будут заключены и в стране и в стране , равна 0,12. Чему равна вероятность того, что компания получит контракт хотя бы в одной стране?

$$$ 30

В урне находятся 5 белых, 2 черных и 3 красных шара. Найти вероятность того, что из трех вытащенных по порядку шаров первый будет белым, второй - черным, третий - красным.

$$$ 31

Три орудия стреляют в цель. Вероятность попасть в цель из первого орудия равна 0,7 из второго -0,8, а из третьего -0,9. Найти вероятность того, что в цель попадет один снаряд.

$$$ 32

Три орудия стреляют в цель. Вероятность попасть в цель из первого орудия равна 0,7 из второго -0,8, а из третьего -0,9. Найти вероятность того, что в цель попадут два снаряда.

$$$ 33

Три орудия стреляют в цель. Вероятность попасть в цель из первого орудия равна 0,7 из второго -0,8, а из третьего -0,9. Найти вероятность того, что в цель попадут три снаряда.

$$$ 34

Три орудия стреляют в цель. Вероятность попасть в цель из первого орудия равна 0,7 из второго -0,8, а из третьего -0,9. Найти вероятность того, что в цель не попадет ни один снаряд.

$$$ 35

Три орудия стреляют в цель. Вероятность попасть в цель из первого орудия равна 0,7 из второго -0,8, а из третьего -0,9. Найти вероятность того, что в цель попадет хотя бы один снаряд.

$$$ 36

Три орудия стреляют в цель. Вероятность попасть в цель из первого орудия равна 0,7 из второго -0,8, а из третьего -0,9. Найти вероятность того, что в цель попадут хотя бы два снаряда.

$$$ 37

В первом ящике 2 белых и 10 черных шаров, во вторых ящике 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Вероятность, что оба шара белые?

$$$ 38

В первом ящике 2 белых и 10 черных шаров, во втором ящике 8 белых и 4 черных пара. Из каждого ящика по шару. Какова вероятность, один из вынутых шаров белый, а другой черный?

$$$ 39

В урне 2 белых и 7 черных шаров. Из нее последовательно внимают два шара. Какова вероятность того, этой 2-й шар окажется белым при условии, что 1-й шар был черным.

$$$ 40

Бросаются две игральные кости. Какова вероятность появления хотя бы одной шестерки?

$$$ 41

Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 5, а произведение равна 4.

$$$ 42

Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях четная, причем на грани хотя бы из костей появилась 6.

$$$ 43

Из колоды в 36 карт наугад одна за другой извлекаются две карты. Найти вероятность того, что ими оказались два короля.

$$$ 44

Задумано двухзначное число. Найти вероятность того, что задуманным числом окажется случайное названное двухзначное число?

$$$ 45

Задумано двухзначное число. Найти вероятность того, что задуманным числом окажется случайное названное двухзначное число, цифры которого различны

$$$ 46

Из колоды в 36 карт наудачу вынимают 2 карты. Найти вероятность того, что среди них окажется один туз?

$$$ 47

Из участков танцевального кружка, состоящего из 8 девушек и 4 юношей, выбирают 9 человек для танца. Найти вероятность того, что среди участников окажутся все юноши?

$$$ 48

Вероятность дожить человеку до 20 лет равны , дожить до 60 лет - . Какова вероятность дожить до 60 лет человеку 20-летнего возроста?

$$$ 49

Президент компании всегда приглашает одного из трех вице президентов присутствовать на бизнес - встречах и утверждает, что ее выбор кого-либо из троих - случаен. Однако один из вице президентов не был уже на трех последних встречах. Чему равна вероятность этого события, если выбор президента действительно случаен?

$$$ 50

Производится стрельба по мишени , состоящей из двух пересекающихся областей и . При этом вероятность попадания в область равна 0,5, а в область - равна 0,3. Найти вероятность попадания в область ?

$$$ 51

Производится стрельба по мишени , состоящей из двух непересекающихся областей и . При этом вероятность попадания в область равна 0,5, а в область - равна 0,3. Найти вероятность попадания в область ?

$$$ 52

В читальном зале имеется 6 учебников, из которых 3 в переплете. Библиотекарь наудачу взял 2 учебника. Найти вероятность того, что оба учебника окажутся в переплете?

$$$ 53

Вероятность того, что событие появится хотя бы один раз в 3-х независимых в совокупности испытаниях, равна 0,936. Найти вероятность появление события в одном испытании, считая, что во всех испытаниях вероятность появления события ода и та же?

$$$ 54

Вероятность того, что событие появится хотя бы один раз в 2-х независимых испытаниях равна 0,96. Найти вероятность появление события в одном испытании, считая, что во всех испытаниях вероятность появления события одна и та же?

$$$ 55

Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875. Найти вероятность попадания при одном выстреле, считая, что вероятность попадания при каждом выстреле одна и та же?

$$$ 56

Внутри эллипса 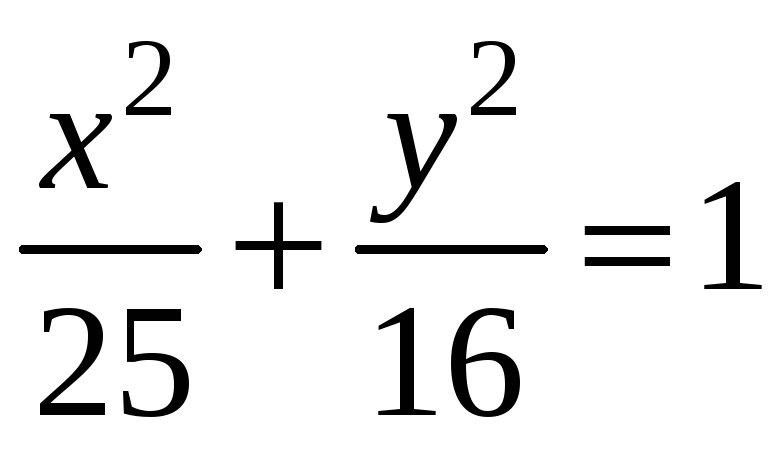расположен круг . Найти вероятность попадания точки в кольца, ограниченное эллипсом и кругом?

$$$ 57

Студент знает 20 из 30 вопросов программы. Найти вероятность того, что студент знает предложенные ему 2 вопроса?

$$$ 58

Студент пришел сдавать зачет, зная из 30 вопросов только 20. Какова вероятность сдать зачет, если после отказа отвечать на первый вопрос, преподаватель задает еще один?

$$$ 59

События образуют полную группу событий. Укажите формулу полной вероятности для события

$$$ 60

События образуют полную группу событий. Укажите формулу Байеса для события , которое уже произошло

$$$ 61

Вероятность того, что нужная сборщику деталь находится в первом ящике равна 0,6; во втором ящике – 0,7, в третьем ящике – 0,8. Найти вероятность того, что деталь содержится хотя бы в одном ящике?

$$$ 62

В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго, третьего элементов соответственно равны 0,1; 0,15; 0,2. Найти вероятность того, что тока в цепи не будет.

$$$ 63

Для схемы Бернулли с параметрами укажите формулу Бернулли

$$$ 64

Для схемы Бернулли укажите формулу локальной теоремы Муавра-Лапласа

$$$ 65

Для схемы Бернулли укажите формулу интегральной теоремы Муавра-Лапласа

$$$ 66

Для схемы Бернулли укажите формулу Пуассона

$$$ 66

Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти вероятность того, что событие наступит 20 раз в 100 испытаниях. Указание

$$$ 67

Вероятность появления события в каждом из независимых испытаний равна 0,8. Найти вероятность того, что событие наступит 120 раз в 144 испытаниях. Указание

$$$ 68

Найти вероятность того, что событие наступит 1400 раз в 2400 испытаниях, если вероятность появления этого события в каждом из независимых испытаниях равна 0,6. Указание

$$$ 69

Вероятность своевременного прибытия поезда на станцию равна 0,95. Найти вероятность того, что из 5-ти последовательно прибывших поездов 4 прибудут без опоздания

$$$ 70

Вероятность хотя бы одного попадания при двух выстрелах равна 0,96. Найти вероятность 3-х попаданий при 4-х выстрелах, считая, что во всех испытаниях вероятность попадания одна и та же.

$$$ 71

Найти вероятность того, что событие наступит не менее двух раз в четырех независимых испытаниях, если вероятность наступления события в одном испытании равна 0,5

$$$ 72

Вероятность появления события в каждом из независимых испытаний равна 0,8. Найти вероятность того, что в 100 испытаниях событие появится не менее 70 и не более 80 раз. Указание

$$$ 73

Вероятность появления события в каждом из 100 независимых испытаниях равна 0,8. Найти вероятность того, что событие появится не менее 75 раз и не более 90 раз. Указание:

$$$ 74

Вероятность появления события в каждом из 100 независимых испытаниях равна 0,8. Найти вероятность того, что событие появится не менее 75 раз. Указание:

$$$ 75

Вероятность появления события в каждом из 100 независимых испытаниях равна 0,8. Найти вероятность того, что событие появится не более 74. Указание:

$$$ 76

Найти вероятность того, что при перевозне 5000 изделий, хотя бы одно изделие повредится, если вероятность повреждения в пути каждого изделия равна 0,0002

$$$ 77

Коммутатор учреждения обслуживает 100 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0,01. Найти вероятность того, что в течение одной минуты никто не позвонит

$$$ 78

Укажите формулу вероятностей для случайной величины имеющей биноминальное распределение с параметрами и , принимающей целочисленные значения от 0 до .

$$$ 79

Укажите формулу вероятностей для случайной величины имеющей геометрическое распределение с параметрами , принимающей целые положительные значения

$$$ 80

Укажите формулу вероятности для случайной величины имеющей распределение Пуассона с параметром , принимающей значения

$$$ 81

Математическим ожиданием дискретной случайной величины , имеющей закон распределения называется число равное

$$$ 82

Математическое ожидание постоянной равно

$$$ 83

Математическое ожидание от произведения постоянной на случайную величину равно

$$$ 84

Математическое ожидание суммы случайных величин равно

$$$ 85

Математическое ожидание отклонения от ее математического ожидания равно

$$$ 86

Математическое ожидание произведения независимых случайных величин равно

$$$ 87

Математическое ожидание биноминальной случайной величины с параметрами и равно

$$$ 88

Укажите формулу для вычисления дисперсии случайной величины

$$$ 89

Число перестановок из элементов равно

$$$ 90

Дисперсия постоянной равна

$$$ 91

Дисперсия произведения постоянной на случайную величину равна

$$$ 92

Дисперсия суммы независимых случайных величин и равна

$$$ 93

Дисперсия суммы постоянной и случайной величины равно

$$$ 94

Дисперсия разности независимых случайных величин и равно

$$$ 95

Дисперсия биноминальной случайной величины с параметрами равна

$$$ 96

Укажите формулу для вычисления среднего квадратического отклонения случайной величины

$$$ 97

Интегральная функция распределения случайной величины определяется равенством

$$$ 98

Пусть интегральная функция распределения вероятностей случайной величины , тогда вероятность того, что значение попадет в промежуток равна

$$$ 99

Для интегральной функции распределения вероятностей случайной величины справедлива

$$$ 100

Вероятность того, что непрерывная величина примет любое фиксированное значение равна

$$$ 101

Пусть - плотность распределения вероятностей непрерывной случайной величины . Тогда вероятность того, что значения величины попадет в промежуток равна

$$$ 102

Для непрерывной величины с плотностью верно

$$$ 103

Пусть - интегральная функция распределения вероятностей случайной величины . Тогда плотность распределения вероятностей определяется равенством

$$$ 104

Интегральная функция распределения вероятностей непрерывной величины , имеющей плотность распределения равна равенством

$$$ 105

Математическим ожиданием непрерывной случайной величины с плотностью называется число равное

$$$ 106

Дисперсией непрерывной случайной величины с плотностью распределения называется число равное

$$$ 107

Укажите формулу плотности распределения вероятностей равномерно распределенной случайной величины на [a,b]

$$$ 108

Укажите формулу плотности распределения вероятностей показательной случайной величины с параметром

$$$ 109

Укажите формулу плотности распределения вероятностей нормальной случайной величины с параметрами и

$$$ 110

Укажите свойство плотности распределения вероятностей

$$$ 111

Вероятность попадания значения нормальной величины с параметрами и в промежуток равна

$$$ 112

Укажите неравенство Чебышева, если - случайная величина, ее математическое ожидание, - дисперсия, - число