Линейная алгебра

$$$ 1

Вычислить

$$$ 2

Вычислить

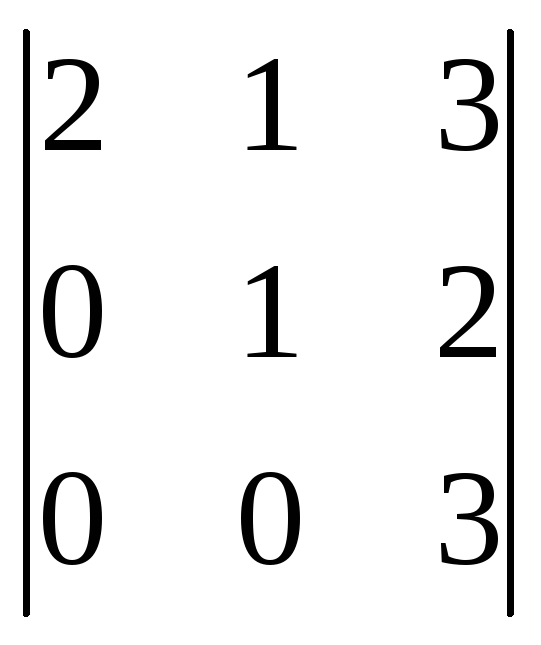
$$$ 3

Вычислить

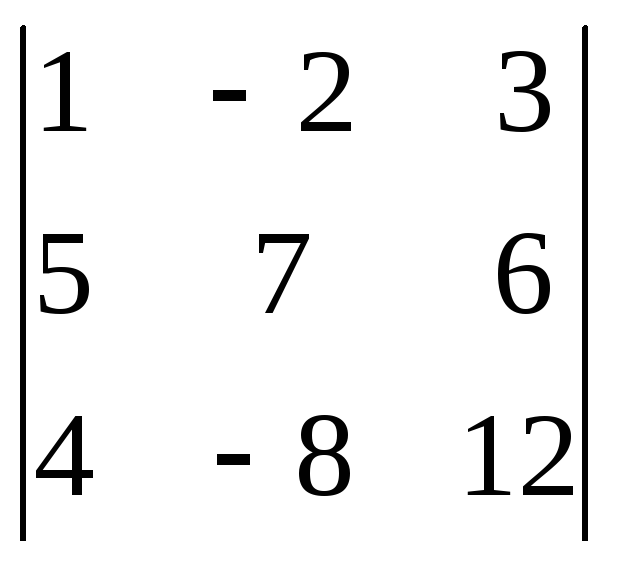
$$$ 4

Решить уравнения:

$$$ 5

Решить уравнения:

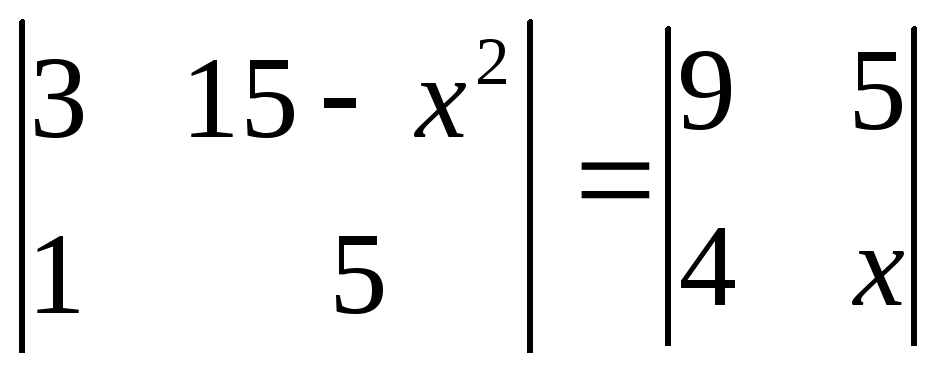
$$$ 6

Решить уравнения:

$$$ 7

Найти алгебраическое дополнение определителя

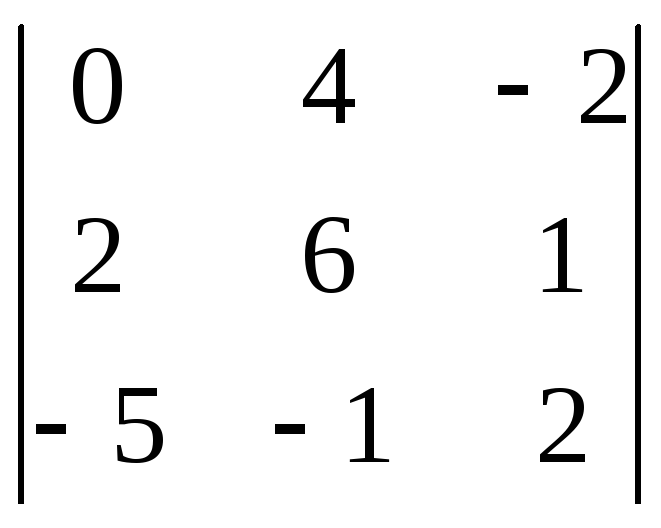
$$$ 8

Найти алгебраическое дополнение определителя

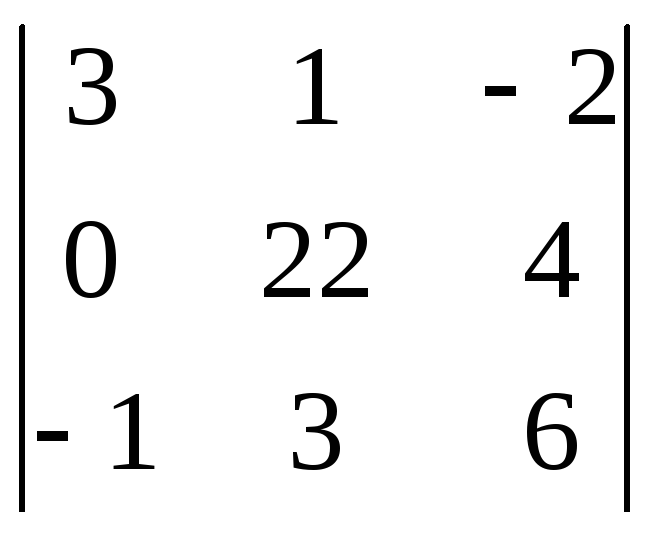
$$$ 9

Найти матрицу , если и

$$$ 10

Найти матрицу , если и

$$$ 11

Найти , если и

$$$ 12

Найти , если и

$$$ 13

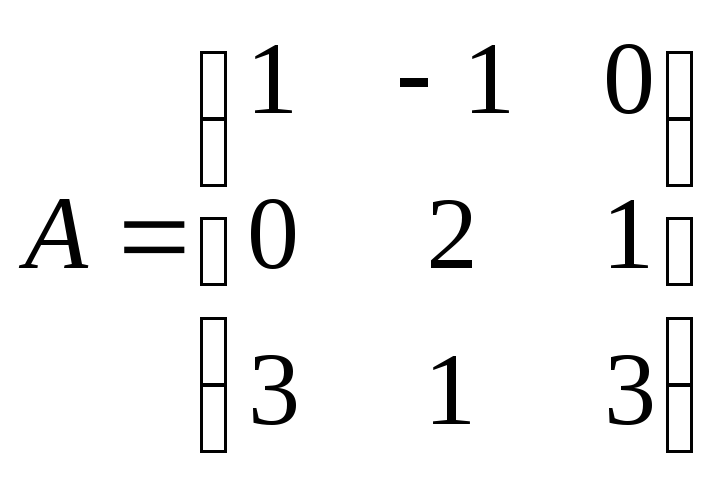Найти , если и

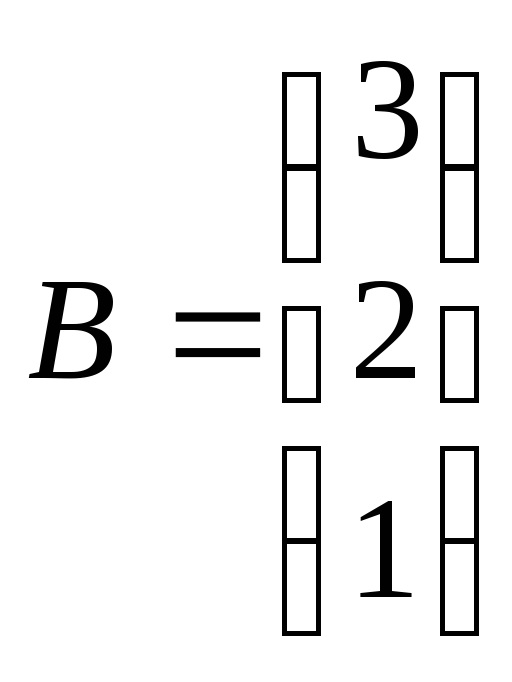
$$$ 14

Решить систему уравнени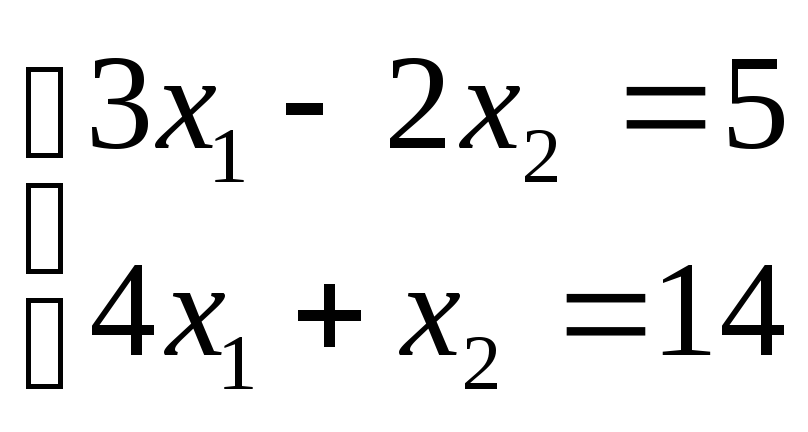й найти

$$$ 15

Решить систему уравнени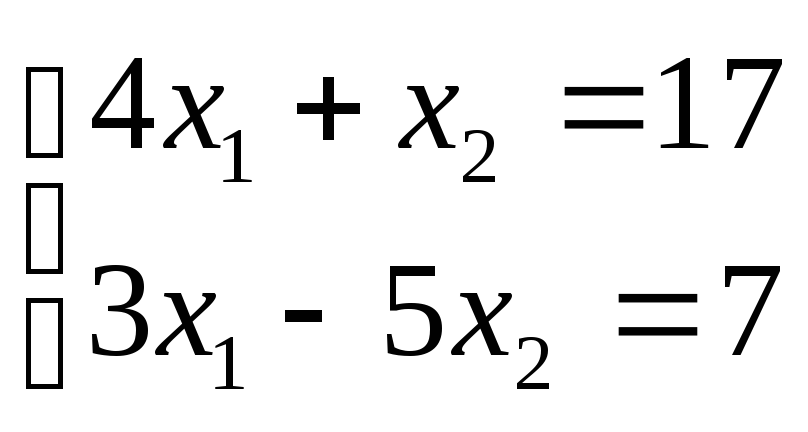й найти

$$$ 16

Решить систему уравнений 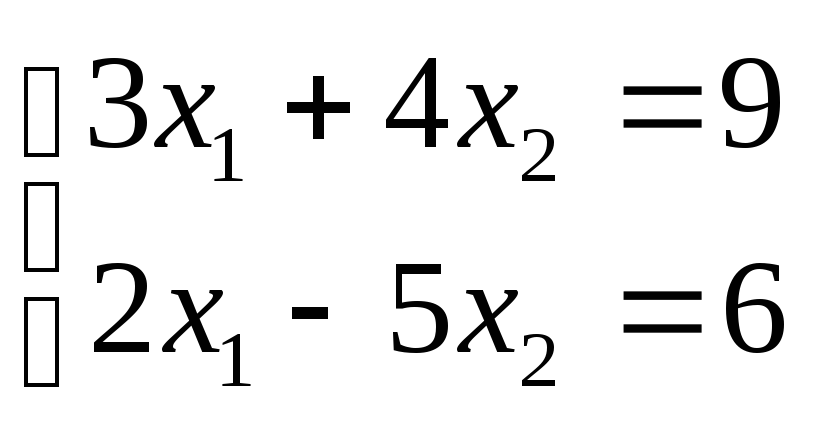и найти

$$$ 17

Решить систему уравнений

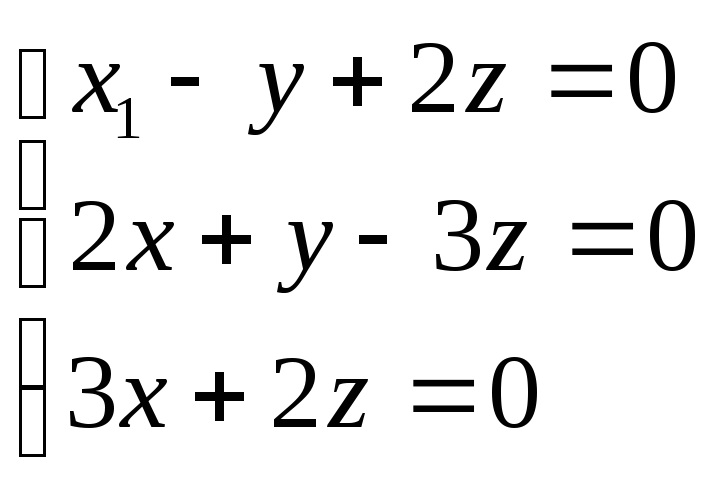
$$$ 18

Для матрицы обратной является

$$$ 19

Для матрицы обратной является:

$$$ 20

Дано . Найти матрицу X

$$$ 21

Решить уравнение

$$$ 22

Определитель третьего порядка 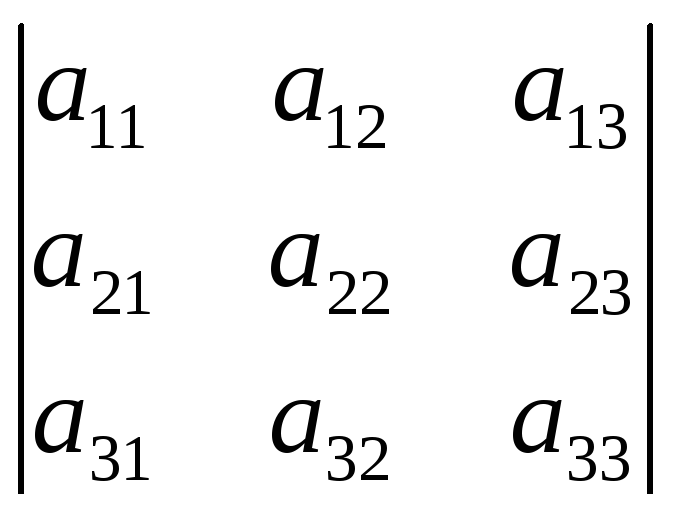равен:

$$$ 23

При перестановке двух строк определитель:

$$$ 24

При умножении какой-либо строки определителя на число значение определителя:

$$$ 25

Если элементы одного столбца определителя соответственно равны элементам другого столбца, то определитель

$$$ 26

При разложении определителя -го порядка по элементам - ой строки его значение равно:

$$$ 27

При разложении определителя - го порядка по элементам -того столбца его значение равно:

$$$ 28

Алгебраическое дополнение элемента равно:

$$$ 29

При умножении матрицы на число :

$$$ 30

Условие, при котором возможна операция умножения матрицы размерности на матрицу размерности :

$$$ 31

Если квадратная матрица имеет обратную, матрицу то:

$$$ 32

Если определитель матрицы 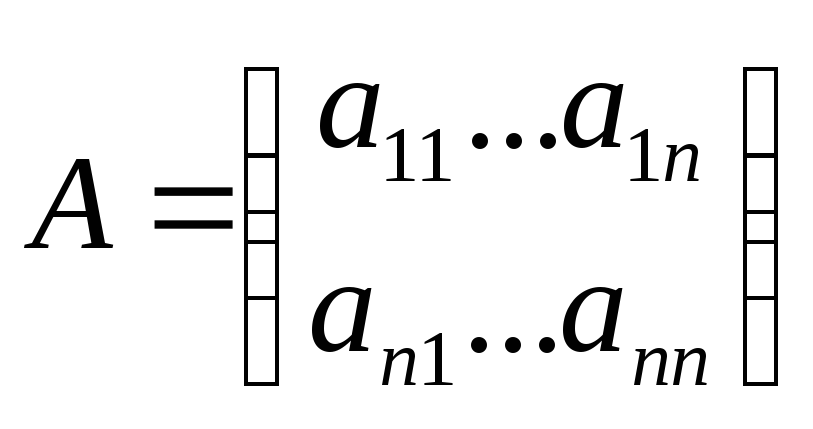не равен нулю, то обратная к вычисляется по формуле

$$$ 33

Если определитель квадратной матрицы не равен нулю, то матрица называется:

$$$ 34

Квадратная матрица называется единичной, если у нее

$$$ 35

Минором элемента определителя называется:

$$$ 36

Матрицы размерности и размерности называются равными, если

$$$ 37

Суммой матриц одинаковой размерности и называется матрица , элементы которой определяются по формуле

$$$ 38

Если определитель системы линейных однородных уравнений с неизвестными не равен нулю, то система

$$$ 39

Система линейных уравнений называется совместной, если она

$$$ 40

Система линейных уравнений называется несовместной, если она

$$$ 41

Для того чтобы система линейных уравнений с неизвестными была совместной, необходимо и достаточно, чтобы

$$$ 42

Формулы Крамера для решения системы - уравнений с n – неизвестными имеют вид:

$$$ 43

Если – основная матрица системы линейных уравнений невырожденная, а – матрица-столбец свободных членов, то решение системы – матрица-столбец неизвестных находится по формуле

Векторное алгебра

$$$ 44

Векторы называются равными, если

$$$ 45

Сумма при и равна

$$$ 46

Векторы и коллинеарны если

$$$ 47

Если векторы и коллинеарны, то найдется число , удовлетворяющее равенству

$$$ 48

Если векторы и образуют на плоскости базис, то на этой плоскости любой вектор можно единственным образом разложить по данному базису

$$$ 49

Векторное произведение векторов и равно:

$$$ 50

Проекция вектора на направленную прямую равна

$$$ 51

Скалярным произведением векторов и называется число

$$$ 52

Скалярное произведение векторов и равно

$$$ 53

Векторы и ортогональны, если

$$$ 54

Указать необходимое и достаточное условие коллинеарности векторов и

$$$ 55

Смешанное произведение векторов , , . равно

$$$ 56

Указать необходимое и достаточное условия компланарности векторов , ,

$$$ 57

Векторным произведением векторов и называется вектор , который удовлетворяет следующим трем условиям:

$$$ 58

Работа произведенная постоянной силой при перемещении тела на пути , определяемом вектором вычисляется по формуле:

$$$ 59

Укажите условие ортогональности векторов и

$$$ 60

Три упородоченных вектора в пространстве образуют базис, если они

$$$ 61

Площадь параллелограмма, построенного на векторах и , имеющих общее начало равна

$$$ 62

Найти скалярное произведение векторов , , если

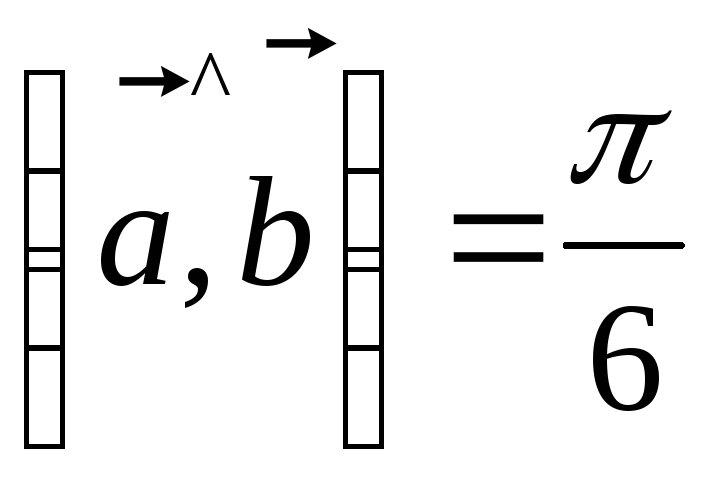
$$$ 63

Найти , если ,

$$$ 64

Найти длину вектора

$$$ 65

Найти направляющие косинусы вектора

$$$ 66

Найти координаты вектора , если ,

$$$ 67

При каком значении вектора и ортогональны

$$$ 68

Найти проекцию вектора на вектор

$$$ 69

Найти , если

$$$ 70

Найти , если для векторов выполняется

$$$ 71

Найти векторное произведение векторов

$$$ 72

Найти векторное произведение коллинеарных векторов и

$$$ 73

Найти площадь параллелограмма, построенного на векторах и , если

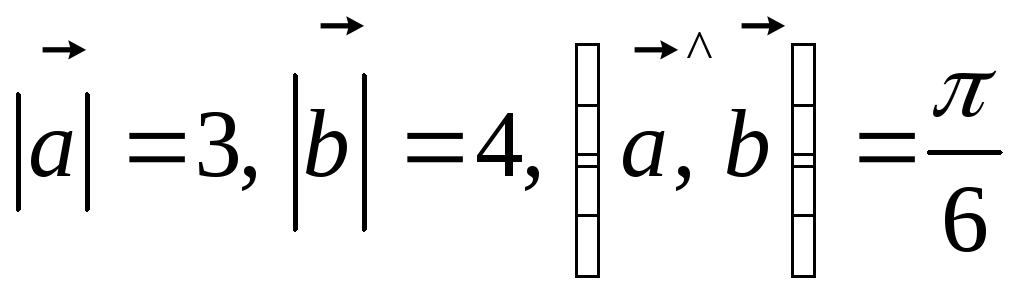
$$$ 74

Найти , если

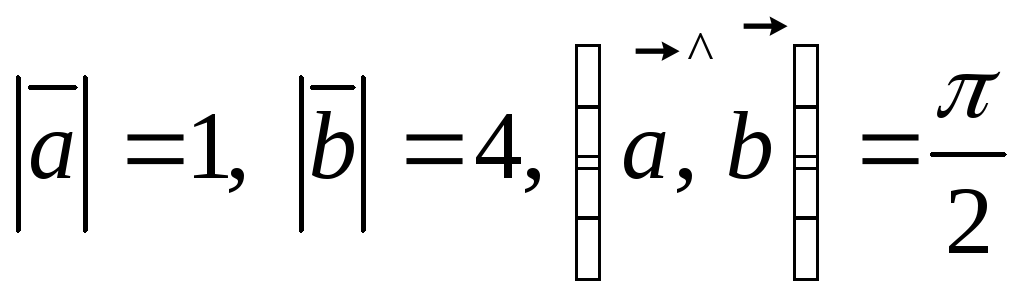
$$$ 75

Найти , если

$$$ 76

Найти объем параллелепипеда построенного на векторах

$$$ 77

Найти , если векторы и ортогональны и

$$$ 78

При каких и векторы и коллинеарны

$$$ 79

Найти длину вектора , если ,

$$$ 80

Чему равен ?

$$$ 81

Чему равна проекция вектора на вектор ?

$$$ 82

Указать необходимое и достаточное условие коллинеарности векторов ,

$$$ 83

При каком значении вектора и перпендикулярны

$$$ 84

Найти , если

$$$ 85

Найти единичный вектор того же направления, что и вектор

$$$ 86

При каком значении векторы и ортогональны

$$$ 87

Найти работу силы при перемещении тела на пути , если

$$$ 88

При каком значении векторы и компланарны?

$$$ 89

Найти смешанное произведение векторов

$$$ 90

Найти , если ,

$$$ 91

Найти если

$$$ 92

Найти , если ,

$$$ 93

Найти , если ,

$$$ 94

Найти координаты вектора , коллинеарного вектору при условии