matematika_1

, где – константа, равен c∫∫df(x,y)dxdy

x-x*2\2+x*3\3…(-1)*n-1 x *n\n+…

Вычислить двойной интеграл , где 1\8

Вычислить двойной интеграл , где 4

Вычислить двойной интеграл , где :1\6

Вычислить двойной интеграл , где :3\20

Вычислить двойной интеграл , где 1\15

Вычислить двойной интеграл , где 10

Вычислить двойной интеграл , где 12

Вычислить двойной интеграл , где 126

Вычислить двойной интеграл , где 2

Вычислить двойной интеграл , где 25

Вычислить интеграл : 4

Вычислить интеграл : 72

Вычислить интеграл : p\4

Вычислить интеграл :1\2

Вычислить интеграл :16\3

Вычислить интеграл :8

Вычислить интеграл :9

Вычислить интеграл: 2

Вычислить интеграл: 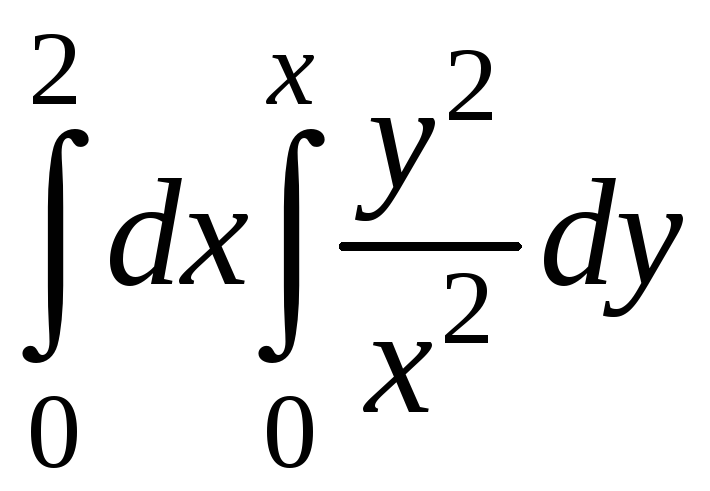2\3

Вычислить интеграл: 4

Вычислить интеграл: 9

Вычислить интеграл: 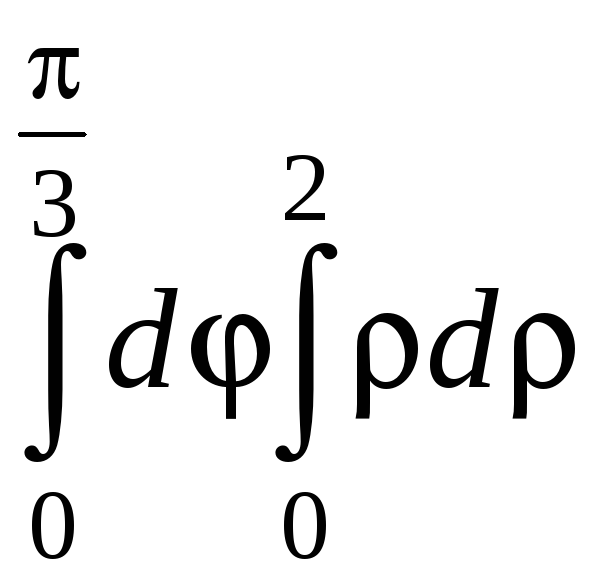2p\3

Вычислить интеграл: 32

Вычислить интеграл: 32

Вычислить интеграл: 4\3

Вычислить интеграл: 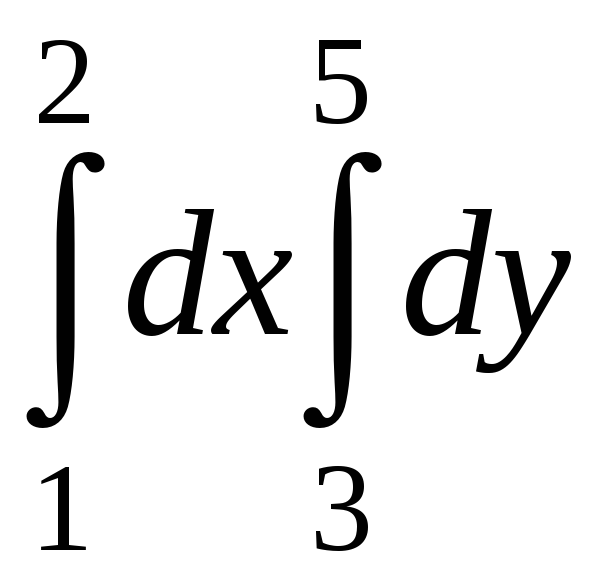2

Вычислить интеграл: 2

Вычислить интеграл: 2

Вычислить интеграл: 26

Вычислить интеграл: 4

Вычислить интеграл: 7

Вычислить интеграл: 8

Вычислить интеграл: 8\3

Вычислить интеграл: p\2

Вычислить интеграл: 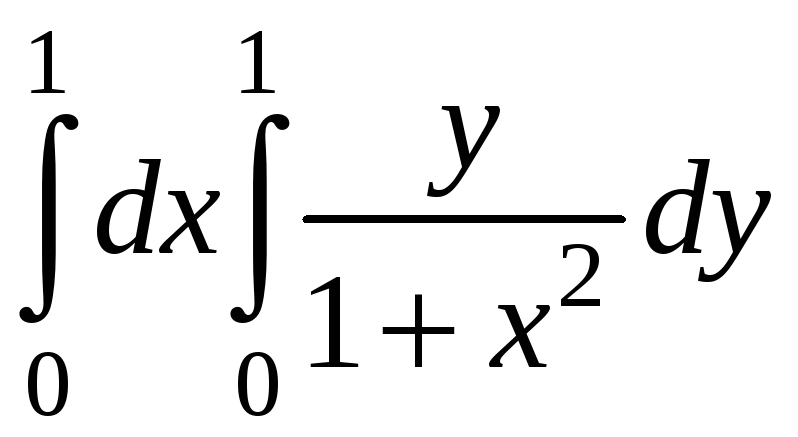p\8

Вычислить интеграл: 9

Вычислить площадь , ограниченной заданным линиями:, , : 1/2

Вычислить площадь , ограниченной заданным линиями:, , : 2

Вычислить площадь , ограниченной заданным линиями:, , : 2

Вычислить площадь плоской фигуры, ограниченной следующими линиями:, , : (6-4ln2)

Гармонический ряд сходится или расходится : расходится

Градиент скалярного поля имеет модуль:

Градиентом функции в данной точке является вектор, координаты которого равны: (2;2)

Градиентом функции в данной точке называется вектор, координаты которого равны соответственно:

Градиентом функции в данной точке является вектор, координаты которого равны: (5;2)

Градиентом функции в данной точке является вектор, координаты которого равны: (3;-1)

Градиентом функции в точке является: (5;-1)

Двойной интеграл равен plowadi d

Дифференциальное уравнение вида или называется: уравнением с разделяющимимся переменными

Дифференциальное уравнение второго порядка вида называется лин однородным с пост коэф

Дифференциальное уравнение второго порядка вида называется: линейным однородным уравнением

Дифференциальное уравнение первого порядка вида , , называется: уравнением Бернулли

Дифференциальное уравнение первого порядка вида называется: линейным уравнением

Дифференциальное уравнение первого порядка вида называется: однородным уравнением

Достаточным условием локального экстремума функции в точке М (необходимое условие экстремума выполняется) является следующее условие: (d*2z\dx*2)m∙(d*2z\dy*2)m-(d*2z\dxdy)m>0, ac-b*2>0

Если – предел функции в точке , то

Если , то дифференциальное уравнение вида называется диф. Уравнениемв полных диф-х

Если в произвести замену переменных: , то Якобиан равен p

Если для числовых рядов и выполняется неравенство , то и сх-ми ∑bn→сх-ть ∑an из расх-ми ∑ an→рас-ть∑bn

Если область интегрирования – прямоугольный параллелепипед, задаваемый неравенствами , то ab∫dx cd∫dy mn∫f(xyz)dz

Если точка – точка возможного экстремума дважды дифференцируемой функции , то она является точкой максимума при условиях: (zxx")n0<o Zxx"(x0y0)<0 ac-b>0

Если точка – точка возможного экстремума дважды дифференцируемой функции , то она является точкой минимума при условиях: Zxx"(x0y0)>0 ac-b⃰2<0

Если характеристические корни линейного однородного дифференциального уравнения с постоянными коэффициентами , действительные и , то общее решение имеет вид y=e⃰kx(c1cosβx+c2cosβx)

Если характеристические корни линейного однородного дифференциального уравнения с постоянными коэффициентами , комплексные и , , то общее решение имеет вид y=e*α(c1+c2∙x)

Если характеристические корни, линейного однородного дифференциального уравнения с постоянными коэффициентами , действительные и , то общее решение имеет вид y=c1e⃰k1xc2e⃰k2x

Записать интеграл в цилиндрических координатах : ∫∫∫v(pcosᶲ,psinᶲ,zpdᶲdpdz

Значение смешанной производной второго порядка функции в точке равно: 14

Значение смешанной производной второго порядка функции в точке равно: 45

Значение частной производной второго порядка функции в точке равно: 24

Значение частной производной второго порядка функции в точке равно: 12

Значение частной производной функции по в точке равно: 2

Значение частной производной функции по в точке равно: 2

Значение частной производной функции по в точке равно: 3

Значе-ние частной производной функции по в точке равно: 3

Изменить порядок интегрирования в повторном интеграле: : 01∫dy -1-√y∫f(x,y)dx

Изменить порядок интегрирования в повторном интеграле: : 01∫dx x*2x∫f(x,y)dy

Изменить порядок интегрирования в повторном интеграле: : 03 ∫dx x3∫ f (x,y)dy

Изменить порядок интегрирования в повторном интеграле: : 03∫dy y3∫(x,y)dx

Изменить порядок интегрирования в повторном интеграле: 01∫dy 3√y1∫ f(x,y)dx

Исследовать на сходимость ряд 1\2<1 сх-ся

Исследовать на сходимость ряд сх-ся

Исследовать на сходимость ряд : ∞ расх-ся

Исследовать на сходимость ряд : расходится

Исследовать на сходимость ряд : расходится

Исследовать сходимость ряда 1\3<1 сх-ся

Исследовать сходимость ряда ∞расх-ся

Исследовать сходимость ряда cх-ся

Исследовать сходимость ряда е<1 расх-ся

Какая формула соответствует понятию полного приращения функции двух переменных:Δz=f(x+Δx, y+Δy)-f(x,y)

Какая формула соответствует понятию частного приращения функции двух переменных по : Δz=f(x,y+Δy)-f(x,y)

Какая формула соответствует понятию частного приращения функции двух переменных по : Δz=(x.y+Δy)-f(x,y)

Масса однородной пластинки выражается формулой ∫∫d dxdy

Найдите 4-й член ряда 1\17

Найдите 4-й член ряда 1\8

Найдите 5-й член ряда

Найти больший корень характеристического уравнения, соответствующего уравнению : -1

Найти область сходимости ряда (-3. 3)

Найти область сходимости ряда │-1\2, 1\2)

Найти область сходимости ряда │-5, 5│

Найти область сходимости ряда -3\2<x<-1\2

Найти область сходимости ряда 4\2<x<5\2

Найти область сходимости ряда (-3 3)

Найти площадь области , ограниченной линиями , , , : 14/3

Найти площадь области , ограниченной линиями , , , : 4/3

Найти площадь области , ограниченной линиями , : 2/3

Найти площадь области , ограниченной линиями , : 32/3

Найти площадь области , ограниченной линиями , : 32/3

Найти площадь области , ограниченной линиями , : 32/3

Найти площадь области , ограниченной линиями , : 4/3

Найти пятый член ряда

Найти радиус сходимости ряда : R=∞

Найти радиус сходимости ряда : 1/6

Найти сумму первых двух членов ряда :19/84

Найти сумму первых двух членов ряда : 9/8

Найти сумму ряда : ∞

Найти сумму ряда : 1/1+x

Найти сумму ряда : 1/1-x

Найти сумму ряда : 3

Найти сумму характеристических корней уравнения : 2.5

Найти четвертый член ряда 1\17

Найти четвертый член ряда 1\8

Найти экстремум функции :Z max=12 в точке М(4;4)

Найти экстремум функции :Z max=9 в точке М(0;3)

Найти экстремум функции :Z min=0 в точке М(1;1/2)

Необходимым условием локального экстремума функции в точке М является: Z'x=0 z'y=0

Областью определения функции является множество точек, удовлетворяющих условию: x-y≠0 y≠x

Областью определения функции является множество точек, удовлетворяющих условию: y≠-x

Областью определения функции является множество точек, удовлетворяющих условию: x-y≥0 y≤x

Определением условной сходимости знакопеременного ряда является ∑│an│-расх-ся a ∑an-ax то ∑an-ax уал

Переход от полярных координат к прямоугольным координатам осуществляется через равенства ( x=pcosᶲ Y=psinᶲ

Полный дифференциал функции равен x\√x⃰2+y⃰2 ax+y\√x*2+y*2 ay

Полный дифференциал функции равен (2xy+y*2)dx+(x*2 2xy)dy

Полный дифференциал функции равен ycosxydx+xcosxydy

Полным дифференциалом функции является выражение: 2xdyx+(x⃰2+2y)dy

Полным дифференциалом функции является выражение:2xdx+2ydy

Полным дифференциалом функции , имеющий непрерывные частные производные, называется выражение: dz=dzdx∕dx+dzdy∕dy

Полным дифференциалом функции является выражение:3x⃰2dx+3y⃰2dy

При каких значениях параметра , ряд сходится

Производная неявной функции при условии , равна: F⃰(x,y)∕F⃰(x,y)

Расставить пределы интегрирования в тройном интеграле , где , , , , : 03∫dx x3∫dy 01∫f (xyz) dz

Решить задачу Коши , y=3+x*2

Решить задачу Коши , , y=2x-sin2x

Решить задачу Коши , , y=2+3e*x