TERVER_13-14

При статистической проверке гипотезы о равенстве генеральных средних, в случае, когда генеральные дисперсии известны, используется случайная величина, имеющая распределение

—Фишера-Снедекора (F)

—нормальное(Z)

—Стьюдента(Т)

—Пирсона

При статистической проверке гипотезы о равенстве генеральной средней стандарту (генеральная дисперсия неизвестна) в качестве критерия используется случайная величина, имеющая распределение

—Стьюдента (Т)

—нормальное (Z)

—Фишера-Снедекора (F)

—Пирсона

При статистической проверке гипотезы о равенстве генеральной средней стандарту (генеральная дисперсия известна) в качестве критерия используется случайная величина, имеющая распределение

—нормальное (Z)

—Фишера-Снедекора (F)

—Пирсона

—Стьюдента (Т)

При статистической проверке гипотезы о равенстве генеральных средних (генеральные дисперсии неизвестны, но равны) в качестве критерия используется случайная величина, имеющая распределение

—Пирсона

—нормальное (Z)

—Стьюдента (Т)

—Фишера-Снедекора (F)

Правильная форма нулевой гипотезы H 0 имеет вид

—H0 : x a

—H0 : x a

—H0 : x a

—H0 : x a

Альтернативная гипотеза имеет вид H1 : x1 x2 . Критическая область

—правосторонняя

—произвольная

—левосторонняя

—двусторонняя

Границей между критической областью и областью принятия нулевой гипотезы является

—прямая

—окружность

—точка

—парабола

средних в конкурирующей гипотезе должен быть знак —> или

—< или ≠

—только ≠

—только <

Альтернативная гипотеза имеет вид H1 : x a . Критическая область

—правосторонняя

—двусторонняя

—произвольная

—левосторонняя

Исправленная выборочная дисперсия определяется по формуле

Наблюдаемое значение критерия Фишера-Снедекора равно

—S м2

Sб2

—S12 S22

—Sб2

Sм2

—S1 S 2

Наблюдаемое значение критерия Z при проверке гипотезы о равенстве генеральной средней стандарту (D(X) известна) определяется формулой

— x 2 a D X

—x a D( X )

n

— x2

a D( X ) n

D( X )

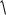— ~ n

x a

~ ~ x1 x2

—D( X1 ) D( X 2 )

n1 n2

~ ~

—x1 x2

D( X1 ) D( X 2 ) n1 n2

Наблюдаемое значение критерия Стьюдента (проверка гипотезы о равенстве

Наблюдаемое значение критерия Стьюдента при проверке гипотезы о значимости выборочного коэффициента корреляции определяется по формуле

—rвыб

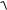1 rвыб2

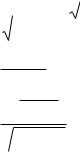
—rвыб

1- rвыб

—n 2

1 rвыб2

Наблюдаемое значение критерия Фишера-Снедекора равно отношению

—выборочных дисперсий

—квадратов выборочных дисперсий

—квадратов исправленных выборочных дисперсий

—исправленных выборочных дисперсий

Если число вариант нормального распределения выборки l = 15, а s число параметров этого распределения, то число степеней свободы k критерия согласия 2 Пирсона равно

—16

—12

—14

—15

Тема 10. Корреляционно-регрессионный анализ

Уравнение регрессии отыскивается

—выборочным методом

—методом интегрированием по частям

—методом наименьших квадратов

—методом множителей Лагранжа

Корреляционной зависимостью называется статистическая зависимость, при которой каждому значению случайной величины Х ставится в соответствие

—определенное значение случайной величины Y

—распределение случайной величины Y

—корреляционное отношение

—числовая характеристика соответствующего распределения случайной величины Y

Коэффициент а в уравнении регрессии yx ax b показывает

—тесноту связи между факторным и результативным признаками

—на сколько единиц изменится значение результативного признака при изменении факторного признака на 1 единицу

—на сколько процентов изменится значение результативного признака

—изменение факторного признака

Если при равномерном возрастании значений факторного признака средние значения результативного признака равномерно возрастают, то уравнение регрессии отыскивается в виде

—линейного уравнения

—уравнения гиперболы

—уравнения параболы

—уравнения третьей степени

Если при равномерном возрастании значений факторного признака средние значения результативного признака неравномерно убывают, то уравнение регрессии отыскивается в виде

—линейного уравнения

—уравнения гиперболы

—уравнения параболы

—уравнение третьей степени

Универсальным показателем тесноты связи между факторным и результативным признаками является

—уравнение регрессии

—корреляционное отношение

—факторная дисперсия результативного признака

—остаточная дисперсия результативного признака

Корреляционное отношение отыскивается по формуле

Cвязь между факторным и результативным признаками является тесной, если

— 1

— 0

— 1

—

Линейный коэффициент корреляции определяется формулой

—r ax b

x y

—r x y xy x y

—r xy x y

x y

В случае линейного уравнения регрессии связь между факторным и результативным признаками является тесной, если

—r 1

—r 0

—r 1

—r 1

Общая дисперсия результативного признака – это мера колеблемости результативного признака под воздействием

—только факторного признака

—только случайных факторов

—всех факторов, влияющих на изменение результативного признака

—общего признака

Остаточная дисперсия результативного признака – это мера колеблемости признака под воздействием

—только факторного признака

—только случайных факторов

—всех факторов, влияющих на изменение результативного признака

—общего признака

Cтатистической называется зависимость, при которой каждому значению случайной величины Х соответствует

—определенное значение случайной величины Y

—произвольное значение случайной величины Y

—распределение случайной величиныY

—постоянная величина величина Y

Корреляционная зависимость называется регрессионной, если каждому значению случайной величины X соответствует

—средняя величина распределения случайной величины Y

—дисперсия случайной величины Y

—среднее квадратическое отклонение случайной величины Y

—определенное значение случайной величины Y

Парная корреляция – это зависимость, при которой результативный признак Y зависит от

—двух факторных признаков

—множества факторных признаков

—совокупности пар (xi ; yi )

—одного факторного признака Х

Задачей регрессионного анализа является

—определение формы связи между факторным и результативным признаками

—установление тесноты связи между факторным и результативным признаками

—вычисление ошибки показателя тесноты связи

—определение доверительного интервала для показателя тесноты связи

Если связь между факторным признаком и средним значением результативного признака – линейная, то

—r

—r

—r

—r

Линейный коэффициент корреляции определяет тесноту связи между признаками Х и Y, если связь

—линейная

—дробно-линейная

—гиперболическая

—квадратичная

Корреляционная связь тем теснее, чем меньше рассеяние между результативным Y и факторным Х признаками под влиянием

—учтенных факторов

—неучтенных факторов

—всех факторов

—изучаемого факторного признака

Если влияние фактора Х мало осложняется действием других факторов, то зависимость между Y и Х является

—слабой

—случайной

—тесной

—остаточной

Определение зависимости по наблюдаемым значениям xi и yi называется

—выравниванием эмпирических данных

—выпрямлением эмпирических данных

—осреднением эмпирических данных

—рассеянием эмпирических данных

Согласно методу наименьших квадратов наилучшей аппроксимирующей кривой будет та, для которой

—среднее отклонение ординат эмпирических точек от выравненных будет минимальным

—квадрат среднего отклонения ординат эмпирических точек от выравненных будет минимальным

—сумма отклонений ординат эмпирических точек от выравненных будет минимальной

—сумма квадратов отклонений ординат эмпирических точек от выравненных будет минимальной

Уравнение, связывающее условную среднюю yxi со значением факторного признака

xi , называется

—уравнением регрессии

—уравнением тесноты связи

—гипотетическим уравнением

—корреляционным уравнением

Корреляционном полем переменных (х,у) называется

—совокупность точек (хi ,уi) на координатной плоскости

—изображение линий, на которой обозначены точки (хi,уi)

—таблица, в которой даны значения ( xi + yi )

Теснота связи это

—отношение суммы значений yi к сумме значений xi

—производная Y по X

—мера рассеяния результативного признака Y около линии регрессии

—мера рассеяния факторного признака Х около уравнения регрессии

Значения линейного коэффициента корреляции принадлежат промежутку

—0; )

—0;1

—0;2

—1;1

Значения корреляционного отношения принадлежат промежутку

—0; )

—0;1

—0;2

—1;1

Множественная корреляция это зависимость

—когда одному значению x соответствует множество значений yi

—зависимость результативного признака от двух и более факторных признаков

—совокупность пар (хi ,уi)

—криволинейная зависимость между X и Y

Корреляционный анализ определяет

—форму связи между X и Y

—производную Yx

—тесноту связи между X и Y

— xdx ydy

Линия, построенная по наблюдаемым значениям xi и yi называется

—теоретической

—выравнивающей

—эмпирической

—наблюдаемой

Система уравнений для определения коэффициентов уравнения регрессии называется системой

—параметрических уравнений

—нелинейных уравнений

—функциональных уравнений

—нормальных уравнений

Корреляционный метод может быть применен, если число наблюдений

—мало

—достаточно велико

—равно 5

—равно числу наблюдаемых значений xi

Определение тесноты связи между факторным Х и результативным Y признаками – это задача

—регрессионного анализа

—выборочного метода

—корреляционного анализа

—метода наименьших квадратов

Уравнение регрессии связывает значения факторного признака xi с

—определенным значением результативного признака

—максимальным значением результативного признака

—средним значением результативного признака

—дисперсией результативного признака

Линия, построенная по уравнению регрессии, называется

—эмпирической

—наблюдаемой

—выпрямляющей

—выравнивающей

В уравнении регрессии y x ax b коэффициент а равен

—xy x y y 2 ( y)2

—xy x y

x y

—xy x y x 2 (x)2

—x 2 (x)2

xy x y

Дисперсия факторного признака x 2 равна

—x2 (x)2

—x2 (x)2

—(x)2 x2

—xy x y

Зависимость средней выработки одного рабочего за смену Y(шт) от квалификации Х (разряды) приведена в таблице:

Уравнение регрессии y x ax b . Коэффициент a равен

—2,8

—5,3

—5,8

—7,2

Зависимость спроса на данный товар Y (тыс. шт.) от средних доходов населения Х (тыс. руб.) приведена в таблице:

Уравнение регрессии y x ax b . Коэффициент a равен

—1,2

—2,6

—4,4

—5,8