
- •Оглавление
- •Структуры данных и эффективность алгоритмов.
- •Построение модели задачи. Процедурная абстракция и абстракция данных.
- •Основы анализа алгоритмов. [4 ч.1, гл.17, гл.34.]
- •Наихудшее и среднее время работы.
- •Пример 4. Рассмотрим вычисление полинома
- •Асимптотические обозначения.
- •Сложность задач и нижние оценки.
- •Труднорешаемые задачи и np-полнота. [8, 4 гл.34.]
- •Типы данных и структуры данных.
- •Абстрактные типы данных.
- •Последовательность (Sequence). [13 гл.4,5,11.1; 7 п.2.1-4; 3 гл.3-4; 4 п.10.1-3.]
- •Множество (Set). [7 гл.4.1-4; 13 п.10.2; 2 гл.4.]
- •Словарь (Dictionary, Map), другое название – ассоциативный массив [7 п.4.5-8; 3 гл.12; 2 п.4.10; 13 гл.8.].
- •Очередь с приоритетом (Priority queue). [7 п.4.10-11, п.5.6; 3 гл.9; 4 п.6.5; 2 п.4.10-13; 13 гл.7.]
- •Непересекающиеся множества (Disjoint Sets, Partitions, Разбиения) [7 п.5.5; 4 гл.21; 2 п.4.6-8.].
- •Деревья, графы и отношения общего вида. [13 гл.6,12; 7 гл.3, п.4.12, гл.6-7; 3 гл.17.]
- •Структуры данных как способы представления атд.
- •Линейные структуры данных.
- •Деревья.
- •Поисковые деревья (search tree). [13 гл.9]
- •Splay-дерево [19 п.4.3; 3 п.13.2]
- •Деревья цифрового (позиционного) поиска (DigitalSearchTrees,TrieTrees).[7 п.5.3; 3 гл.15.; 13 п.11.3]
- •Пирамиды (heap), другое название – сортирующее (или частично упорядоченное) дерево. [4 гл.6,19-20]
- •Структуры данных для непересекающихся множеств (отношения эквивалентности). [4 гл.21]
- •Рандомизированные структуры данных.
- •Случайная балансировка бинарных поисковых деревьев. [3 п.13.1]
- •Списки пропусков (Skip Lists). [13 п.8.6; 3 п.13.5]
- •Декартово дерево (Treap). [4 гл.13 Задачи 13-4; 20]
Splay-дерево [19 п.4.3; 3 п.13.2]
Специфическая структура данных – Splay-дерево. Это бинарное дерево поиска, но при этом не поддерживается явного баланса, оно может оказаться разбалансированным в определенном (традиционном) смысле. Вместо этого после выполнения каждой операции, типовой для бинарных поисковых деревьев, осуществляется перестройка (сохраняющая определяющие свойства поискового дерева) с целью «подтянуть» вершины текущего пути дерева поближе к корню, что ускоряет их нахождение в будущем. Для такого представления вышеупомянутые операции с множествами (и некоторый набор дополнительных операций) имеют время работы O(log(n)), но амортизированное.
Перестройка проводится с помощь трех Splay-операций:
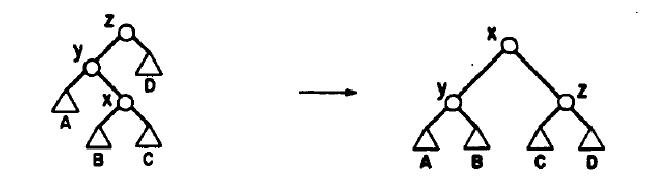
Zig: Если родитель вершины x является корнем:

Zig-Zig: Если родитель вершины x не является корнем, но x и его родитель либо оба левые либо оба правые сыновья:

Zig-Zag: Если родитель вершины x не является корнем, но x – левый сын, а его родитель – правый сын:
Возможности организовать балансировку расширяются, если допускать изменение количества сыновей вершины в фиксированном диапазоне [k,m]. К таким методам балансировки относятся 2-3-деревья, В-деревья и их вариации. Сильно ветвящиеся В-деревья представляют особый интерес при работе с данными, хранящимися во внешней памяти.
Баланс в АВЛ деревьях и красно-черных деревьях поддерживается за счет операций вращения. Из-за сложности операций балансировки считается, что сбалансированные деревья следует использовать лишь в том случае, когда поиск информации производится значительно чаще, чем включение. Можно предложить другую модель кодирования словаря, в которой все листья дерева расположены на одном и том-же уровне, а степень ветвления вершин может быть более двух. Баланс в таких деревьях поддерживается за счет изменений степеней вершин.
Существует множество других операций над сбалансированными деревьями, которые поддерживают их сбалансированность. Сбалансированные деревья используются и для представления последовательностей таким образом, что можно будет быстро вставлять элементы в последовательность, преодолевая трудности, которые связаны с последовательным расположением элементов (в массиве), и обеспечивая при этом произвольный доступ к элементам последовательности, т. е. преодолевая сложности связанного размещения элементов. При этом такие представления позволяют эффективно реализовать операции сцепить (конкатенация) и расцепить для последовательностей.
Исследуются и известны расширения выше отмеченных структур данных предназначенные для применения в различных предметных областях, естественно имеющих свою специфику интерпретации данных. Например, расширение красно-черных деревьев для работы с ключами вида интервал вещественных чисел [4 п.14.3], которое представляет прямой интерес в задачах вычислительной геометрии.
Деревья цифрового (позиционного) поиска (DigitalSearchTrees,TrieTrees).[7 п.5.3; 3 гл.15.; 13 п.11.3]
В задачах поиска зачастую ключ поиска представлен последовательностью в (достаточно ограниченном) конечном алфавите (цифр или букв). В частности, при желании любой ключ можно трактовать как двоичную (или 16-ю) последовательность.
Такое позиционное представление ключа эффективно используется в алгоритмах позиционной сортировки (сегментная-поразрядная сортировка, bucket- radix sort). Если длина ключа и размер алфавита ограничены сверху константой, то можно отказаться от сравнения ключей (на меньше-больше), и упорядочивать множество с такими ключами за линейное время (с мультипликативной константой, зависящей от размера алфавита и длины ключа). См. [7 п.8.5; 4 гл.8; 3 гл.10.], а также Пример 2. Лексикографическая сортировка.
В дереве цифрового поиска разветвления основаны не на полном сравнении ключей, а на значении очередной позиции ключа. Такие деревья широко используются в задачах обработки текстов, а точнее для хранения и поиска слов (и текстов) в поисковых словарях:
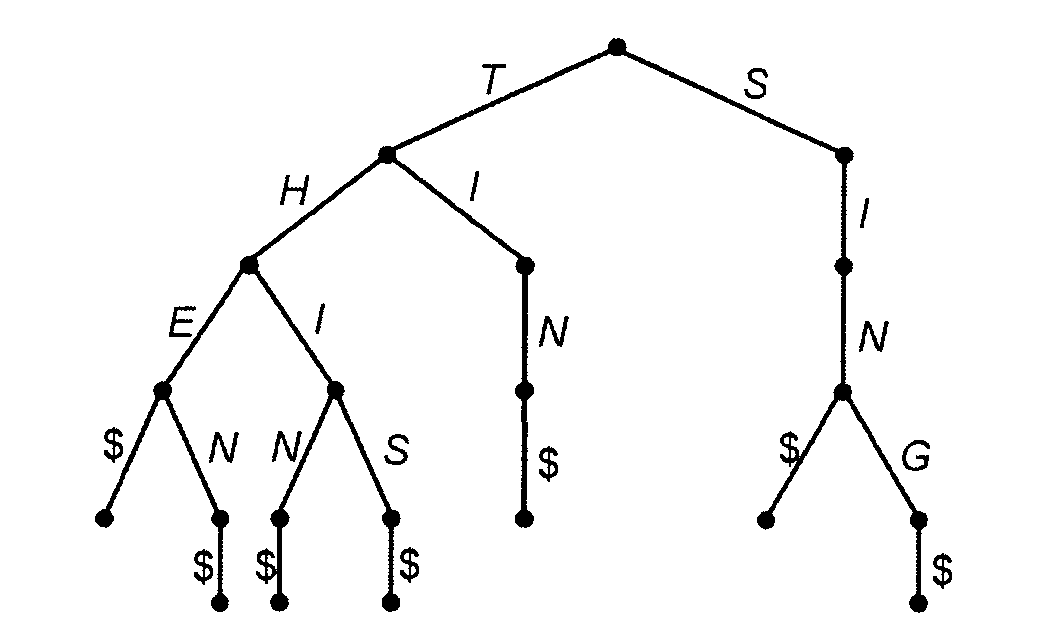
Это дерево хранит множество слов (ключей поиска) {THE, THEN, THIN, THIS, TIN, SIN, SING}. Корень соответствует пустой строке,а два его сына - префиксам Т и S. Самый левый лист представляет слово THE, следующий лист - слово THEN и т.д.
Для деревьев цифрового поиска временные характеристики основных операций аналогичны таковым для бинарного поискового дерева, т.е. O(log(n)) в среднем, но в худшем случае не превышает количества позиций в искомом ключе.
Для задач обработки текстов (в частности задачи поиска по ключевым словам с точным и неточным сопоставлением) на основе деревьев цифрового поиска разработаны более сложные структуры данных (например, суффиксные деревья), позволяющие эффективно решать эти задачи [2 п.9.5; 15; 16].
