2.3.2. Локальная форма закона сохранения импульса

Аналогично законам сохранения массы и энергии можно получить локальную (для отдельной точки пространства) форму закона сохранения импульса.

Отличие будет заключаться лишь в векторной природе переносимой субстанции импульса единичного объема:

, (2.54)

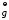
где ускорение, приобретаемое системой за счет действия массовых сил. Массовой силой, действующей на систему, является сила тяжести, соответственно, гдеускорение свободного падения. При вращательном движении возникнет еще одна силацентробежная. Однако способ ее учета в уравнении движения (2.54) будет зависеть от выбора системы отсчета. Если лабораторная система отсчета связана с аппаратом, который вращается вместе со средой, то центробежная сила учитывается как массовая и. Если же лабораторная система отсчета связана с Землей и вращение происходит относительно нее, то вводить центробежную силу дополнительно не следует, она автоматически появится при записи конвективных членов уравнения движения (см., например, в приложении П.2.2 уравнение движения, где).

Разделив тензор потока импульса на конвективную часть и тензор вязких напряжений (1.49), можно представить общий вид уравнения движения с использованием субстанциональной производной:

. (2.55)

Допустив постоянство плотности и коэффициента молекулярной вязкости, получим для ламинарного движения уравнение Навье-Стокса:

, (2.56)

где . (2.57)

Поскольку уравнение (2.56) является векторным, оно может быть представлено в виде трех уравнений для всех координат. Можно поделить на плотность каждый из членов уравнения (2.56), тогда

. (2.58)

Рассмотрим частные случаи уравнения Навье-Стокса. Для идеальной среды, движущейся без трения (=0), оно переходит в уравнение движения Эйлера:

, (2.59)

а для покоящейся среды вуравнение равновесия Эйлера

. (2.60)

Решая уравнение движения совместно с уравнением неразрывности и условиями однозначности, можно получить поля давления, скорости и потока импульса в аппарате. К сожалению, система уравнений (2.55) и (2.16) не имеет общего аналитического решения. Получены решения лишь для частных простейших случаев. Кроме того, возможно численное решение этой системы дифференциальных уравнений с использованием компьютеров. Однако это требует больших затрат машинного времени и затрудняет теоретический подход к проектированию аппаратов.

2.4. Исчерпывающее описание процессов переноса

Дифференциальные уравнения второго порядка с частными производными, полученные на основе уравнений переноса и законов сохранения массы, импульса и энергии (2.16), (2.27), (2.45), (2.55) или их частные случаи, а также условия однозначности к ним, составляют «исчерпывающее математическое описание процессов переноса» [17] (без учета переноса энергии посредством излучения). Оно в принципе позволяет решить как прямую задачу поверочного расчета любого аппарата, т.е. зная конструкцию и размеры аппарата, находить поля скорости, давления, температуры и концентраций в нем; так и обратную задачу проектного расчета определять размеры аппарата по требуемым значениям перечисленных выше величин на входе и выходе из него. Проблема заключается лишь в математической сложности решения этих задач.