2.2.2. Локальная форма закона сохранения энергии

Аналогично тому, как в разд. 2.1 получили уравнение сохранения массы в локальной форме, т.е. для отдельной точки в пространстве, можно получить и локальное уравнение сохранения энергии. Применительно к единичному объему его можно сформулировать следующим образом:

Переносимой субстанцией является энергия единичного объема :

. (2.43)

На практике при рассмотрении процесса переноса тепла в изобарных условиях можно пренебречь работой по преодолению сил трения и изменением механической энергии, тогда можно записать локальный аналог уравнения (2.40):

. (2.44)

В этом случае можно рассматривать как поток тепла, заменив в уравнении (1.42)на. Используя соотношение, связывающее энтальпию с изобарной теплоемкостью и температурой, а также и выражение для потока тепла, можно записать уравнение нестационарной конвективной теплопроводности:

. (2.45)

Как и в (2.25), в многофазных системах перенос тепла из одной фазы в другую может учитываться с помощью дополнительного слагаемого в уравнении (2.45) источника теплаr_q, с помощью его также можно учесть тепловые эффекты химических реакций.

В частном случае ламинарного движения и постоянства теплофизических характеристик с_р, = const, =0 уравнение (2.45) преобразуется в уравнение Фурье-Кирхгофа:

, (2.46)

где -коэффициент молекулярной температуропроводности, м²/с.

При теплопереносе в неподвижной среде получим уравнение нестационарной теплопроводности Фурье:

. (2.47)

При стационарном переносе тепла предыдущее уравнение еще более упрощается:

. (2.48)

Решение дифференциальных уравнений, полученных на основе закона сохранения и уравнения переноса энергии, совместно с условиями однозначности позволяет получить поля температуры и потока тепла в аппарате.

2.3. Закон сохранения импульса

Суть закона сохранения импульса состоит в том, что суммарный импульс изолированной системы есть величина постоянная ,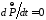. Если же система находится под воздействием внешних сил, то производная от импульса системы по времени равна результирующей силе, действующей на систему.

2.3.1. Интегральная форма закона сохранения импульса

По аналогии с законом сохранения массы отдельного компонента для неизолированной системы можно сформулировать и закон сохранения импульса: изменение импульса в фиксированном объеме V вызывается разностью прихода и отвода импульса из выделенного объема, а также источником импульса. Отличие состоит в том, что импульс является векторной величиной.

, (2.49)

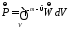, (2.50)

где импульс среды в выделенном объеме;,приход и отвод импульса из объемаза время t; количество импульса, образующегося в единице объема за единицу времени (источник импульса).

В соответствии со вторым законом Ньютона источником импульса являются силы, действующие на систему:

. (2.51)

С учетом этого для непрерывных процессов уравнение (2.49) можно представить в следующем виде:

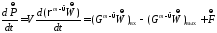. (2.52)

В качестве сил, действующих на движущуюся среду, могут рассматриваться силы давления и тяжести. В частном случае, когда суммарным действием всех сил можно пренебречь , и процесс протекает в стационарных условиях , тогда

. (2.53)