Глава 2. Законы сохранения

При анализе технологических процессов и расчете аппаратов используются законы сохранения массы, импульса и энергии. Следует напомнить, что эти фундаментальные законы сформулированы на основе многочисленного экспериментального материала, а также могут рассматриваться как появление однородности пространства и времени. Релятивистские эффекты взаимосвязи массы и энергии в химической технологии, как правило, пренебрежимо малы. Законы сохранения могут записываться применительно как ко всей системе или ее частям (интегральная форма), так и к отдельным точкам пространства (локальная форма), использоваться для среды в целом или отдельных компонентов.

2.1. Закон сохранения массы

Суть закона сохранения массы заключается в том, что масса не может исчезать либо возникать, т.е. суммарное количество массы в закрытой системе неизменно (закрытая система не обменивается массой с окружающей средой), следовательно, М = 0 или dM/dt = 0. Рассмотрим закон сохранения массы для открытых систем.

2.1.1. Интегральная форма закона сохранения массы (материальный баланс)

Изменение массы в некотором фиксированном объеме V вызывается разностью прихода и отвода массы из выделенного объема:

, (2.1)

где изменение плотности.

Зачастую при описании непрерывных процессов удобнее пользоваться понятием массового расхода G, который является количеством массы, прошедшим за единицу времени. Отнесем величины, входящие в уравнение (2.1), к бесконечно малому промежутку времени:

. (2.2)

Если плотность вещества не меняется (среда несжимаемая) или процесс протекает в стационарных условиях, то материальный баланс упрощается:

. (2.3)

Можно записать уравнение материального баланса для каждого компонента:

. (2.4)

Данное уравнение не является универсальным и справедливо лишь при отсутствии химических реакций в системе, так как в последнем случае одни компоненты могут переходить в другие. В общем случае уравнение материального баланса для каждого компонента будет иметь вид

, (2.5)

где масса компонентаi, образующаяся в единице объема за единицу времени (источник массы). Просуммировав уравнения (2.5) по всем компонентам, мы должны получить уравнение (2.1) для всей массы в целом. Отсюда вытекает естественное условие на источники массы отдельных компонентов (отрицательные источники массы иногда называют стоками):

. (2.6)

Можно переписать уравнение (2.5) в терминах расходов:

. (2.7)

2.1.2. Локальная форма закона сохранения массы (уравнение неразрывности)

В локальной форме закон сохранения массы может быть сформулирован аналогично материальному балансу. Отличие заключается лишь в том, что в данном случае рассматривается не конечный объем V, а бесконечно малый dV. Получим математическую формулировку закона в такой форме. Отметим, что речь идет не о выводе закона, а о получении одного из вариантов его математической записи.

Рассмотрим движение среды как целого через элементарный фиксированный объем . При прохождении через данный объем возможно изменение массового потока, обусловленное изменением скоростии плотностисреды. Только использование среднемассовой скорости позволяет записать суммарный поток массы всех компонентов в лабораторной системе отсчета при наличии градиентов концентраций в виде произведения . Для краткости записи в дальнейшем не будем указывать, функциями каких переменных являются макроскопические величины.

Рис. 2.1. Изменение массового потока, направленного вдоль оси x и проходящего через элементарный объем dV

Массовый расход среды, входящий в объем dV через грань, перпендикулярную оси x, будет равен

, (2.8)

а выходящий можно представить как

. (2.9)

Изменение расхода вдоль оси x:

. (2.10)

Аналогичным образом можно рассмотреть изменения массового расхода вдоль осей y и z:

, (2.11)

. (2.12)

Суммарное изменение расхода в объеме dV равно сумме изменений по всем трем осям:

. (2.13)

Применим к рассматриваемому объему dV уравнение материального баланса (2.2), используя в нем частную производную от плотности по времени с учетом того, что плотность зависит еще и от пространственных координат:

. (2.14)

Решая совместно уравнения (2.13) и (2.14), получим

. (2.15)

Используя дифференциальный оператор , а также выражение для потока массы, эту запись можно представить в виде

. (2.16)

Данное уравнение, выражающее в локальной форме закон сохранения массы, носит название уравнения неразрывности. Левая часть этого уравнения характеризует изменение во времени плотности движущейся среды в фиксированной точке пространства (элементарном объеме dV), неподвижной относительно лабораторной системы отсчета.

Зачастую интерес представляет изменение плотности во времени в точке, движущейся вместе со средой, т.е. со скоростью . Для этого необходимо использовать полную производную по времени:

. (2.17)

Учитывая, что производные от пространственных координат по времени дают соответствующие проекции вектора скорости, можно переписать

. (2.18)

Такая полная производная по времени от величин, зависящих также от пространственных координат, носит название субстанциональной производной, обозначается и характеризует изменение величины во времени для наблюдателя, движущегося вместе со средой со скоростью. Рассмотрим частный случай установившегося (стационарного) движения, при этом в каждой точке пространства, фиксированной относительно лабораторной системы отсчета, плотность со временем меняться не будет (). Однако плотность может меняться в пространстве, тогда для движущегося вместе с потоком наблюдателя она со временем будет изменяться () по (2.18). Первый член этого уравнения характеризует локальное изменение величины, а последующие три конвективное.

Уравнение неразрывности можно записать с использованием субстанциональной производной. Распишем правую часть уравнения (2.16) как производную от произведения двух функций и перенесем конвективный член в левую часть:

, (2.19)

. (2.20)

Левая часть уравнения (2.20) есть в соответствии с (2.18) субстанциональная производная, тогда

. (2.21)

Выбор того или иного способа записи уравнения неразрывности (2.16) или (2.21) определяется удобством использования при решении конкретных задач. Рассмотрим частные случаи уравнения неразрывности. В случае установившегося (стационарного) движения и из (2.16) следует

. (2.22)

В случае постоянства плотности среды из (2.21) следует

. (2.23)

Проинтегрировав уравнение (2.22), либо на основании (2.3) можно получить уравнение постоянства расхода, применимое для установившегося движения среды, полностью заполняющей поперечное сечение канала площадью S:

, (2.24)

где средняя по перечному сечению скорость среды.

Выше было рассмотрено движение среды в целом. Для многокомпонентных систем нетрудно получить закон сохранения массы в локальной форме для каждого компонента:

. (2.25)

В общем случае закон сохранения массы применительно к единичному объему можно сформулировать следующим образом:

.

При рассмотрении многофазных систем уравнения вида (2.25) могут записываться для каждой фазы в отдельности. Если при этом происходит перенос массы компонента из одной фазы в другую, то он может учитываться в источнике массы .

В разделе 1.3.1. уже говорилось, что для многокомпонентных сред обычно используют потоки не массы, а вещества, и вместо плотности компонентов их мольные концентрации. Поделив уравнение (2.25) на мольную массу компонента m_i, получим

. (2.26)

Рассмотрим наиболее простой случай массопереноса в двухкомпонентной среде при отсутствии химических реакций. Применяя выражение для потока компонента в среднемассовой системе отсчета, можно записать уравнение нестационарной конвективной диффузии:

. (2.27)

Используя допущение о постоянстве , учитывая, что при этомпо (2.23), получим

. (2.28)

В случае равенства нулю среднемассовой скорости в лабораторной системе отсчета , 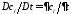и допустив , получим уравнение, называемоевторым законом Фика:

. (2.29)

Если предположить при этом стационарность процесса, то оно еще более упростится:

. (2.30)

Таким образом, на основе закона сохранения и уравнения переноса массы получены дифференциальные уравнения, решив которые можно определить поля концентраций и массовых потоков компонентов в любом аппарате. Интегрирование дифференциальных уравнений дает общее решение, справедливое для класса процессов. Для получения конкретного частного решения необходимо дополнить уравнение условиями однозначности. Подробнее этот вопрос будет обсуждаться в разделе 2.4.