9.4. Нестационарный теплообмен

В инженерной практике достаточно часто приходится иметь дело с процессом нестационарного теплообмена. Нестационарными являются все периодические процессы. Для непрерывных процессов выход на режим также является нестационарным процессом. Решение задач нестационарного теплообмена представляет значительную сложность с точки зрения математики.

Нестационарный кондуктивный теплообмен. Нестационарный теплообмен в отсутствие конвективного и турбулентного механизмов переноса имеет место в твердых телах и описывается уравнением нестационарной теплопроводности Фурье (2.47). Для получения решения, соответствующего конкретным условиям проведения процесса, необходимо дополнить уравнение Фурье условиями однозначности. Начальное условие должно содержать распределение температуры в твердом теле в начальный момент времени Т_т(0, х, y, z). Граничные условия должны отражать особенности теплообмена на поверхности тела (на стенках). Они могут быть различного рода:

1. В граничных условиях первого рода задается распределение температуры на поверхности тела для каждого момента времени:

. (9.163)

2. В граничных условиях второго рода известной величиной является тепловой поток на поверхности тела, что позволяет записать равенство, в котором производная от температуры взята по нормали к поверхности в каждой ее точке:

. (9.164)

3. Граничные условия третьего рода предусматривают задание условий теплообмена твердого тела с внешней средой в виде уравнения теплоотдачи, в котором известными считаются коэффициент теплоотдачи _ср(t, x_ср, y_ср, z_ср) и температура среды T_ср(t, x^я, y^я, z^я):

. (9.165)

4. Граничные условия четвертого рода записываются как равенство тепловых потоков в теле и окружающей среде на границе их соприкосновения с учётом того, что вблизи твердой непроницаемой поверхности единственным механизмом переноса в среде является молекулярный:

. (9.166)

Уравнение нестационарной теплопроводности (2.47) является линейным однородным дифференциальным уравнением второго порядка с частными производными. Оно имеет бесчисленное множество частных решений и относится к разряду уравнений математической физики, для решения которых разработаны специальные методы. Анализу этого уравнения в зависимости от вида условий однозначности посвящены целые тома, например, [40], где приводятся решения для наиболее распространенных случаев как в аналитическом виде, так и виде таблиц или номограмм.

Рассмотрим простейший случай нестационарного кондуктивного теплообмена нагревание (охлаждение) полубесконечного слоя твердого материала, занимающего пространство отy = 0 до y = . Предположим, что его температура равнялась Т₀, а затем в начальный момент времени на границе скачкообразно изменилась до значения Т_cт и поддерживается такой в дальнейшем. Требуется определить поле температуры в теле для каждого момента времени, т. е. найти Т(t, y) при t, y > 0. Задача является пространственно одномерной, и уравнение Фурье (2.47) примет вид

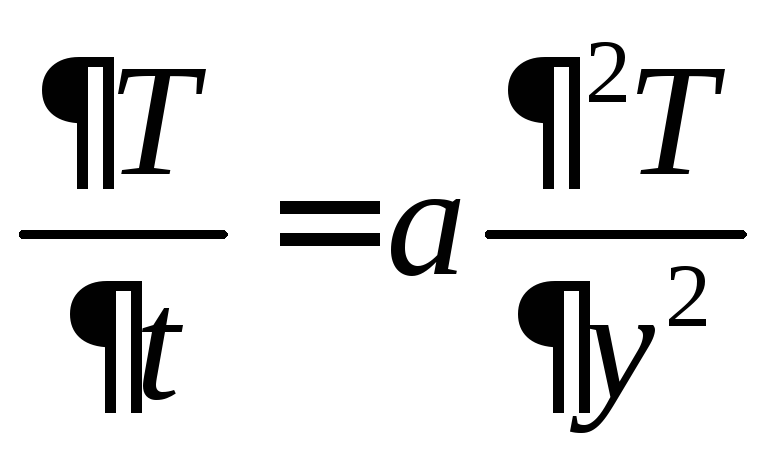. (9.167)

Запишем начальные и граничные условия:

. (9.168)

Допустим, что коэффициент температуропроводности будет постоянной величиной а = const. Температура является функцией двух независимых переменных t и y. Используя теорию подобия, перейдем к обобщенным переменным, сократив их число. Поделив левую часть уравнения (9.167) на правую, получим

. (9.169)

Для удобства введем переменную , а также безразмерную температуру(₁), которая будет являться уже функцией одной переменной ₁:

, (9.170),

. (9.171)

Чтобы записать уравнение (9.167) в новых переменных, найдем производные от сложных функций:

, (9.172)

, (9.173)

. (9.174)

Подставив найденные производные (9.172) и (9.174) в (9.167), получим обыкновенное дифференциальное уравнение второго порядка:

, (9.175)

(0) = 1, () = 0. (9.176)

Сделаем еще одну замену переменной, сведем (9.175) к уравнению первого порядка и решим, разделяя переменные:

, (9.177) , (9.178)

, (9.179) , (9.180)

, (9.181)

, (9.182)

. (9.183)

Введем еще одну переменную  = ₁/2 и определим константы интегрирования из граничных условий (9.176):

, (9.184)

. (9.185)

Определенный интеграл в правой части является табличным и равен , тогда

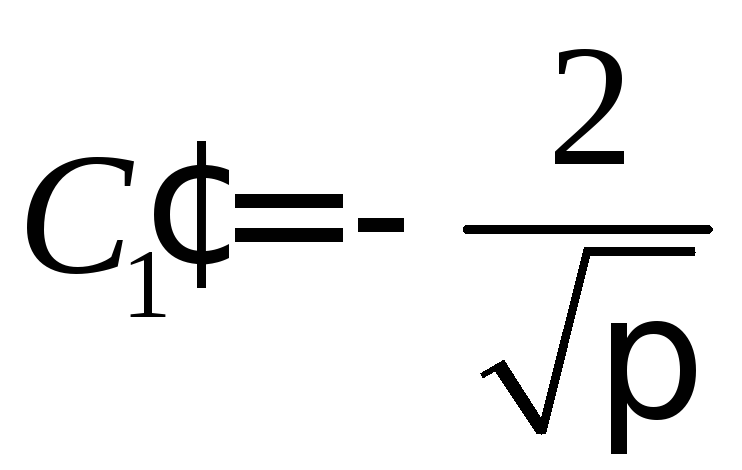, (9.186)

, (9.187)

где erf() табулированный в справочниках интеграл ошибок. Вид зависимости() представлен на рис. 9.16.

Рис. 9.16. Зависимость безразмерной температуры от безразмерной переменнойдля нестационарного теплообмена в полубесконечном слое твердого материала

Рассмотрим еще один типичный пример нестационарного кондуктивного теплообмена охлаждение бесконечной плоской пластины толщиной 2, помещенной в среду с постоянной температурой Т_cp (рис. 9.17). Задача, как и в рассмотренном выше случае, является пространственно одномерной и описывается уравнением (9.167).

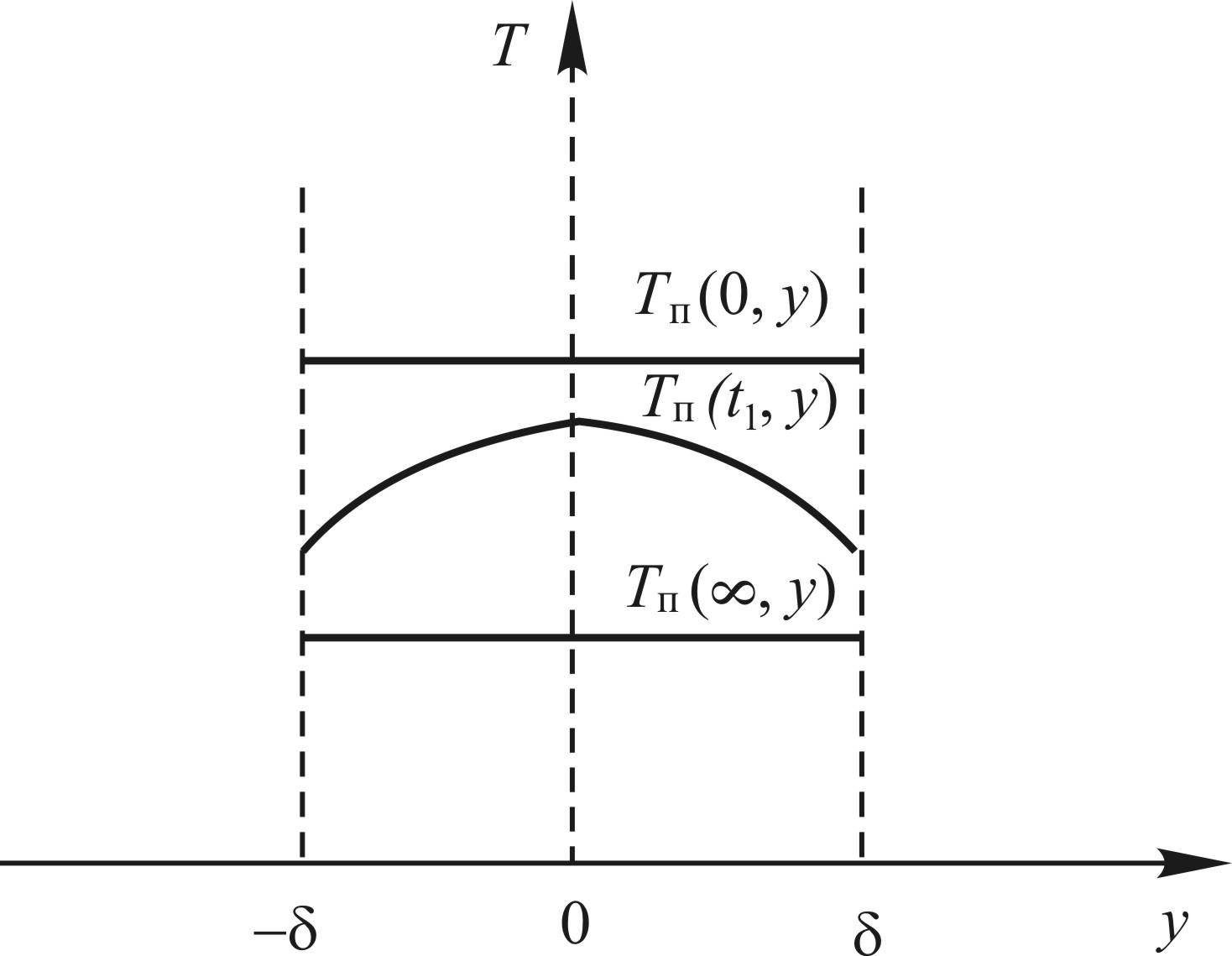
Рис. 9.17. Профили температуры при охлаждении пластины в различные моменты времени

Предположим, что в начальный момент времени температура пластины была однородной Т_п(0, y) = Т₀ = const. В качестве граничных условий для данного примера имеет смысл использовать граничные условия третьего рода (9.165):

. (9.188)

Допустим, что теплофизические свойства пластины неизменны _п, а_п, с_рп = const, a _ст = _п. Аналитическое решение даже для такого простого примера представляет собой сумму бесконечного ряда. Используя теорию подобия, можно получить определяющие критерии и безразмерные переменные, с помощью которых удобно записать решение. Преобразованием уравнения (9.167) найдем известный нам критерий Фурье (4.54), а из (9.188) критерий Био (Bi):

, (9.189) 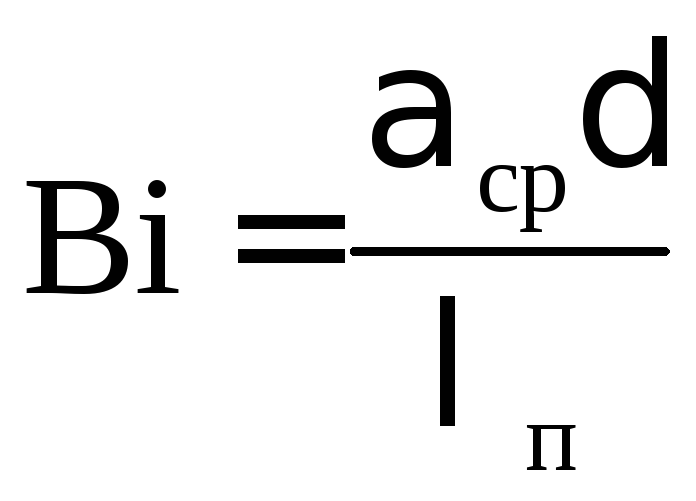. (9.190)

По своей записи критерий Bi сходен с критерием Нуссельта (4.61). Однако смысл его совершенно иной. Если при определении Nu все величины характеризуют одну фазу, то в критерии Bi коэффициент теплоотдачи характеризует теплообмен во внешней среде, а _п и  внутри тела. Если Bi >> 1, то термическое сопротивление сосредотачивается внутри твердого тела (внутренняя задача), а граничные условия 3-го рода переходят в условия 1-го рода, так какТ_ст  T_ср. Если же Bi << 1, то сопротивление теплообмена сосредотачивается во внешней среде (внешняя задача) и Т_п(t, y)  T_п(t, ). Вводя безразмерную температуру , решение можно представить в виде критериального уравнения, которое позволит определить температуру пластины Т(t, y) в любой момент времени t на любом расстоянии y:

. (9.191)

Обычно пользуются не аналитическими (слишком сложными), а графическими зависимостями, представленными в виде номограмм. Характер изменения поля температуры в пластине со временем показан на рис. 9.18 для различных значений критерия Биo.

Рис. 9.18. Профили безразмерной температуры  при охлаждении пластины для различных значений критериев Фурье и Био: а) Bi; б) Bi; в) – 0<Bi<

В зависимости от сложности условий однозначности (форма тела, его теплофизические свойства, вид граничных условий и т.д.) соотношения типа (9.187) могут быть получены аналитическим или численным решением уравнения Фурье либо с помощью метода физического моделирования, а также с использованием аналогово-изоморфных моделей, например, электрических, но описывающихся такими же дифференциальными уравнениями.

Нестационарный конвективный теплообмен. Описание нестационарного конвективного теплообмена представляет еще большую сложность, так как требует решения уравнения нестационарной конвективной теплопроводности (2.45) совместно с уравнением движения (2.55). Изменение поля температур во времени в общем случае будет описываться соотношениями вида (4.58), содержащими в отличие от (9.191) дополнительно определяющие критерии Рейнольдса, Прантдля, Фруда (или его модификации: Ga, Ar, Gr).

Рассмотрим простейший случай нестационарного конвективного теплообмена нагрев насыщенным паром жидкости объемомV в аппарате с мешалкой. При интенсивном перемешивании можно допустить структуру потока, соответствующую модели идеального смешения, что позволит считать температуру жидкости одинаковой во всех точках аппарата и применить закон сохранения энергии в интегральной форме (2.41) вместо (2.45). Изменения энтальпии системы за единицу времени равно количеству подводимого за это время тепла. Допустим неизменность теплофизических свойств жидкости и, следовательно, коэффициента теплопередачи (K_т = const).

или . (9.192)

Разделим переменные и проинтегрируем по времени, обозначив температуру жидкости в начальный момент времени Т₀. Учитываем, что температура конденсации пара постоянна Т_п = const.

, (9.193) , (9.194)

. (9.195)

По уравнению (9.194) можно определить температуру нагреваемой жидкости Т в любой момент времени t, а по (9.195) решить обратную задачу - найти время, необходимое для нагревания жидкости от температуры Т₀ до Т.