9.2.3. Физическое моделирование конвективного теплообмена

В предыдущих разделах рассмотрение конвективного теплообмена базировалось на решении дифференциальных уравнений, составляющих исчерпывающее описание переноса импульса и тепла. При этом исчерпывающее описание по возможности упрощалось: трехмерная постановка задачи сводилась к двухмерной, рассматривались простейшие граничные условия, теплофизические характеристики теплоносителя считались неизменными, теплоноситель представлял собой одну сплошную фазу. Все эти упрощения позволили получить явный вид решения, содержащего поля скоростей и температуры, потоков импульса и тепла, а также коэффициенты импульсо- и теплоотдачи.

Однако не для всех практически важных случаев такие упрощения, а следовательно, и теоретические решения возможны. Тогда пользуются методом физического моделирования. При этом, как правило, определяются лишь коэффициенты теплоотдачи, необходимые для инженерных расчетов. Определяемым критерием является критерий Нуссельта, а определяющие критерии и симплексы подобия выявляются из анализа дифференциальных уравнений. Вид критериальной зависимости находится путем обработки опытных данных. Надежное использование критериальных уравнений возможно лишь в изученной области изменения определяющих критериев подобия. Рассмотрим несколько наиболее характерных случаев, требующих использования физического моделирования.

Теплообмен с телами сложной формы. Ранее в данной главе были получены решения для теплообмена потока, движущегося параллельно твердой поверхности (плоская пластина, труба). Ситуация усложняется при омывании криволинейной поверхности. Рассмотрим, например, часто встречающееся поперечное обтекание цилиндра ламинарным потоком (рис. 9.10). На лобовой части поверхности образуется ламинарный пограничный слой, толщина которого возрастает по мере увеличения угла .

Рис. 9.10. Поперечное обтекание цилиндра ламинарным потоком

При обтекании лобовой части ( < 90) сечение потока сужается, скорость возрастает, давление падает. В кормовой части ( > 90) наблюдается обратная картина. Возрастание давления в кормовой части, а также и силы инерции приводят к тому, что, начиная с некоторой точки В, слои жидкости в пограничном слое начинают двигаться в обратном направлении. Происходит так называемый «отрыв» пограничного слоя, он оттесняется обратным потоком от поверхности. В части цилиндра за точкой отрыва уравнения пограничного слоя не применимы, что не позволяет получить аналитического решения для данного случая.

Экспериментальные исследования свидетельствуют об уменьшении локального коэффициента теплоотдачи по мере увеличения угла  до точки В, а затем о его увеличении (рис. 9.11). Это понятно, так как коэффициент теплоотдачи обратно пропорционален толщине пограничного слоя. В точке отрыва В пограничный слой разрушается, образуются вихри, способствующие интенсификации теплообмена. В справочной литературе обычно приводятся критериальные уравнения для осредненного по всей поверхности цилиндра коэффициента теплоотдачи . Качественный вид зависимости критерия Нуссельта при этом совпадает с (9.51), полученным для плоской пластины. Отличие заключается в несколько иных значениях числовых коэффициентов, а также в выборе в качестве характерного линейного размера наружного диаметра цилиндраd. Однако гидродинамическая аналогия при этом отсутствует, так как наличие градиента давления нарушает идентичность уравнений движения и конвективной теплопроводности. Явление "отрыва" наблюдается в области ламинарного обтекания цилиндра при Re_d > 5. В случае, если угол между скоростью набегающего потока и осью цилиндра  (угол атаки) отличается от 90, то в уравнение вводится поправочный коэффициент (), значения которого приведены в таблицах.

Рис. 9.11. Зависимость отношения локального коэффициента теплоотдачи к среднему от угла  для цилиндра при поперечном обтекании

При турбулизации пограничного слоя (Re_d = 210⁵) можно отметить, что точка отрыва достигается при больших значениях угла _В, а также появляется второй максимум на кривой , соответствующий переходу от ламинарного пограничного слоя к турбулентному.

Другим примером, требующим физического моделирования по причине сложной формы поверхности, может служить теплообмен с шероховатой поверхностью. Под шероховатостью понимаются неровности, бугорки, характерный линейный размер которых значительно меньше характерного линейного размера рассматриваемой задачи (диаметра трубы, цилиндра, толщины пограничного слоя и т.д.). Наличие шероховатости практически не сказывается на теплообмене при ламинарном режиме течения, а также при турбулентном, если высота бугорков меньше толщины вязкого подслоя. Если же высота бугорков больше толщины вязкого подслоя, то коэффициент теплоотдачи может изменяться в несколько раз, как правило, увеличиваясь.

Обтекание потоком каждого бугорка можно рассматривать по аналогии с обтеканием криволинейной поверхности, например, цилиндра. При этом отрыв пограничного слоя и завихрения потока, т.е. возмущения, которые могут образовываться в области ламинарного течения, быстро затухают, чему способствуют близость стенки и малая скорость потока вблизи нее. Возмущения, образующиеся в турбулентной области, приводят к увеличению коэффициентов турбулентного обмена, что соответствующим образом сказывается на коэффициенте теплоотдачи. При этом величина коэффициента теплоотдачи зависит от высоты и формы бугорков, а также от расстояния между ними. Результаты физического моделирования, учитывающие эти зависимости, приведены в литературе [35–39]. Создание искусственной шероховатости может применяться для интенсификации теплообмена, однако при этом необходимо помнить об увеличении гидравлического сопротивления аппарата.

Влияние на теплообмен изменения теплофизических характеристик теплоносителя. Во всех ранее рассмотренных примерах мы допускали неизменность теплофизических характеристик потока ,  с_p,  = const. Однако в условиях теплообмена при наличии неоднородности температуры такое допущение не всегда оправдано, так как все эти величины в большей или меньшей степени зависят от температуры. Влияние изменения теплофизических характеристик теплоносителя на теплообмен может осуществляться за счет двух факторов. Первый заключается в невозможности вынесения за операторы дифференцирования в уравнениях движения и энергии (2.55), (2.45) вышеуказанных величин и необходимости совместного решения этих уравнений с учетом зависимости теплофизических характеристик от температуры. Второй фактор состоит в возникновении под действием силы тяжести при неоднородной плотности явления естественной конвекции, для учета которого видоизменяют правую часть уравнения движения. Совместное влияние этих факторов не позволяет получить аналитического решения уравнений, составляющих исчерпывающее описание процессов переноса, и для нахождения коэффициентов теплоотдачи используется метод физического моделирования.

Рассмотрим вначале влияние на теплообмен первого фактора. Как показывают экспериментальные исследования, это влияние имеет смысл учитывать лишь для жидких теплоносителей, в газовой фазе при умеренных скоростях потока оно не существенно. Наиболее значительное влияние на теплообмен оказывает изменение вязкости жидкости. Проанализируем это влияние на простейшем примере ламинарного пограничного слоя на плоской пластине. Допустим, что идет процесс охлаждения теплоносителя, тогда >Т_ст, ^я < ^ст, так как   ~ T^-1. Вязкость в пограничном слое будет увеличиваться по сравнению с вязкостью в ядре потока. Это в соответствии с (9.27) и (9.31) приведет к увеличению толщины гидродинамического и теплового пограничных слоев, а по (9.47) – к уменьшению коэффициента теплоотдачи ( ~ _т^-1 ~ ^-0,17). И наоборот, при нагревании теплоносителя вязкость в пограничном слое меньше, чем в ядре потока, толщина слоя меньше, а коэффициент теплоотдачи больше, чем при постоянном значении коэффициента вязкости, соответствующем температуре в ядре потока. Теоретически учесть количественно влияние изменения вязкости достаточно сложно, так как при этом будут меняться профили скоростей и температуры в пограничном слое, нарушится гидродинамическая аналогия.

Экспериментальные исследования показали возможность учета этого фактора за счет введения множителей _t для расчета  или Nu:

или (9.133)

Индекс «ж» указывает на необходимость использования теплофизических характеристик теплоносителя при температуре ядра потока, а индекс «ст» при температуре стенки. Причем эти множители пригодны не только для ламинарного, но и турбулентного пограничного слоя и не только на плоской пластине, но и при обтекании цилиндра, вынужденного течения в трубе и ряда других случаев. При использовании критериальных уравнений следует обращать особое внимание на характерные величины, применяемые для нахождения критериев. Одной из таких величин является определяющая температура, при которой должны определяться соответствующие величины. В качестве определяющей температуры может быть выбрана среднемассовая температура в сечении трубы, температура стенки, средняя величина между температурами стенки и ядра потока и т.д. Использование иной, отличной от предусмотренной авторами обобщений определяющей температуры, может привести к существенным погрешностям расчета.

Рассмотрим влияние на теплообмен второго фактора, обусловленного явлением естественной конвекции, которое возникает за счет действия подъемной силы. Подъемная сила является результирующей сил гидростатического давления и тяжести. В условиях постоянной плотности среды эти силы уравновешивают друг друга и = 0 (5.1). В случае неоднородной плотности сила тяжести, действующая на элементарный объем среды с большей плотностью, превышает силу гидростатического давления, подъемная сила совпадает по направлению с силой тяжести и элементарный объем движется вниз. И наоборот, элементарный объем среды с плотностью меньше средней в данном горизонтальном сечении движется вверх, так как результирующая подъемная сила совпадает по направлению с силой гидростатического давления.

По аналогии с пограничным слоем на плоской горизонтальной пластине при вынужденном движении потока рассмотрим пограничный слой на полубесконечной вертикальной пластине при естественной конвекции. Ось х расположим в вертикальном направлении, начиная с кромки пластины, совпадающей с плоскостью хz. Пластина, имеющая температуру T_ст, окружена большим объемом среды с температурой . Все теплофизические характеристики среды, за исключением плотности, будем считать постоянными. ПриТ_ст = среда будет находиться в покое. ЕслиТ_ст > , то вблизи пластины плотность будет меньше и образуется поднимающийся вверх тонкий пограничный слой (рис. 9.12).

По аналогии с пограничным слоем на горизонтальной пластине при вынужденной конвекции можно получить уравнения гидродинамического и теплового пограничных слоев для рассматриваемого случая. Отличие будет заключаться в правой части уравнения движения (9.21), в которую необходимо добавить слагаемое g_x(T ), обусловленное подъемной силой:

, (9.134) , (9.135)

, (9.136)

при Т = = const,, (9.137)

где  коэффициент объемного расширения.

Поскольку в условиях рассматриваемой задачи площадь поперечного сечения пограничного слоя с плотностью  бесконечно мала по сравнению с площадью сечения среды с плотностью ⁰, то среднюю плотность можно принять равной ⁰ и использовать (9.137) для нахождения градиента гидростатического давления в условиях конвекции

. (9.138)

Рис. 9.12. Гидродинамический и тепловой пограничные слои на вертикальной плоской пластине при естественной конвекции

Некоторые отличия будут и в граничных условиях по сравнению с (9.23), так как скорость на внешней границе пограничного слоя будет равна нулю. Решение данной системы дифференциальных уравнений было получено Польгаузеном. Наличие подъемной силы в уравнении движения и видоизменение граничных условий приводят к нарушению гидродинамической аналогии теплоотдачи, изменения температуры и скорости в пограничном слое имеют принципиально различный характер (рис. 9.12). Так как условия однозначности не содержат характерной скорости, а в уравнении движения присутствует сила тяжести, то в качестве определяющего критерия для нахождения коэффициента теплоотдачи используется модифицированный критерий Фруда, а именно, критерий Грасгофа (4.70).

В нем характерной линейной величиной является расстояние от кромки пластины х, а Т = Т_ст:

. (9.139)

Следует отметить, что в данном случае коэффициент теплоотдачи будет зависеть от величины движущей силы Т_ст . Для учета изменения остальных теплофизических свойств в пограничном слое могут быть использованы множители_t (9.133).

При Gr_xPr > 10⁹ пограничный слой становится турбулентным, для него применимо соотношение

. (9.140)

Аналогичный вид имеют критериальные соотношения для определения коэффициентов теплоотдачи от тел иной формы при естественной конвекции в неограниченном объеме теплоносителя.

Рис. 9.13. Циркуляционные токи при естественной конвекции в ограниченном сосуде: а – вертикальный сосуд с Т_ст> ; б – вертикальная щель с Т_ст,2> Т_ст,1; в – горизонтальная труба с Т_ст< .

В случае естественной конвекции в ограниченном объеме возникают, как правило, циркуляционные токи теплоносителя (рис. 9.13). Зачастую свободная и вынужденная конвекции наблюдаются одновременно, например, при течении в трубе (рис. 9.13в). В этом случае определяющими критериями служат Re, Gr, Pr. Показатели степени в множителе _t могут отличаться от (9.133) и иметь различные значения для нагревания и охлаждения теплоносителя.

Теплообмен при изменении фазового состояния теплоносителя. Наиболее часто встречающиеся случаи теплообмена с изменением фазового состояния конденсация и кипение. Они характеризуются высокими коэффициентами теплоотдачи, что обусловливает их применение в теплообменных аппаратах. Рассмотрим вначале первый из них. Конденсация пара на твердой поверхности происходит при условии, что температура стенки меньше температуры насыщения пара Т_ст < . Возможны два варианта конденсации: пленочная и капельная. Если твердая поверхность смачивается конденсатом, то происходит пленочная конденсация, а если не смачивается - капельная.

Рассмотрим простейший случай пленочной конденсации чистого насыщенного неподвижного пара на плоской вертикальной поверхности x – z. Начало координат совместим с точкой начала процесса конденсации. По мере стекания пленки вниз толщина ее будет увеличиваться вследствие увеличения количества сконденсировав­шегося пара. В процессе теплоотдачи от пара к стенке можно выделить три стадии, каждая из которых обладает собственным термическим сопротивлением: 1) подвод тепла и вещества от пара к пленке, 2) собственно конденсация, 3) перенос тепла через пленку жидкого конденсата. Первая стадия осуществляется за счет конвективного механизма переноса, обусловленного градиентом давления, возникающим при переходе пара в жидкость. Эффективность конвективного механизма гораздо выше молекулярного, за счет которого переносится тепло через пленку, что позволяет пренебречь сопротивлением первой стадии. Сопротивление второй стадии при достаточно высоких давлениях (для водяного пара при р > 10⁴ Па) также невелико. Это позволяет допустить, что все сопротивление теплоотдачи и соответственно все изменение температуры сосредоточено в пленке конденсата. Необходимо отметить, что температура насыщенного пара при теплообмене не меняется (при р = const) и все тепло, отдаваемое им, обусловлено изменением энтальпии фазового перехода = const. Определим коэффициент теплоотдачи:

. (9.141)

При условии Т_ст, = const можно допустить, что для стационарного теплообмена, т.е.= const или= 1. Это позволяет достаточно просто найти коэффициент теплоотдачи по (4.9). Допустим, что теплофизические характеристики пленки неизменны.

В верхней части пластины (х, , Re_ – невелики) наблюдается ламинарный безволновой режим течения пленки Re_ < 3 (см. раздел 5.4). Для него

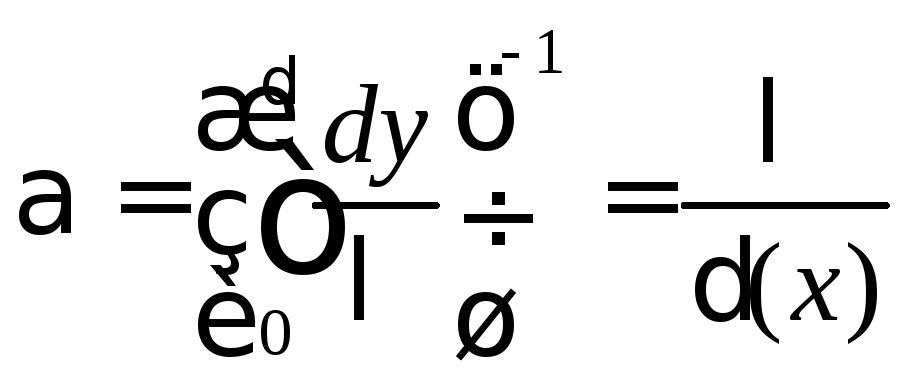, (9.142) . (9.143)

Как видно, гидродинамическая аналогия теплоотдачи в данном случае отсутствует (Nu_г, = 2), что объясняется различиями граничных условий, а также уравнений движения и энергии за счет присутствия в первом силы тяжести.

Для отыскания явного вида решения нужно определить (х). Учитывая, что изменение линейной плотности орошения Г пропорционально количеству сконденсировавшегося пара и соответственно потоку тепла, отнесенному к удельной теплоте конденсации, можно записать

. (9.144)

Подставив в (9.144)  из (5.131) и проинтегрировав от 0 до х, найдем Г(х):

. (9.145)

Подставив (9.145) в (5.131), определим (х), а затем по (9.143) локальный коэффициент теплоотдачи:

, (9.146)

. (9.147)

Средний по высоте коэффициент теплоотдачи будет равен

. (9.148)

Как видно из (9.147), локальный коэффициент теплоотдачи уменьшается по мере стекания пленки. Он, как и при естественной конвекции, зависит от движущей силы (–Т_ст), однако в данном случае эта зависимость обратная. Тем не менее поток тепла прямо пропорционален движущей силе, хотя зависимость эта уже нелинейная ~ (–Т_ст)^3/4. Учет изменения теплофизических характеристик в пленке может осуществляться с помощью поправочного множителя _t (9.133), в котором индекс «ж» заменить на «н».

По мере стекания конденсатной пленки и увеличения ее толщины (х) режим движения переходит в волновой, а затем и в турбулентный. Имея в виду = 1 достаточно легко определить коэффициент теплоотдачи и турбулентного режима течения по (4.9) при известных зависимостяхa_т(y) = _т(y).

Воспользовавшись соотношениями для _т в вязком подслое (9.77), вне его (9.56), а для 0,7  y   корреляцией Шлингера

, (9.149)

получим

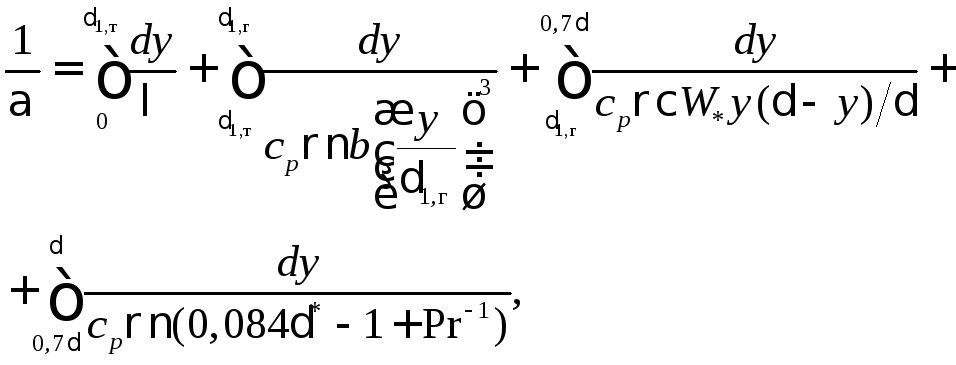(9.150)

(9.151)

где анаходится из (5.148).

Наличие гидродинамической аналогии теплоотдачи не наблюдается и при турбулентном течении пленки, так как (y)  (y).

Для получения явного вида  необходимо определить (х), для чего можно было бы проделать процедуру, аналогичную (9.144)(9.147). Однако на практике обычно используют более простые эмпирические корреляции, как и для волнового режима. Следует отметить высокие значения коэффициентов теплоотдачи при пленочной конденсации, что объясняется малой толщиной стекающей пленки, в которой сосредоточено все сопротивление. При капельной конденсации коэффициенты теплоотдачи еще больше, так как часть поверхности свободна от пленки.

При наличии в паре даже небольшого количества неконденси­рующихся газов коэффициент теплоотдачи резко уменьшается. Это объясняется образованием слоя газа вблизи поверхности пленки, через который перенос молекул пара осуществляется уже за счет молекулярного механизма, что приводит к возрастанию сопротивления первой стадии теплоотдачи.

Перейдем к рассмотрению теплообмена при кипении теплоносителя. Для осуществления процесса кипения необходимо, чтобы температура жидкости стала несколько выше температуры насыщения пара, т.е. жидкость должна быть перегретой. Добиться этого можно двумя способами: увеличить температуру жидкости или уменьшить температуру насыщения пара. Реализация второго способа связана с резким понижением давления в системе, что будет сопровождаться образованием пузырьков пара непосредственно в объеме жидкости. Однако на практике гораздо чаще применяется первый способ, тепло при этом подводится, как правило, через твердую поверхность. В этом случае образование пузырьков пара происходит на стенке, обладающей наибольшей температурой в системе. Рассмотрим этот процесс более подробно.

Наиболее благоприятные условия для образования пузырьков пара создаются в микровпадинах твердой поверхности, где достигается наибольший перегрев жидкости. Они являются центрами парообразования. Образовавшийся пузырек растет за счет испарения жидкости, достигая определенного размера, отрывается от твердой поверхности и под действием подъемной силы движется вверх. По мере всплытия происходит дальнейшее увеличение пузыря, так как продолжается испарение из перегретой жидкости. Температура кипящей жидкости при неизменных условиях (давление, состав) остается постоянной (перегрев, как правило, бывает незначительным), что позволяет считать все подводимое тепло идущим на изменение энтальпии фазового перехода, равной теплоте парообразования.

Кинетика процесса теплоотдачи при кипении существенно зависит от движущей силы процесса, равной разности температур стенки и кипящей жидкости Т_ст Т_к. При малых Т_ст Т_к перегрев жидкости недостаточен (область АВ на рис.9.14), и коэффициент теплоотдачи может определяться по

Рис. 9.14. Тепловой поток , Вт/м² и коэффициент теплоотдачи , Вт/м²К, при кипении воды

соотношениям, полученным для естественной конвекции без учета кипения. При дальнейшем увеличении движущей силы происходит интенсификация образования, отрыва и всплытия пузырей, что ведет к перемешиванию жидкости вблизи стенки, ее турбулизации, уменьшению толщины пограничного слоя и, следовательно, к резкому увеличению коэффициента теплоотдачи (область ВС). По достижении критической точки С область пузырькового кипения сменяется областью пленочного кипения. При этом отдельные пузырьки сливаются вблизи твердой поверхности в сплошную пленку пара, а учитывая, что коэффициенты теплопроводности в паровой фазе значительно ниже, чем в жидкой, это приводит к резкому уменьшению коэффициента теплоотдачи. Таким образом, проектирование эффективных теплообменных аппаратов требует выбора оптимальной движущей силы теплоотдачи. В связи со сложностью процесса теплообмена при кипении для его описания обычно используется метод физического моделирования.

Разумеется, мы рассмотрели не все возможные случаи конвективного теплообмена. В данном разделе мы попытались показать основные закономерности и подходы к решению наиболее часто встречающихся задач. Описание других примеров конвективного теплообмена, например, в аппаратах с механическим перемешиванием или непосредственным контактом газового и жидкого теплоносителей, а также критериальные уравнения для коэффициентов теплоотдачи можно найти в специальной литературе.