
- •Глава 9. Теплообмен
- •9.1. Кондуктивный теплообмен
- •9.2. Конвективный теплообмен
- •9.2.1. Гидродинамический и тепловой пограничные слои на плоской пластине
- •9.2.2. Теплообмен в трубах
- •9.2.3. Физическое моделирование конвективного теплообмена
- •9.3. Теплообмен излучением
- •9.4. Нестационарный теплообмен
- •9.5. Оптимизация теплообмена
- •Для турбулентного режима
- •Контрольные вопросы к главе 9
- •Вопросы для обсуждения
9.2.2. Теплообмен в трубах
Рассмотрим стационарный теплообмен между стенками горизонтальной прямой трубы круглого сечения и потоком, обладающим неизменными теплофизическими характеристиками и движущимся за счет вынужденной конвекции внутри нее.
Участки
гидродинамической и термической
стабилизации.
При движении
потока в трубе на начальном участке
длиной
![]() существует
гидродинамический пограничный слой,
расширяющийся по мере удаления от входа
до тех пор, пока не заполнит все сечение
(участок гидродинамической стабилизации).
Далее выделение ядра потока и пограничного
слоя не имеет смысла, так как скорость
Wx
меняется по
всему поперечному сечению трубы, при
этом профиль скорости уже не зависит
от продольной координаты - такое течение
называется стабилизированным (рис. 9.6
а).
существует
гидродинамический пограничный слой,
расширяющийся по мере удаления от входа
до тех пор, пока не заполнит все сечение
(участок гидродинамической стабилизации).
Далее выделение ядра потока и пограничного
слоя не имеет смысла, так как скорость
Wx
меняется по
всему поперечному сечению трубы, при
этом профиль скорости уже не зависит
от продольной координаты - такое течение
называется стабилизированным (рис. 9.6
а).

а) ![]()

б) ![]()
Рис. 9.6. Профили безразмерных скорости а) и температуры б) на начальных и стабилизированных участках при ламинарном течении в цилиндрической трубе
Аналогичным
образом в трубе при наличии теплообмена
можно выделить участок термической или
тепловой стабилизации
![]() начальный участок длиной
начальный участок длиной
![]() ,
на котором существует тепловой пограничный
слой. Прих >
,
на котором существует тепловой пограничный
слой. Прих > ![]() (область стабилизированного теплообмена)
характер радиального изменения
температуры не зависит от продольной
координаты, однако величина средней по
сечению температуры стремится к
температуре стенки прих
в отличие от средней скорости, не
меняющейся для трубы постоянного сечения
рис. 9.6 б.
(область стабилизированного теплообмена)
характер радиального изменения
температуры не зависит от продольной
координаты, однако величина средней по
сечению температуры стремится к
температуре стенки прих
в отличие от средней скорости, не
меняющейся для трубы постоянного сечения
рис. 9.6 б.
Характеристики
пограничных слоев в трубе и на плоской
пластине несколько отличаются. Это
обусловлено различием формы обтекаемых
поверхностей, переменностью скорости
ядра потока в трубе
![]() (х)
и наличием градиента давления p/x 0.
Увеличение скорости ядра потока на
участке гидродинамической стабилизации
следует из уравнения постоянства расхода
(2.24), в соответствии с которым средняя
скорость в канале неизменного сечения
для установившегося течения несжимаемой
жидкости должна быть постоянной.
Поскольку в пограничном слое скорость
уменьшается от
(х)
и наличием градиента давления p/x 0.
Увеличение скорости ядра потока на
участке гидродинамической стабилизации
следует из уравнения постоянства расхода
(2.24), в соответствии с которым средняя
скорость в канале неизменного сечения
для установившегося течения несжимаемой
жидкости должна быть постоянной.
Поскольку в пограничном слое скорость
уменьшается от
![]() до 0, то по мере увеличения его толщины
до 0, то по мере увеличения его толщины![]() должна возрастать. Падение давления в
трубеp/x
< 0 следует из уравнения Бернулли (2.38)
применительно к ядру потока. Несмотря
на эти отличия, наблюдается качественное
сходство пограничных слоев в трубе и
на пластине.
должна возрастать. Падение давления в
трубеp/x
< 0 следует из уравнения Бернулли (2.38)
применительно к ядру потока. Несмотря
на эти отличия, наблюдается качественное
сходство пограничных слоев в трубе и
на пластине.
Рассмотрим ламинарное движение потока. При Pr > 1 тепловой пограничный слой будет находиться внутри гидродинамического, следовательно, длина участка термической стабилизации (расстояние от входа, на котором т = R) будет больше, чем гидродинамической (г = R). Решение соответствующих уравнений для пограничных слоев в трубе с постоянной температурой стенки дает зависимость
![]() ,
(9.89)
,
(9.89)
![]() .
(9.90)
.
(9.90)
Так,
для чисел
Re = 2103
это составит
![]() 100 d,
т.е. при ламинарном движении длина
участка гидродинамической стабилизации
может достигать 100 диаметров, а термической
и того больше. Это приводит к тому, что
в большинстве случаев, особенно для
жидкостей с большим значением критерия
Прандтля, теплообмен при ламинарном
режиме движения осуществляется в
основном на участке термической
стабилизации. Как и для пограничного
слоя на плоской пластине, коэффициент
теплоотдачи для трубы на участке
термической стабилизации уменьшается
по мере удаления от входа (увеличивается
толщина пограничного слоя), увеличиваясь
пропорционально скорости потока и
коэффициенту теплопроводности
теплоносителя. В качестве характерных
для труб величин принято использовать:
диаметр d,
среднюю скорость
100 d,
т.е. при ламинарном движении длина
участка гидродинамической стабилизации
может достигать 100 диаметров, а термической
и того больше. Это приводит к тому, что
в большинстве случаев, особенно для
жидкостей с большим значением критерия
Прандтля, теплообмен при ламинарном
режиме движения осуществляется в
основном на участке термической
стабилизации. Как и для пограничного
слоя на плоской пластине, коэффициент
теплоотдачи для трубы на участке
термической стабилизации уменьшается
по мере удаления от входа (увеличивается
толщина пограничного слоя), увеличиваясь
пропорционально скорости потока и
коэффициенту теплопроводности
теплоносителя. В качестве характерных
для труб величин принято использовать:
диаметр d,
среднюю скорость
![]() ,
среднюю температуру
,
среднюю температуру![]() :
:
 ,
(9.91)
,
(9.91)
![]() ,
(9.92)
,
(9.92)
 (9.93)
(9.93)
Значение
коэффициента В
зависит от вида граничных условий на
стенке трубы, так, для Тст = const
B = 1,03.
В соответствии с (4.18) можно найти
осредненный по длине трубы
х
коэффициент теплоотдачи
![]() (x).
Выражение для него будет аналогичным
(9.93), но в 1,5 раза больше, т.е. коэффициент
В
будет равен 1,55.
(x).
Выражение для него будет аналогичным
(9.93), но в 1,5 раза больше, т.е. коэффициент
В
будет равен 1,55.
Наглядное
представление температуры
![]() ,
определяемой (9.91) и называемой
среднемассовой, можно составить, если
найти температуру всей массы потока,
вышедшей из данного сечения трубы за
достаточно короткий промежуток времени
(это существенно лишь для нестационарных
процессов) и затем полностью перемешанной.
Использование такой температуры
позволяет представить теплообмен в
трубе пренебрегая молекулярным и
турбулентным переносом в продольном
направлении по сравнению с конвективным,
происходящим в режиме идеального
вытеснения, т.е. полагать, что количество
тепла, переносимое в направлении осих
за единицу
времени через сечение трубы, пропорционально
средней конвективной скорости
,
определяемой (9.91) и называемой
среднемассовой, можно составить, если
найти температуру всей массы потока,
вышедшей из данного сечения трубы за
достаточно короткий промежуток времени
(это существенно лишь для нестационарных
процессов) и затем полностью перемешанной.
Использование такой температуры
позволяет представить теплообмен в
трубе пренебрегая молекулярным и
турбулентным переносом в продольном
направлении по сравнению с конвективным,
происходящим в режиме идеального
вытеснения, т.е. полагать, что количество
тепла, переносимое в направлении осих
за единицу
времени через сечение трубы, пропорционально
средней конвективной скорости
![]() и температуре
и температуре![]() при условии
cp,
= const:
при условии
cp,
= const:
 .
(9.94)
.
(9.94)
Использование
модели идеального вытеснения при условии
Тст = const
вне зависимости от характера изменения
(x)
позволяет считать, как это было показано
в разделе 4.1, среднюю движущую силу
среднелогарифмической величиной (4.31).
Таким образом, (9.93) для
![]() (x)
и (4.31) для
(x)
и (4.31) для
![]() дают возможность применять уравнение
теплоотдачи в интегральной форме, имея
явный вид выражений для всех величин.
дают возможность применять уравнение
теплоотдачи в интегральной форме, имея
явный вид выражений для всех величин.
Соотношение (9.93) получено для участка термической стабилизации, которому предшествовал участок гидродинамической стабилизации, т.е. теплообмен начался не со входа в трубу и при х = 0 течение было уже стабилизированным. В том случае, если теплообмен начинается непосредственно с кромки трубы и при х = 0 начинаются оба участка тепловой и гидродинамической стабилизации, то в непосредственной близости от входа в трубу при г << d локальный и средний коэффициенты теплоотдачи могут определяться по соотношениям (9.47), (9.50), найденным для плоской пластины. По мере увеличения толщины гидродинамического пограничного слоя начинают сказываться отличия, присущие движению в трубе. Для расчета среднего коэффициента теплоотдачи в этом случае удобнее воспользоваться соотношением (9.93) с поправочным множителем , учитывающим увеличение коэффициента теплоотдачи на участке гидродинамической стабилизации
 . (9.95)
. (9.95)
Если
необходимо определить средний коэффициент
теплоотдачи для трубы длиной
![]() ,
содержащей участки термической
стабилизации и стабилизированного
теплообмена, то осреднение можно
провести, учитывая, что в области
стабилизированного теплообмена при
ламинарном режиме величина
,
содержащей участки термической
стабилизации и стабилизированного
теплообмена, то осреднение можно
провести, учитывая, что в области
стабилизированного теплообмена при
ламинарном режиме величина
![]() не зависит отх,
обозначим ее
не зависит отх,
обозначим ее
![]() :
:
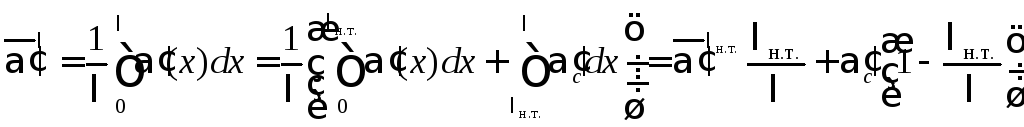 .
(9.96)
.
(9.96)
При турбулентном течении потока в трубе, как и на плоской пластине, толщины теплового и гидродинамического пограничных слоев, во-первых, совпадают, а во-вторых, растут значительно быстрее, чем для ламинарных. Это приводит к уменьшению длины участков термической и гидродинамической стабилизации, что позволяет в большинстве случаев пренебрегать ими при расчете теплоотдачи:
![]() .
(9.97)
.
(9.97)
Стабилизированный теплообмен при ламинарном движении. Уравнение (2.44) для стационарного теплообмена при стабилизированном течении в трубе удобнее записать в цилиндрических координатах (см. прил. 2.3):
![]() .
(9.98)
.
(9.98)
Как
правило, конвективный перенос тепла в
осевом направлении значительно выше
молекулярного
![]() ,
что позволяет пренебречь последним при
Ре > 100. С учетом этого допущения (9.98)
можно переписать
,
что позволяет пренебречь последним при
Ре > 100. С учетом этого допущения (9.98)
можно переписать
![]() .
(9.99)
.
(9.99)
Дополним это уравнение граничными условиями:
![]()
![]()
![]()
![]()
![]()
![]() .
(9.100)
.
(9.100)
Решение будет зависеть от характера изменения температуры стенки Тст(х), но в общем случае оно получается в виде бесконечного ряда.
Рассмотрим
вначале самый простой для решения задачи
случай, когда температура стенки в
области стабилизированного теплообмена
меняется по линейному закону, что
соответствует условию постоянства
потока тепла, подводимого к теплоносителю
или отводимого от него через стенку
![]() =
const. Из уравнения теплового баланса для
участка трубы длинойх,
учитывая, что отводимый от теплоносителя
тепловой поток в цилиндрической системе
координат будет положительным, следует,
=
const. Из уравнения теплового баланса для
участка трубы длинойх,
учитывая, что отводимый от теплоносителя
тепловой поток в цилиндрической системе
координат будет положительным, следует,
![]()
или ![]() ,
(9.101)
,
(9.101)
 ,
(9.102)
,
(9.102)
т. е. средняя температура теплоносителя в этом случае линейно изменяется вдоль оси х. Для области стабилизированного теплообмена характер радиального изменения температуры остается неизменным, из чего следует
![]() т.е.
т.е.
 .
(9.103)
.
(9.103)
Получим
теперь решение уравнения (9.99) для области
стабилизированного теплообмена при
![]() = const.
Проинтегрируем уравнение (9.99) с учетом
(9.103) и (5.62):
= const.
Проинтегрируем уравнение (9.99) с учетом
(9.103) и (5.62):
 (9.104)
(9.104)
 .
(9.105)
.
(9.105)
Константу интегрирования С можно определить из условия (9.100):
![]()
![]()
![]()
![]() .
(9.106)
.
(9.106)
При r = R выражение (9.105) должно равняться тепловому потоку через стенку, что позволяет получить соотношения для профиля теплового потока (рис. 9.9 а):
 ,
(9.107)
,
(9.107)
 .
(9.108)
.
(9.108)
Проинтегрировав уравнение теплового потока, можно найти профиль температуры в сечении трубы:
 ,
(9.109)
,
(9.109)
или
для безразмерной температуры
![]() (r)
(рис. 9.9 б)
(r)
(рис. 9.9 б)
 .
(9.110)
.
(9.110)
Из
(9.109) и (9.91) можно определить среднюю
температуру
![]() ,
а затем и коэффициент теплоотдачи:
,
а затем и коэффициент теплоотдачи:
 ,
(9.111)
,
(9.111)
![]() ,
(9.112)
,
(9.112)
![]() ,
(9.113)
,
(9.113)
![]() .
(9.114)
.
(9.114)
Решив совместно (9.111), (9.109), и (9.102), можно найти явный вид поля температуры Т(х,r):
 .
(9.115)
.
(9.115)
Таким образом, все величины, характеризующие стабилизированный теплообмен, для рассматриваемого случая определены: поля температуры и теплового потока, коэффициент теплоотдачи. Нетрудно видеть, что средняя температура меняется линейно по длине трубы, а коэффициент теплоотдачи остается постоянным. Следует отметить зависимость лишь от коэффициента теплопроводности теплоносителя и диаметра трубы. От скорости движения теплоносителя он не зависит, что приводит к постоянству критерия Нуссельта.
Теперь рассмотрим стабилизированный теплообмен при постоянной температуре стенки трубы Тст = const. Для него условия (9.102) и (9.103) не выполняются. Это не позволяет вынести за знаки интегрирования T/x в (9.104) и получить явный вид решения. Гретцем, а затем независимо Нуссельтом решение данной задачи было найдено в виде суммы бесконечного ряда. Оно справедливо и для участка термической стабилизации при условии предварительной гидродинамической стабилизации потока. Для области стабилизированного теплообмена локальный коэффициент теплоотдачи равен предельному (рис. 9.7)
![]() (9.116) или
(9.116) или
![]() (9.117)
(9.117)

Рис.
9.7. Изменение локального
![]() и
среднего
и
среднего![]() критериев
Нуссельта по длине круглой трубы
Тст = const:
1
критериев
Нуссельта по длине круглой трубы
Тст = const:
1
![]()
![]() ,
2
,
2![]()
![]()
Средняя температура, как это было показано в разделе 4.1 (4.27), в этом случае изменяется по длине трубы экспоненциально, приближаясь к температуре стенки при х (рис.9.8). Как видим, граничные условия существенным образом влияют на коэффициент теплоотдачи и характер теплообмена, несмотря на то, что дифференциальное уравнение одно и то же (9.99).
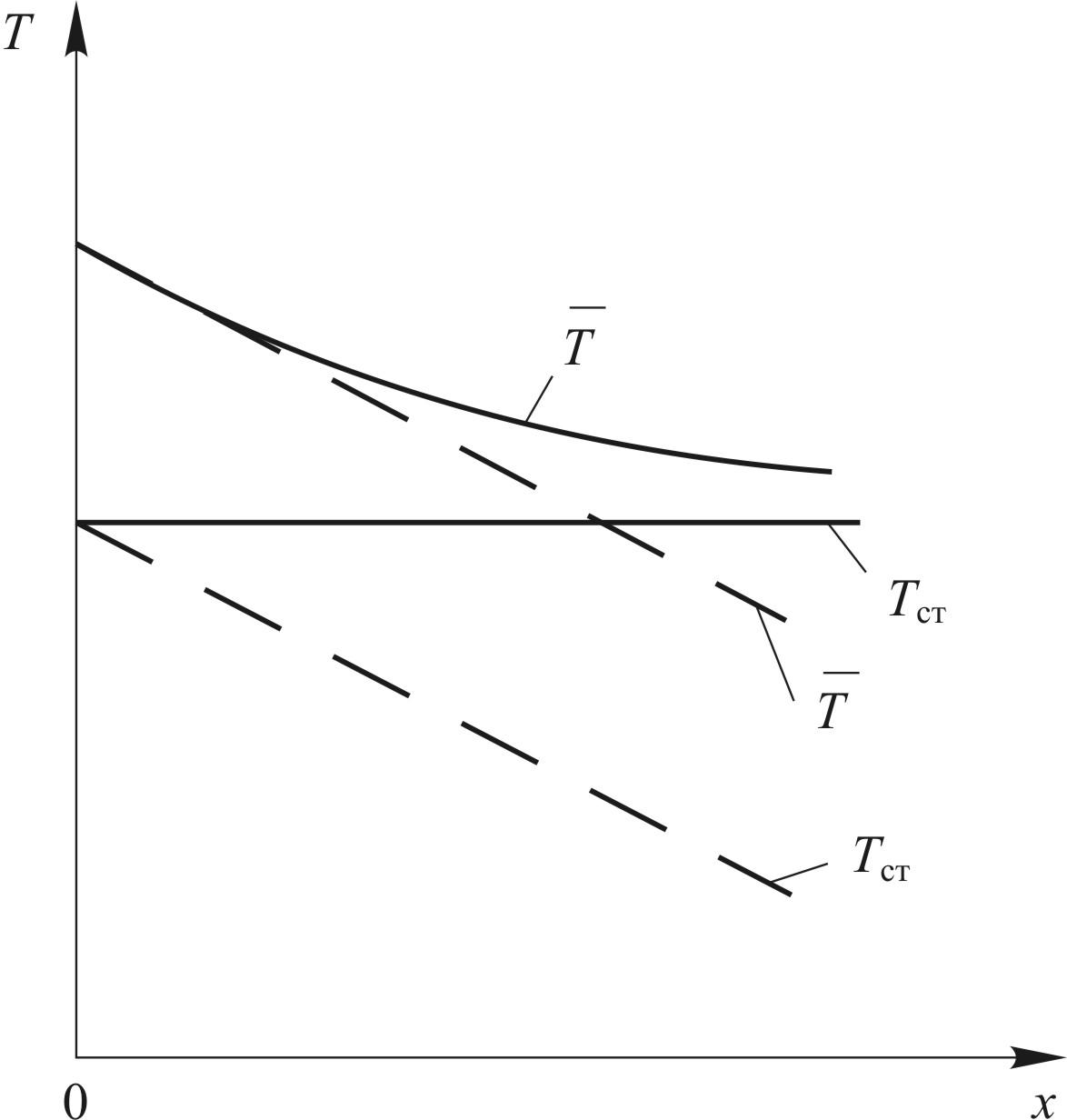
Рис.
9.8. Изменение средней температуры
![]() и
температуры стенки
Тст
по длине
круглой трубы при Тст=const
(—)
и
и
температуры стенки
Тст
по длине
круглой трубы при Тст=const
(—)
и
![]() =const
(- - -)
=const
(- - -)
Для
получения явного вида радиальной
зависимости
![]() можно аппроксимировать ее полиномом
третьей степени, определив три коэффициента
из уравнения (9.117) и граничных условий
можно аппроксимировать ее полиномом
третьей степени, определив три коэффициента
из уравнения (9.117) и граничных условий![]() (0) = 1,
(0) = 1,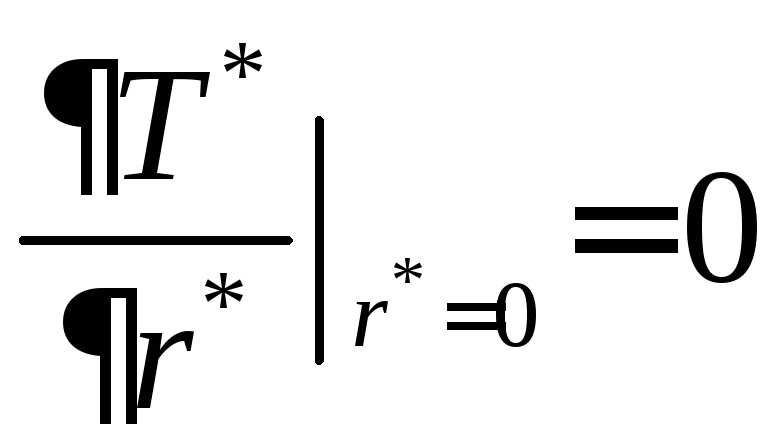 :
:
 (9.118)
(9.118)
Расхождение (9.118) с точным решением не превышает 5% (рис. 9.9 б). Используя (9.118), найдем профиль приведенного теплового потока (рис. 9.9. а):
![]() .
(9.119)
.
(9.119)

Рис.
9.9. Радиальная зависимость в круглых
трубах: a
– относительных потоков тепла
![]() и импульса
и импульса![]() ;
б – относительных температур
;
б – относительных температур![]() и скоростей
и скоростей![]()
С учетом (4.28) можно получить явный вид поля температуры для стабилизированной области:
 ,
(9.120)
,
(9.120)
где
![]() (x1)
– средняя температура в сечении трубы,
расположенном в области стабилизированного
теплообмена на расстоянии x1
от входа.
(x1)
– средняя температура в сечении трубы,
расположенном в области стабилизированного
теплообмена на расстоянии x1
от входа.
Соотношение
для расчета среднего коэффициента
теплоотдачи при Tст = const
для трубы длиной
![]() ,
содержащей участки термической
стабилизации и стабилизированного
теплообмена, с учетом (9.90), (9.96) и (9.117)
можно записать
,
содержащей участки термической
стабилизации и стабилизированного
теплообмена, с учетом (9.90), (9.96) и (9.117)
можно записать
 .
(9.121)
.
(9.121)
В
заключение отметим, что вследствие
различия дифференциальных уравнений,
описывающих перенос импульса и энергии
(5.45) и (9.99) при вынужденном ламинарном
движении в трубе, не наблюдается аналогии
процессов импульсо- и теплоотдачи:
Nuг = 8
Nuт = 4,36
(qст = const),
Nuт=3,66
(Тст = const);
даже при Pr = 1 профиль температур
![]() (r)
неидентичен профилю скорости
(r)
неидентичен профилю скорости
![]() (рис. 9.9б).
(рис. 9.9б).
Стабилизированный
теплообмен при турбулентном движении.
Общий вид
уравнения, описывающего стабилизированный
теплообмен в трубе при турбулентном
режиме движения, будет полностью
идентичным (9.99) примененному нами для
теплообмена с ламинарным потоком.
Сохранятся и граничные условия (9.100).
Отличие будет лишь в тепловом потоке
![]() ,
который включит в себя турбулентную
составляющую переноса тепла. Рассмотрим
вначале теплообмен при условии постоянства
теплового потока по всей поверхности
трубы
,
который включит в себя турбулентную
составляющую переноса тепла. Рассмотрим
вначале теплообмен при условии постоянства
теплового потока по всей поверхности
трубы![]() = const.
Выражения (9.102) и (9.103), полученные для
ламинарного теплообмена, остаются в
силе и для турбулентного. Отличия
возникнут при интегрировании уравнения
(9.99) за счет различных профилей скорости
ламинарного и турбулентного потоков.
= const.
Выражения (9.102) и (9.103), полученные для
ламинарного теплообмена, остаются в
силе и для турбулентного. Отличия
возникнут при интегрировании уравнения
(9.99) за счет различных профилей скорости
ламинарного и турбулентного потоков.
Использовав соотношение (5.88) для всего сечения трубы в пренебрежении отличия поля скорости в узком вязком подслое, подставив его в (9.104), получим (рис. 9.9а)
 .
(9.122)
.
(9.122)
Учитывая,
что
 и при турбулентном течении в трубеcf < 0,01,
можно пренебречь в уравнении (9.122) членами
с соответствующим множителем. Тогда
получим (рис. 9.9 а)
и при турбулентном течении в трубеcf < 0,01,
можно пренебречь в уравнении (9.122) членами
с соответствующим множителем. Тогда
получим (рис. 9.9 а)
![]() .
(9.123)
.
(9.123)
Аналогичный вид имеет в трубе поле потока импульса. Сделанное приближение позволяет получить гидродинамическую аналогию теплообмена при турбулентном течении в трубе в отличие от ламинарного, где она не соблюдается. Необходимо отметить, что в данном случае аналогия является приближенной.
Найдем
выражение для коэффициента теплоотдачи
,
при определении которого в качестве
характерной величины использована в
(9.92) вместо среднемассовой температуры
![]() температура на оси трубыТ(0).
По аналогии с турбулентным тепловым
пограничным слоем на пластине выделим
области изменения суммарного коэффициента
теплопроводности и профиля температуры.
Только в данном случае их будет не
четыре, а три, так как область
логарифмического изменения температуры
может быть распространена вплоть до
оси трубы:
температура на оси трубыТ(0).
По аналогии с турбулентным тепловым
пограничным слоем на пластине выделим
области изменения суммарного коэффициента
теплопроводности и профиля температуры.
Только в данном случае их будет не
четыре, а три, так как область
логарифмического изменения температуры
может быть распространена вплоть до
оси трубы:
![]()
![]() ,
(9.124)
,
(9.124)
![]()
![]() ,
(9.125)
,
(9.125)
![]()
![]() .
(9.126)
.
(9.126)
Найдем в соответствии с (4.9):
 .
(9.127)
.
(9.127)
Используя (5.97), (5.102), (9.76), получим
 .
(9.128)
.
(9.128)
Проинтегрировав
выражение для теплового потока, можно
найти профиль температуры, аналогичный
(9.85)![]() (9.87).
В этих соотношениях нужно использовать
Т(0)
вместо Т0
и расширить верхний предел для y
до R
вместо 0,2г
в (9.87). Уравнение (9.88) будет отсутствовать
(рис. 9.9б). Чтобы перейти к обычно
применяемому для труб коэффициенту
теплоотдачи
(9.87).
В этих соотношениях нужно использовать
Т(0)
вместо Т0
и расширить верхний предел для y
до R
вместо 0,2г
в (9.87). Уравнение (9.88) будет отсутствовать
(рис. 9.9б). Чтобы перейти к обычно
применяемому для труб коэффициенту
теплоотдачи
![]() (9.92), необходимо
определить среднюю температуру
(9.92), необходимо
определить среднюю температуру
![]() .
Подставив (9.85)-(9.87) в (9.91) и пренебрегая
членами, содержащими сомножитель
.
Подставив (9.85)-(9.87) в (9.91) и пренебрегая
членами, содержащими сомножитель![]() ,
получим
,
получим
 .
(9.129)
.
(9.129)
Решая совместно (9.128) и (9.92), найдем
 .
(9.130)
.
(9.130)
Используя
(5.99), (5.102) и (4.75), нетрудно получить критерий
т-г,
характеризующий гидродинамическую
аналогию теплоотдачи. Выражение для
него будет полностью идентично (9.82)
найденному для турбулентного пограничного
слоя на плоской пластине. Отличие будет
заключаться лишь в соотношении для
определения коэффициента трения Фаннинга
![]() (для трубы
можно применять 5.102). Если же с целью
получения явного вида
(для трубы
можно применять 5.102). Если же с целью
получения явного вида
![]() воспользоваться степенной зависимостью
1/7 и формулой Блазиуса (5.105), то
воспользоваться степенной зависимостью
1/7 и формулой Блазиуса (5.105), то
 .
(9.131)
.
(9.131)
Ряд исследователей отмечает консервативность турбулентных течений, которая заключается в слабом влиянии граничных условий на коэффициенты трения и теплоотдачи. Экспериментальные исследования, в частности, подтверждают возможность использования соотношений (9.130), (9.82), (9.131) для расчета коэффициентов теплоотдачи не только при qст = const, но и приTст = const. Подставив (9.131) и (5.108) в (4.75), можно увидеть, что в области стабилизированного теплообмена критерий Нуссельта и коэффициент теплоотдачи при турбулентном течении в трубе в отличие от ламинарного существенно зависят от скорости движения теплоносителя, а точнее, от критериев Re и Pr.
Для анализа удобнее воспользоваться формулой Нуссельта, применимой при 0,5 < Pr < 25 и не очень высоких Re:
![]() или
или
 .
(9.132)
.
(9.132)
Как
и для ламинарного движения, в области
стабилизированного теплообмена при
турбулентном течении локальный
коэффициент теплоотдачи не зависит от
продольной координаты х.
Для расчета среднего коэффициента
теплоотдачи коротких труб (![]() /d < 50)
необходим учет участка термической
стабилизации. Это осуществляется обычно
умножением правой части соотношений
(9.130)
/d < 50)
необходим учет участка термической
стабилизации. Это осуществляется обычно
умножением правой части соотношений
(9.130)![]() (9.132)
на поправочный множитель
(9.132)
на поправочный множитель![]() ,
значения которого приведены в справочных
таблицах.
,
значения которого приведены в справочных
таблицах.
