
10623
.pdf
- 120 -
M max= ql2 / 2 = 20кН×м; Q max= ql = 20кН.
Для стальной балки размеры поперечного сечения находим из условия
прочности по нормальным напряжениям (7.3):
W³ M maxx /[s] = 20 /160 ×103 ×м3= 0,125 ×10−3 м3=1125 см3.
Всортаменте материалов этому условию отвечает двуутавр №18 со сле-
дующими характеристиками сечения: W =143см3; J = 1290 см4; статический момент полусечения S = 81,4 см3; толщина стенки d = 5,1 мм.
Максимальные касательные напряжения в таком двутавре по формуле (7.2) будут равны:
tmax= Q max S /(dJ ) = 20 ×81,4 ×10−6 /(0,51×10−2 ×1290×10−8 ) = 2,475×104 кПа =
=24,75 МПа£ [t] =100 МПа,
т.е. балка имеет четырехкратный запас прочности по касательным напряжением.
Для деревянной бал ки квадратного поперечного сечения со стороной b момент сопротивления W = b3 / 6 и условие (7.3) примет вид:
b3 / 6 ³ M max /[s]= 20 /(16 ×103 ) м3 = 1250 см3,
откуда b ³ 3  6 ×1250 = 19,6 см.
6 ×1250 = 19,6 см.
Округляя до ближайшего размера, рекомендованного в сортаменте пиломатериалов, принимаем b = 20 см.
Статический момент полусечения такого бруса:
S = F0 × yc = 20 ×10 × 5 = 1000 см3,
а момент его инерции:
J = b4 /12 =13333см4.
Подставляя в (7.2), получим:
tmax= Q max S /(bJ ) = 20 ×103 /(20 ×13333) кН×см-2 = 1/1333 3) ×104 МН×м-2 =
=0,75 МПа< [t] = 1,6 МПа,
- 121 -
т.е. условие прочности выполняется. |
∙ |
ГЛАВА 8. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ
8.1. Дифференциальные зависимости при изгибе
Умение определять перемещения необходимо для расчета на жесткость статически определимых систем и является составной частью расчета на прочность систем статически неопределимых. Для обоснования соответствующей методики вернемся к рассмотрению некоторых формул, полученных ранее.
Дополняя дифференциальные зависимости Журавского из параграфа 3.2:
q = dQ / dz |
(3.1)´ |
Q = dM / dz |
(3.2)′ |
соотношениями из параграфов 5.2 и 5.3: |
(5.1)′ |
θ = dv / dz , |
|
M = EJd 2v / dz2 , |
(5.2)′ |
получим следующую цепочку формул, расположенных в зависимости от порядка производной функции прогибов v(z) :
v′ = θ; |
(а) |
|
v′′ = θ′ = M / EJ ; |
|
|
(б) |
(8.1) |
|
v′′′ = θ′′ = M ′ / EJ = Q / EJ ; |
|
|
(в) |
|
|
v′′′′ = θ′′′ = M ′′ / EJ = Q′ / EJ = q / EJ. |
|
|
(г) |
|
Эти соотношения и носят название дифференциальных зависимостей при изгибе.
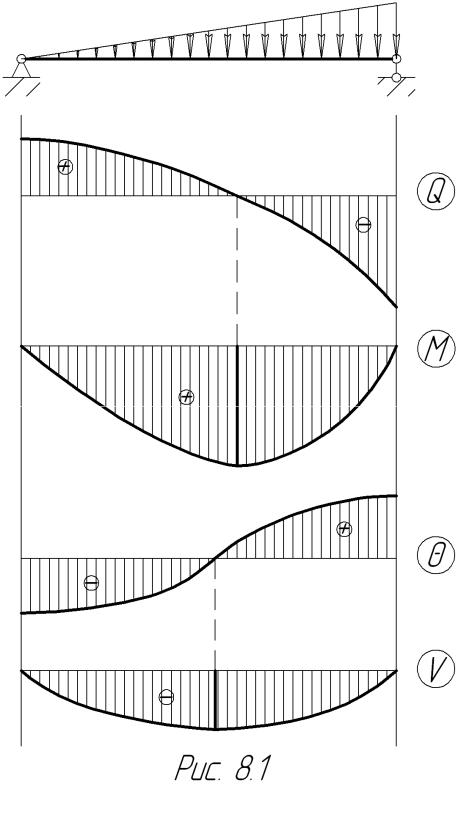
Для того чтобы наглядно представить эти зависимости, рассмотрим балку, загруженную изменяющейся по линейному закону распределенной нагрузкой (рис.8.1). Эпюры, соответствующие (8.1) и приведенные ниже на этом рисунке, имеют следующие особенности:
–максимальное по модулю значение прогибов соответствует нулевому значению θ ;
–касательные к эпюре θ на концах балки горизонтальны, поскольку
М(0) = М (l) = 0 ;
–максимальное значение M соответствует нулевому значению Q ;
–касательная к эпюре Q на левом конце балки горизонтальна, так как
Q′(0) = q(0) = 0 ;
– поскольку q(z) линейна, функции Q, M , θ и v представляют собой многочлены от второй до пятой степени соответственно.
Отметим, что, зная только одну функцию − v(z) , по формулам (8.1) можно найти все остальные: Q, M , θ и q , т.е. определить действующую на балку нагрузку и построить расчетную схему самой балки.
- 122 -
На практике чаще возникает необходимость в решении обратной задачи − определении функции v(z) по известным функциям M (z) или q(z) .
-123 -
8.2.Краевая задача изгиба балки
Для того, чтобы найти функцию v(z) по известной функции M (z) , вос-
пользуемся зависимостью (5.9) или аналогичным соотношением (8.1б): |
|
d 2v / dz2 = M (z) / EJ |
(8.2) |
которое называется дифференциальным уравнением изогнутой оси балки.
Сделаем небольшое отступление и поясним, что означает это понятие. Под дифференциальным уравнением (ДУ) будем понимать зависимость,
связывающую производную от искомой функции v(z) с заданной известной функцией.
Решить ДУ − значит найти функцию v(z) , обращающую эту зависимость в тождество. Порядок производной от функции v(z) определяет порядок диф-
ференциального уравнения.
Рассмотрим следующую задачу: найти решение ДУ первого порядка:
dv / dz = 2z , |
|
|
(8.3) |
удовлетворяющее условию: |
|
|
|
v(0) = 2 . |
|
|
(8.4) |
Очевидно, что решением (8.3) будет не одна, а целое множество функций, |
|||
образующих однопараметрическое семейство: |
v(z) = z2 + C |
, где |
C − постоян- |
|
1 |
|
1 |
ная интегрирования. Только одна из них − при C1 = 2 отвечает условию (8.4). Поэтому решением задачи (8.3) − (8.4) будет: v(z) = z2 + 2 .
Нетрудно догадаться, что общее решение ДУ второго порядка (8.2) будет зависеть не от одной, а от двух постоянных интегрирования.
В самом деле, с учетом (8.1а): dv / dz = θ уравнение (8.2) можно переписать в виде:
dq / dz = (1/ EJ )M ( z) ,
или, разделяя переменные, так:
dq = (1/ EJ )M (z) × dz .
Интегрируя, получим:
∫dθ = (1/ EJ)∫M(z)dz, |
|
откуда следует: |
|
θ (z) = (1/ EJ )∫ M (z)dz + C1. |
(8.5) |
Интегрируя еще раз с учетом θ = dv/dz, найдем общее решение ДУ (8.2):
- 124 -
v(z) =(1/ EJ)∫(∫M(z)dz)dz+ C1z + C2 |
(8.6) |
Из полученного множества функций нужно выбрать ту, которая описывает уравнение изогнутой оси конкретной балки. Для этого, как и в рассмотренном выше примере, задают дополнительные требования, которым должна удовлетворять искомая функция. Они отражают условия закрепления балки и представляют собой значения функции прогибов или производной от нее, заданные, обычно, на границе области, занятой балкой, и поэтому называются краевыми или граничными условиями.
Для простой двухопорной балки длиной l эти условия имеют вид:
v(0) = 0; v(l) = 0 ; |
(8.7) |
а для консольной балки, защемленной на левом конце: |
|
v(0) = 0; v′(0) = θ(0) = 0 . |
(8.8) |
Дифференциальное уравнение изгиба балки (8.2), дополненное краевыми условиями (8.7) или (8.8), и образует краевую задачу изгиба балки.
ПРИМЕЧАНИЕ. При определении прогибов статически неопределимых балок, для которых функция M (z) неизвестна, вместо (8.2) приходится рассматривать более общее ДУ четвертого порядка (8.1г):
d 4v / dz4 = q(z) / EJ .
Соответствующее решение этого уравнения зависит от четырех постоянных: |
|
v(z) = (1/ EJ )∫∫ ∫∫ q(z)dzdzdzdz + C1 z3 + C2 z2 + C3 z + C4 |
(8.9) |
и требует задания не двух, как (8.7) или (8.8), а уже четырех краевых условий. |
|
8.3. Метод начальных параметров |
|
Для того, чтобы на практике воспользоваться решением (8.6): |
|
v( z) = (1/ EJ )∫ (M ( z)dz )dz + C1 z + C2 , |
(8.6)′ |
нужно, во-первых, определить постоянные интегрирования C1 и C2 , а во-
вторых, вычислить входящий сюда интеграл. Аналогичное замечание касается и выражения (8.9).
Решение первой задачи упрощается, если выразить константы через начальные параметры v0 , θ0 , M 0 , Q0 , представляющие собой значения соответст-
вующих функций в начальном сечении балки − на ее левом конце. Подставляя z = 0 в (8.5) и (8.6) получим:
C1 = θ(0) = θ0 ; С2 = v(0) = v0 |
(8.10) |
Аналогично выражаются эти константы и в формуле (8.9).
Переходя к вычислению интеграла, входящего в (8.6), вспомним, что для построения эпюр М и Q мы разбивали балку на отдельные участки и для каж-
дого из них функция M (z) имела различный вид. При таком подходе на каж-
- 125 -
дом участке интеграл нужно вычислять отдельно, а затем стыковать полученные кривые, решая для n участков балки систему 2n уравнений.
Гораздо продуктивнее идея, которая заключается в том, чтобы представить функцию M (z) в виде, едином для всех ее участков.
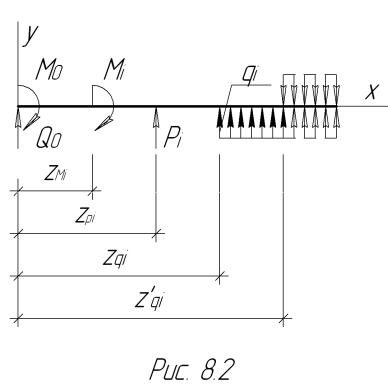
В самом общем случае нагрузку, приложенную к произвольной балке, можно представить так, как показано на рис. 8.2. Будем придерживаться следующих правил при вычислении изгибающего момента в ее сечении:
1)начало отсчета выбирается на левом конце балки, всегда рассматривается часть балки, расположенная слева от сечения;
2)положительные Pi и qi направлены по оси Oy , а моменты M i − по ходу
часовой стрелки, как показано на рисунке;
3) распределенная нагрузка qi , приложенная на участке (z qi , z ′qi ), заменя-
ется той же нагрузкой, продолженной до конца балки, и соответствующей компенсирующей нагрузкой.
При этих условиях изгибающий момент в поперечном сечении любого участка балки можно представить в виде:
M(z) = M +Q z + |
лев[M |
(z − z |
)0 + P(z − z |
pi |
)1 |
+ q (z − z |
qi |
)2 |
/ 2] |
, |
0 0 |
∑ i |
mi |
i |
|
i |
|
|
i
(8.11)
где суммирование распространяется на нагрузку, расположенную слева от рассматриваемого сечения.
В самом деле, для участков балки на рис.8.2 функция M (z) равна:
1) M 0 + Q0 z |
|
(z − z |
|
)0 |
(0 ≤ z < zmi), |
|||||
2) |
M |
0 |
+ Q z + M |
mi |
(z |
mi |
≤ z < z ), |
|||
|
|
0 |
i |
|
|
|
pi |
|||
|
|
|
|
|
|
|
|
- 126 - |
|
|
|
|
3) |
M |
0 |
+Q z + M |
(z − z |
mi |
)0 + P (z − z |
pi |
)1 |
(z |
pi |
≤ z < z ) |
|
|
|
0 |
i |
|
i |
|
|
qi |
||||
и так далее.
Интегрируя дважды последние выражения, на тех же участках балки для
∫∫M (z)dz соответственно получим:
1)M0 z2 / 2 + Q0 z3/ 6 ,
2)M 0 z 2 / 2 + Q0 z 3 / 6 + M i (z − zmi )2 / 2 ,
3)M 0 z 2 / 2 + Q0 z 3 / 6 + M i (z − z mi )2 / 2 + Pi (z − z pi )3 / 6 .
Таким образом, подставляя (8.11) в (8.6), интегрируя дважды и собирая вместе коэффициенты с начальными параметрами, получим,
v(z) = v0 + θ 0 z + M 0 z 2 / 2EJ + Q0 z 3 / 6EJ + |
|
+ (1/ EJ )∑лев [M i (z − zmi )2 / 2 + Pi (z − z pi )3 / 6 + qi (z − zqi )4 / 24] |
(8.12) |
i
Это выражение носит название универсального уравнения изогнутой оси балки.
Из четырех входящих сюда начальных параметров два всегда известны, а два других можно найти из краевых условий или уравнений статики.
ПРИМЕЧАНИЕ. Термин «универсальное» в отношении выражения (8.12) означает, что его форма не зависит от вида нагрузки и числа загруженных участков балки.
Отметим, что это уравнение справедливо для любых типов балок − как статически определимых, так и статически неопределимых.
8.4. Примеры расчета
Рассмотрим примеры определения перемещений в балках с помощью уравнения (8.12). Во всех случаях жесткость балки будем считать заданной.
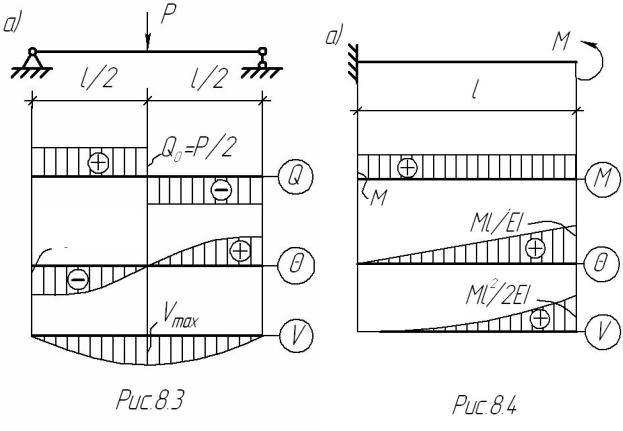
Пример 8.1. Определить максимальный прогиб балки (рис.8.3а). Решение. Три из четырех начальных параметров для нашей балки извест-
ны: v0 = 0, М0 = 0, Q0 = P / 2 , поэтому уравнение (8.12) примет вид:
v(z) = θ0 z + Pz3 /12EJ − (1/ EJ )∑лев |
P(z − l / 2)3 / 6 |
(а) |
|||
Последний параметр θ0 найдем из краевого условия v(l ) = 0 : |
|
||||
0 = θ |
l + Pl3 /12EJ − Pl3 / 48EJ , |
|
|||
0 |
|
|
|
|
|
откуда |
θ |
|
= −Pl2 /16EJ . |
|
|
|
0 |
|
|
||
|
|
|
|
|
|
Подставляя найденные значения θ0 в (а), находим максимальный по модулю прогиб в середине балки:
- 127 - |
|
v(l / 2) = −Pl3 / 32EJ + Pl3 / 96EJ = −Pl3 / 48EJ . |
∙ |
Pl2/16EI
Пример 8.2. Для заданной балки построить эпюры прогибов и углов по-
ворота сечений (рис.8.4а). |
|
|
|
|
|
|
|
|
||
Решение. Нагрузка внутри области, |
занятой балкой (0, l) отсутствует, по- |
|||||||||
этому уравнение (8.12) примет вид: |
|
|
|
|
|
|||||
|
|
v(z) = v + θ |
z + M |
0 |
z2 / 2EJ + Q z3 / 6EJ . |
|||||
|
|
0 |
|
0 |
|
|
0 |
|
||
Два |
начальных параметра |
балки |
|
известны из |
условий закрепления: |
|||||
v0 = v(0) = 0, |
θ0 = v′(0) = 0 , а |
|
|
два других − |
равны |
опорным реакциям: |
||||
М0 = M , |
Q0 |
= 0 , откуда искомое уравнение: |
|
|
||||||
|
|
|
|
|
v(z) = Mz2 / 2EJ . |
|
||||
Дифференцируя, получим: |
|
θ(z) = Mz / EJ . |
|
∙ |
||||||
|
|
|
|
|
|
|
||||
Пример 8.3. Найти максимальные прогибы балки (рис.8.5а). |
||||||||||
Решение. Как и в предыдущем примере |
|
|
||||||||
|
|
v( z ) = v0 + θ 0 z + M 0 z 2 / 2 EJ + Q0 z 3 / 6 EJ , |
||||||||
где М0 = 0, |
Q0 = −P . Для определения неизвестных начальных параметров v0 |
|||||||||
и θ0 нужно воспользоваться краевыми условиями: |
v(l) = 0, θ(l) = 0 . Решая по- |
|||||||||
лученную систему уравнений: |
|
|
|
|
|
|
|
|
||
|
|
v0 + θ0l − Pl 3 / 6EJ = 0; |
|
|||||||
|
|
θ |
0 |
− Pl 2 / 2EJ = 0; |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
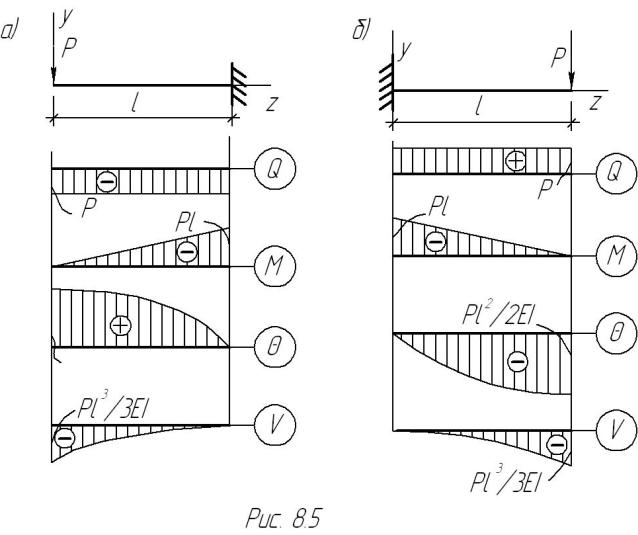
|
|
|
|
- 128 - |
|
найдем: θ |
0 |
= Pl2 |
/ 2EJ , |
v = v max = −Pl3 |
/ 3EJ . |
|
|
|
0 |
|
|
Pl2/2EI
Решение задачи можно упростить, если заданную балку заменить симметрично расположенной (рис.8.5б). Для последней балки все четыре начальных параметра известны: v0 = θ0 = 0 , М0 = −Pl, Q0 = P и уравнение (а) примет
вид:
v(z) = −Plz2 / 2EJ + Pz3 / 6EJ ,
откуда
v max = v(l) = −Pl3 / 3EJ .
Отметим, что все эпюры в заданной балке (рис.8.5а) получаются из эпюр, показанных на рис. 8.5б путем продолжения последних в область отрицательных значений z как симметричных (четных) − v и M либо обратно симметричных (нечетных) − θ и Q. ∙
Пример 8.4. Определить прогиб и угол поворота сечения в середине пролета балки (рис.8.6а).
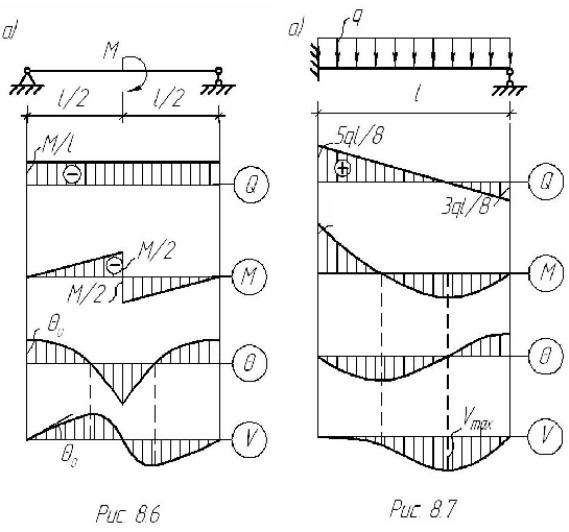
- 129 -
Решение. Три начальных параметра известны либо из условий закрепле-
ния ( v0 = 0, М0 = 0) , либо из уравнений равновесия (Q0 |
= −M / l) , |
поэтому |
||
уравнение (8.12) имеет вид: |
|
|
|
|
v(z) = θ0 z − Mz3 /12EJl + (1/ EJ )∑лев |
M (z − l / 2)2 / 2 |
(а) |
||
Подставляя (а) в краевое условие v(l ) = 0 , найдем θ0 |
= Ml / 24EJ , после |
|||
чего определим искомый |
прогиб: v(l / 2) = 0 . Дифференцируя (а), |
получим: |
||
θ(l / 2) = −Ml /12EJ . |
∙ |
|
|
|
ql2/8
Пример 8.5. Построить эпюры Q и М (рис.8.7а).
Решение. Из условий закрепления левого конца балки v0 = θ0 = 0 , поэтому
v(z) = M |
0 |
z2 / 2EJ + Q z3 / 6EJ − qz4 |
/ 24EJ |
(а) |
||
|
|
|
0 |
|
|
|
Дифференцируя дважды и умножая результат на EJ , получим: |
|
|||||
|
M (z) = M |
0 |
+ Q z − qz2 / 2 |
|
(б) |
|
|
|
|
0 |
|
|
|
Подставляя (а) и (б) в краевые условия: v(l) = 0, М(l) = 0 |
и решая полу- |
|||||
ченную систему уравнений:
