10623

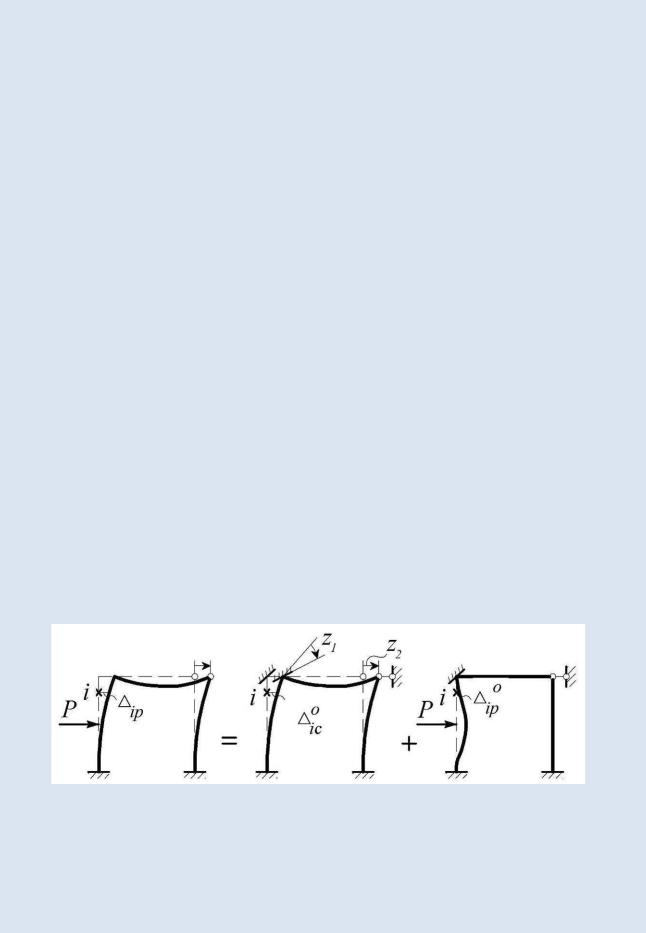
- 230 -

Воспользовавшись принципом суперпозиции, представим эти уравнения в виде:

r11 Z1+ r12 Z2 + R1p0 = 0;

r21 Z1+ r22 Z2 + R2p0 = 0,

где rij − реакция во введенной i-й связи от единичного смещения j-й связи, а Rip0 − реакция в этой связи от заданной нагрузки.

Последние уравнения и называются каноническими уравнениями метода перемещений. В отличие от соответствующих уравнений метода сил эти уравнения имеют не геометрический, а статический смысл.

В общем случае для n неизвестных система канонических уравнений ме-

Решив эту систему и определив неизвестные Zj, можно найти внутренние усилия по формуле, аналогичной формуле (4.7):

Примечание

В соответствии с принципом суперпозиции перемещение любой фиксированной точки i заданной системы можно найти как сумму двух: перемещения этой точки в ОС МП вследствие смещения введенных связей и ее перемещения в той же системе под действием заданной нагрузки (рис. 6.3):

Последнее соотношение является аналогом формулы (6.2) для перемещений.

Рис. 6.3

6.3. Вычисление коэффициентов канонических уравнений

Чтобы определить коэффициенты и свободные члены системы (6.1) нужно предварительно найти эти реакции для отдельных стержней. Соответствую-

- 231 -

щие решения получаются интегрированием дифференциального уравнения изогнутой оси балки или с помощью метода сил и приведены на рис. 6.4, где через i = EJ/l обозначена приведенная жесткость балки.

Рис. 6.4

С помощью этих стандартных решений нетрудно построоить эпюры `Mi0 и

Mp0 в заданной раме. После этого для определения искомых реакций rij и Rip0 достаточно рассмотреть равновесие ее вырезанных узлов или других элемен-

тов, включающих введенные связи.

Пример 6.1. Построить эпюру изгибающих моментов Mp для рамы, рас-

смотренной в примере 4.3. (рис. 6.5, а).

- 232 -

Решение.

1.Отметим, что заданная статически неопределимая система имеет две лишние связи, и при ее расчете методом сил число неизвестных равнялось двум. При решении той же задачи методом перемещений число неизвестных, равное в данном случае числу незакрепленных жестких узлов, будет равно только единице, поэтому в этом примере МП будет эффективнее метода сил.

2.Основную систему МП получаем, вводя моментную связь в этом свободном узле (рис. 6.5, б).

3.Каноническое уравнение метода перемещений имеет вид:

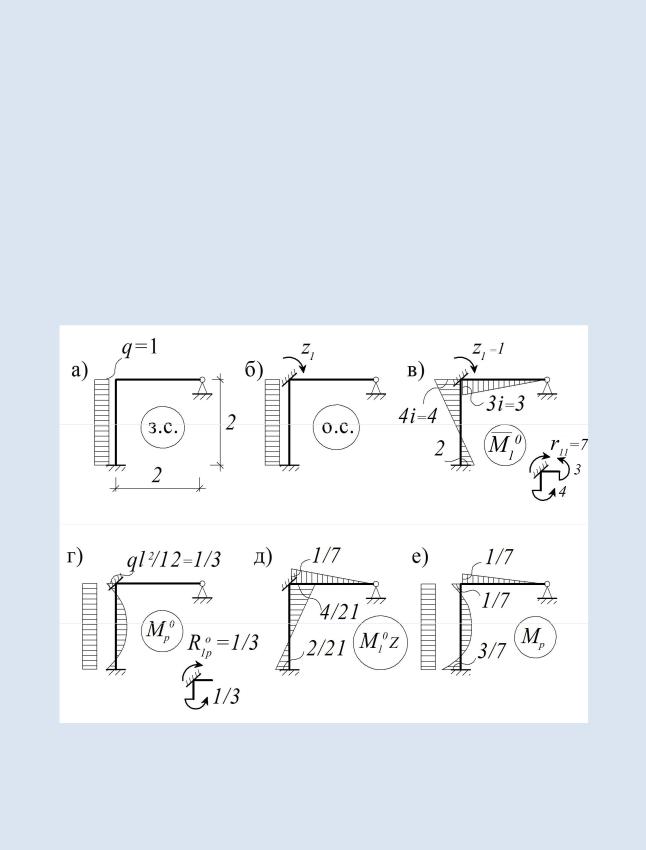
4. С помощью стандартных готовых решений (рис. 6.4) строим эпюры изгибающих моментов от единичного значения Z1 и от заданной нагрузки (рис.

6.5, в, г):

2 3

1

Рис. 6.5

5. Вычисляем r11 и R1p0 , рассматривая равновесие вырезанного второго узла рамы:

-233 -

7.Искомую эпюру изгибающих моментов (рис. 6.5, е) можно построить по формуле (6.2):

Mp = Mp0 + Σ`Mi0Zi.

Нетрудно заметить, что она совпадает с эпюрой, полученной ранее в примере (4.3) с помощью метода сил (рис. 4.5, и). ∙

Примечания

1. Метод перемещений в отличие от метода сил не требует проведения кинематической проверки – достаточно убедиться в равновесии узлов построенной эпюры Mp.

2. Основная система метода перемещений не требует специального выбора – как в методе сил, поэтому МП легко формализуется и удобен для реализации в компьютерных программах.

6.4. Общий метод вычисление коэффициентов

Рассмотренный выше метод вычисления коэффициентов и свободных членов канонических уравнений МП, основанный на рассмотрении равновесия узлов рамы, приводит к затруднениям для рам с наклонными элементами. В этом случае, а также при реализации МП в компьютерной программе целесообразно воспользоваться общим методом вычисления коэффициентов.

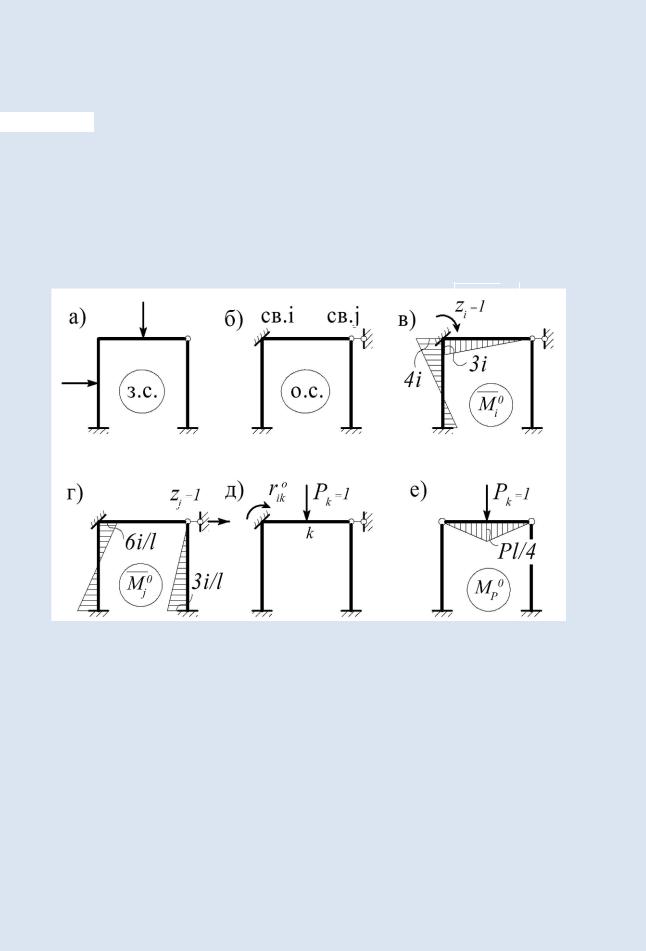
Пусть рама загружена произвольной нагрузкой (рис. 6.6, а), а соответствующая ей основная система МП образована введением двух связей: моментной – i и линейной – j (рис. 6.6, б).

Рассмотрим два состояния этой системы, соответствующие единичным смещениям введенных связей, и обозначим через`Mi0 и`Mj0 соответствующие им эпюры изгибающих моментов (рис. 6.6, в, г).

Вычислим работу внешних сил первого состояния системы на перемещениях второго состояния:

A12 = rii· θij + rji·δjj = rii· 0 + rji·1 = rji .

Учитывая, что в силу (3.15)

A12 = – W12 = – Σ∫(`Mi0 ·`Mj0/EJ ) ds,

получим отсюда искомое выражение для определения удельных реакций:

Последнее выражение напоминает формулу (4.4) для вычисления коэффициентов канонических уравнений в методе сил:

- 234 -

dij = (`Mi0 ´`Mj0) = S∫ (`Mi0 ×`Mj0 /EJ)ds,

и может показаться, что свободные члены системы канонических уравнений в методе перемещений также вычисляются по формуле, аналогичной (4.5):

Dip0= ( `Mi0 ´`Mp0) = S∫ (`Mi0×`Mp0 /EJ)ds.

В действительности это не так: Rip0 ≠ (`Mi0 ´`Mp0), а (`Mi0 ´` Mp0) = 0. Рассмотрим снова два состояния основной системы МП, и пусть первое

по-прежнему соответствует единичному смещению i-й связи (рис. 6.6, в), а второе – единичной силе, приложенной в k-й точке этой системы (рис. 6.6, д).

Рис. 6.6

Работа внешних сил первого состояния системы на перемещениях второ-

го состояния равна нулю:

A12 = rii · θip+ rji · δjp = rii · 0 + rji · 0 = 0,

а поскольку A12 = A21 , то

A21 = P · dpi + rip· θii = 0,

откуда

rip = – d pi .

- 235 -

То есть реакция в i-й связи основной системы от единичной силы, приложенной в точке k , равна взятому со знаком минус перемещению точки приложения силы от единичного смещения этой связи.

Это утверждение носит название второй теоремы Релея.

Возвращаясь к традиционным обозначениям МП и обобщая последнее соотношение на случай нескольких сил произвольной величины, получим:

Таким образом, реакция в i-ой связи ОС МП от заданной нагрузки равна взятой со знаком минус работе всех сил, приложенных к системе, на перемещениях, вызванных единичным смещением этой связи.

Примечание

Поскольку A12 = 0, а A12 = – W12 , то действительно: (`Mi0 ×`Mp0) = – W12 = 0. При этом нетрудно доказать, что искомую реакцию можно вычислить по формуле:

Rip0 = (`Mi0 × Mp0) = – Σ(`Mi0 × Mp0/ EJ)ds,

где `Mi0 – это по-прежнему эпюра моментов в ОС МП от единичного смещения i-й связи, а

Mp0 – эпюра моментов в любой ОС МС от заданной нагрузки. Такой, например, является эпюра, приведенная на рис. 6.6, е.

Легко убедиться, что в этом случае значение Rip0 = – 3 Pl/16 совпадает с табличным значением, указанным на рис. 6.4.

- 236 -

ГЛАВА 7. ПОНЯТИЕ О РАСЧЕТЕ СНС МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ

7.1. Суть метода конечных элементов

Метод конечных элементов (МКЭ) является обобщением рассмотренного выше метода перемещений на двух- и трехмерные системы. Он успешно применяется для расчета самых разнообразных строительных конструкций и сооружений, в том числе – тонкостенных систем и массивов.

В отличие от классических форм МС и МП МКЭ является компьютерным методом. Он появился в 60-е годы прошлого века и в настоящее время является самым распространенным методом расчета, реализованным в большинстве систем автоматизированного проектирования.

Особенность метода в том, что он позволяет решать задачи теории упругости методами строительной механики.

Реализация МКЭ включает следующие этапы:

1)разбиение конструкции на конечные элементы с учетом ее геометрии, физических свойств материала и нагрузки;

2)анализ отдельного конечного элемента (КЭ), в ходе которого строится

матрица жесткости КЭ – [ Rэ] и определяется вектор приведенной узловой нагрузки – { Pэ};

3) анализ всей конструкции и формирование системы конечноэлементных уравнений:

где [R], {Z} и {P} – соответственно матрица жесткости, вектор неизвестных и вектор приведенной узловой нагрузки всей системы;

4)решение системы уравнений и определение по вектору {Z} напряжений

иусилий в отдельных конечных элементах.

Отметим, что под конечным элементом понимают часть конструкции, которая обладает всеми ее физическими свойствами и имеет несколько фиксированных узловых точек с введенными в них связями, которыми КЭ связаны друг с другом.

Уже к 70-м годам прошлого века была создана хорошо апробированная система конечных элементов, приспособленных для решения самых разнообразных задач.

При решении плоской задачи и задачи изгиба пластин и плит применяют треугольные и прямоугольные КЭ с различным числом степеней свободы. Для решения трехмерных задач применяют КЭ в виде параллелепипеда или тетраэдра. Разработаны конечные элементы для решения осесимметричных задач и целое семейство плоских и криволинейных КЭ для расчета оболочек.

МКЭ прекрасно приспособлен для решения практических задач и позволяет с высокой степенью точности аппроксимировать границу области, занятой

- 237 -

телом. Помимо строительной механики и теории упругости МКЭ находит применение в решении широкого круга задач математической физики.

7.2. Применение МКЭ для расчета стержневых систем

Расчет стержневых систем с помощью МКЭ приводит к тем же уравнениям, что и обычный метод перемещений, хотя подходы к их построению немного отличаются по форме.

При этом КЭ рамы с 6-ю степенями свободы имеет на концах два узла, в каждом из которых введено по три связи – две линейных и одной моментной.

Его матрица жесткости имеет 6-й порядок, а ее элементами являются реакции rij в шести введенных связях от единичных смещений этих связей.

Компонентами вектора приведенной узловой нагрузки являются взятые со знаком минус реакции во введенных связях от приложенной к КЭ нагрузки,

которые, в отличие от МП, будем обозначать не Rip0 , а rip0:

{Pэ}= – [ r1p0, r2p0, … , r6p0]Т,

где индексом «т» обозначена операция транспонирования.

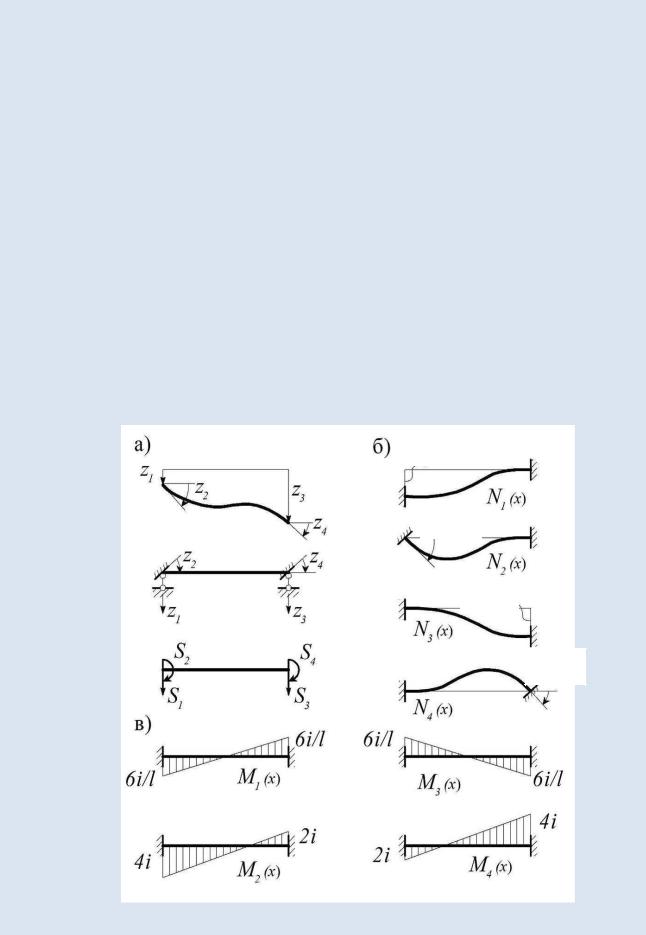
Балочный конечный элемент, на примере которого мы рассмотрим процедуру анализа, имеет только четыре степени свободы. В качестве неизвестных такого КЭ выбирают неизвестные прогибы и углы поворотов в начальном и конечном сечениях, как и в обычном методе перемещений (рис. 7.1, а).

Анализ КЭ заключается в определении реакций во введенных связях

{Sэ}= [S1, S2, S3, S4]Т от кинематических воздействий {Zэ}= [Z1, Z2, Z3, Z4]Т и от действующей местной нагрузки. Первая зависимость имеет вид:

{Sэ} = [Rэ]{Zэ}.

Для построения матрицы жесткости [Rэ] рассмотрим КЭ при единич-

ных кинематических воздействиях (рис. 7.1, б), объединив соответствующие им функции формы в матрицу-строку:

[N] = [N1(x), N2(x), N3(x), N4(x)].

Этим функциям формы соответствуют уже известные эпюры моментов, приведенные на рис. 6.4 и 7.1, в, которые также объединим в вектор:

{M} = [M1(x), M2(x), M3(x), M4(x)]Т.

Учитывая, что для принятой системы координат зависимость между изгибающими моментами и прогибами имеет вид:

M(x) = – EJ v''(x),

- 239 -

Поэтому, дополнив соотношение (6.5) работой распределенной нагрузки, приложенной к КЭ, и сменив обозначения, получим:

rip0 = – [ Σ Pk · Nik + ∫ q(x) · Ni (x) dx].

Таким образом, искомый вектор приведенной узловой нагрузки равен:

Как видим, анализ КЭ сводится в конечном итоге к построению матрицы функций формы. Помимо методов, упомянутых в параграфе 6.3, эти функции можно, например, построить следующим способом.

Представим уравнение изогнутой оси КЭ в виде полинома:

где [H] = [1, x, x2, x3], а {a} = [a1, a1, a1, a1]Т.

Приравнивая (7.4) и (7.6) в узловых точках КЭ, то есть при x1 = 0 и x2 = l, получим:

Z1 = v (0) = 1 + a1x1+ a2x12+ a3x13 ;

Z2 = v'(0) = a1+2a2x1+ 3a3x12 ;

Z3 = v (l) = 1 + a1x2 + a2x22 + a3x23 ;

Z4 = v'(l) = a1 +2a2x2+ 3a3x22,

или иначе

{Zэ} = [L] {a},

где [L] = [[H(x1)]T, [H'(x1)]T, [H(x2)]T, [H'(x2)]T]Т.

Обратная зависимость

{a} = [L]–1 {Zэ}

после подстановки в (7.6) приводит с учетом (7.4) к искомой формуле:

В скалярной форме последняя зависимость имеет вид:

N1(x) = 1 – 3 ξ2 + 2 ξ3;

N2(x) = l (ξ – 2 ξ2 + ξ3);

N3(x) = 1 – 3 η 2 + 2η3;

N4(x) = l (– η + 2η 2 – η 3),

где ξ = x/l , η = (l – x)/l .