10614

1.5 . Метод сечений. Напряжения

Для расчета на прочность нужно знать, какие силы появляются в каждой внутренней точке тела в ответ на действие внешних сил. Для их определения воспользуемся обобщением принципа освобождаемости от связей из ТМ, сделав внутренние силы внешними.

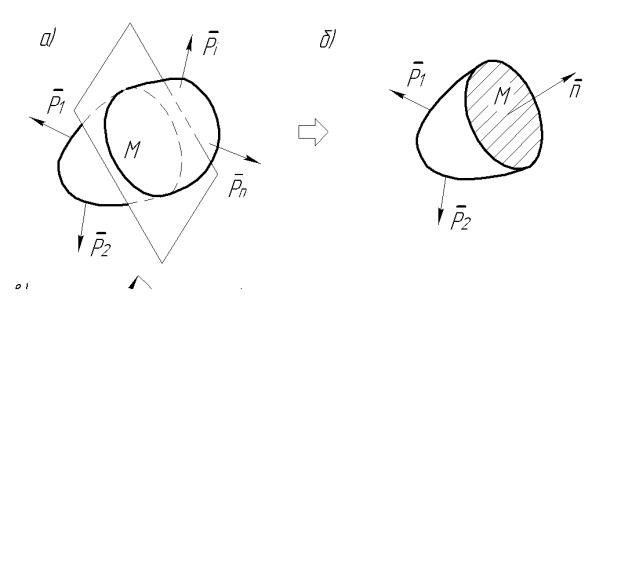
Рассмотрим тело под действием уравновешенной системы сил (рис. 1.8а). Проведем через интересующую нас точку М плоскость и рассмотрим часть тела слева от сечения с нормалью n (рис. 1.8б). Помим о внешних сил Р1 и Р2 на нее будет действовать реакция отброшенной право й части, не показанная на рисунке. Эту реакцию в виде распределенной по площади сечения поверхностной нагрузки и будем называть напряжением.

Выясним, чем отл ичается напряжение от обычного давления. Как известно из ТМ, реакция связи направлена в сторону, противоположную той, куда тело не может перемещаться из-за наложенной связи. Поэтому если бы напряжение, как и давл ение, было направлено по нормали n, части тела, расположенные по обе сто роны от плоскости воображаемого с ечения, могли бы беспрепятственно смещаться друг относительно друга вдоль этой плоскости. Наш опыт свидетельствует об обратном, поэтому можно сделать вывод, что в

общем случае напряжение является вектором, который направлен под углом к нормали n в каждой точке сечения.

Разложим вектор напряжения p по правилу параллелограмма на нор-

мальную и касательную составляющие:

p = σ + τ,

где σ || n, а τ n.

Эти напряжения мо жно наглядно показать на рисунке, если рассмотреть тело в плоскости, ортогон альной к проведенному сечению. Поскольку при этом все векторы τ будут расположены вдоль одной прямой, их в личины в каждой точке сечения условно откладывают в направлении нормали n (рис. 1.8 в-д).

Последовательней и удобней заменить построение векторов σ и τ построением эпюр их проекций на эту нормаль и перпендик улярные к ней направления, как и принято в СМ.

Эти напряжения и нужно знать для расчета тела на прочность. Как их найти? Для тел простой формы − из условий равновесия отсеченной части, как обычно в ТМ находят реакции опор. При этом, в соответствии с принципом отвердевания, мо жно воспользоваться теоремой о приведении пространственной системы сил, согласно которой произвольная система сил эквивалентна главному вектору R0 и главному моменту M0:

(Р1, Р2, …, Рn) (R0, М0).

ПРИМЕЧАНИЯ:

1.В СМ нередко отождествляют понятия вектора напряжения и его проекции, говоря об «эпюре напряжений» или о «положительном направлении» этого вектора.

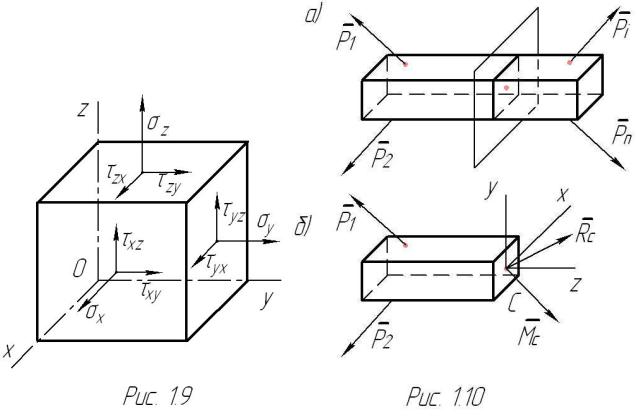
2.Если тремя парами параллельных плоскостей вырезать из тела куб, то напряжения, действующие по его граням и соответствующие положительным значениям их проекций, в общем случае можно обозначить так, как показано на рис. 1.9. В дальнейшем для касательных напряжений нам будет удобнее изменить эти направления на противоположные.

3.Мы предполагаем, что напряжения в сечении тела могут появляться только в ответ на действие внешних сил, и равны нулю при их отсутствии, что соответствует гипотезе ненапряженного начального состояния.

1.6. Внутренние усилия в брусе. Виды НДС

Применим рассмотренный в предыдущем параграфе метод сечений к частному случаю тела − брусу, загруженному уравновешенной системой сил (рис. 1.10а). Проведем сечение и рассмотрим равновесие части стержня слева от сечения под действием сил Р1, Р2 и реакций отброшенной правой части или напряжений. Приведем последние к центру, выбрав в качестве

него точку C − центр тяжести сечения.

Введем систему координат с началом в центре C и обозначим через Rc и Mc главный вектор и главный момент реакций отброшенной правой части (рис.

1.10б).

Определение. Внутренними усилиями в стержне называются проекции векторов Rc и Mc на оси координат системы Cxyz, взятые с определенным знаком.

Условие равновесия отсеченной части:

Компоненты этих усилий называются так: Qx, Qy - поперечные силы;

Nz - продольная или нормальная сила; Mx, My - изгибающие моменты;

Mz - крутящий момент.

Внутренние усилия можно выразить не только через внешние силы и их проекции – по формуле (1.1), но и через компоненты вектора напряжения в поперечном сечении бруса с площадью F:

Отметим, что формулы (1.2) справедливы для любой части бруса – как слева, так и справа от сечения. В отличие от этих формул, в (1.1) при переходе к рассмотрению правой части стержня нужно сменить все знаки на противоположные.

В зависимости от значений внутренних усилий различают несколько видов напряженно-деформированных состояний (НДС), некоторые из которых мы рассмотрим.

1. Центральным растяжением и сжатием (ЦРС) называется НДС, при котором Nz ¹ 0, а все остальные внутренние усилия равны нулю. ЦРС возникает в брусе, растягиваемом (сжимаемом) силами, приложенными к его торцам (рис.

1.11а).

2. Чистый изгиб соответствует НДС, при котором обращаются в нуль все компоненты внутренних усилий за исключением Mx (или My). Появляется в брусе при его изгибе двумя моментами, приложенными по торцам (рис. 1.11б).

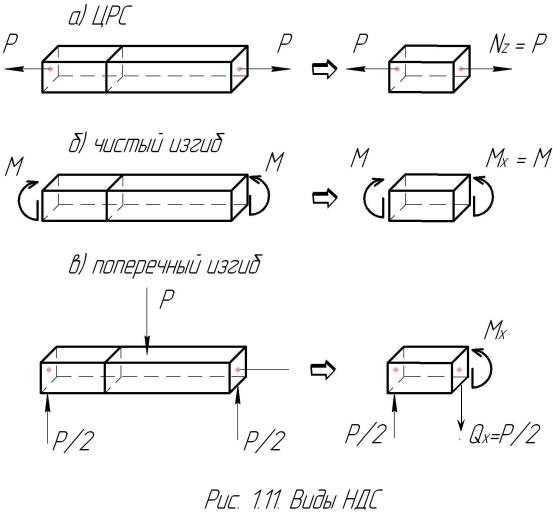
3. Поперечный изгиб – это НДС, при котором Qy ¹ 0, Mx ¹ 0, а остальные компоненты равны нулю. Возникает, например, в брусе, опертом по концам и загруженном посредине силой (рис. 1.11в).

Решение основной задачи СМ для этих НДС бруса и составляет основное содержание данного раздела курса.

ПРИМЕЧАНИЯ:

1.В соответствии с принципом Сен-Венана картина распределения напряжений при ЦРС в поперечном сечении бруса на достаточном удалении от его концов не зависит от способа приложения нагрузки. Это справедливо и для других видов НДС.

2.Внутренние усилия, несмотря на название, не являются силами, противодействующими приложенной нагрузке, – по отношению к рассматриваемой части стержня продольная сила Nz является такой же внешней силой, как и сила Р (рис1.11а).

ГЛАВА 2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ

2.1. Напряжения и деформации

Напряжения. Пусть стержень с площадью поперечного сечения F растягивается двумя равными по модулю силами Р.

Проведем сечение и рассмотрим часть стержня слева от сечения (рис. 1.11а). Действие отброшенной правой части заменим нормальными напряжениями sz, эквивалентными продольной силе Nz = Р.

Предполагая, что нормальные напряжения равномерно распределены по площади поперечного сечения F, получим:

Nz = ∫ sz dF = sz×F,

F

откуда искомое выражение для напряжений при ЦРС примет вид:

Правило знаков. При растяжении стержня: sz > 0, Nz > 0; при его сжатии –

sz < 0, Nz < 0.

Деформации. Обозначим через l длину стержня до деформации, и пусть под действием приложенной нагрузки его длина стала равной l+Dl, где Dl - аб-

солютное удлинение стержня.

Относительным удлинением или продольной деформацией стержня при ЦРС называется величина

Правило знаков. При растяжении: Dl > 0, e > 0; при сжатии: Dl < 0, e < 0.

Вобщем случае продольная сила Nz непостоянна по длине стержня. Например, – при его растяжении или сжатии под действием собственного веса. При этом будут неравномерны удлинения отдельных участков стержня и применение формулы (2.2) теряет смысл.

Для вывода формулы, являющейся обобщением (2.2) на случай переменной продольной силы и неравномерных деформаций, введем понятие перемещения точки деформируемого тела.

Пусть точка A(x, y, z) упругого тела в результате силовых или каких-либо иных воздействий перемещается и занимает в пространстве положение А'.

Вектор AA' (u, v, w) называется перемещением точки А деформируемого

тела.

Вобщем случае каждая компонента вектора перемещения является функцией координат – x, y, z.

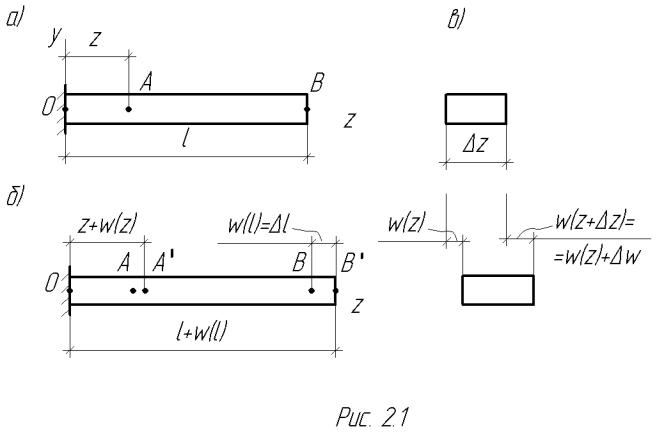
Рассмотрим брус дл иной l в системе координат Oxyz, где начало отсчета

выбрано на его левом, ж естко защемленном конце, плоско сть Oyz является плоскостью симметрии, а ось Оz проходит через центр тяжести сечений.

При этих предпосылках положение точки А, лежащей на оси бруса, однозначно определяется заданием только одной координаты – z (рис. 2.1а).

Под действием сил, приложенных вдоль оси Оz, и вызывающих центральное растяжение стержня, точка А получит перемещениие AA'. Очевидно, что величина перемещения определяется удалением точки А от начала коорди-

нат: w(0) = 0, w(z) = AA′, w (l) = l (рис.2.1б).

Проведем два сечения на расстояниях z и z+ z от левого конца и рассмотрим поведение заключенного между ними участка стер жня в ходе его загружения. Если положить w(z+ z) = w(z) + w, то станет очевидным, что перемещение этого отрезка стержня как твердого тела на величину w(z) сопровождается его удлинением на величину w (рис. 2.1в). Предполаагая, что продольная сила остается постоянной на участке z, воспользуемся формулой (2.2) для определения его относите льного удлинения. Подставляя в (2.2) l = w, а l = z и переходя к пределу, пол учим выражение продольной деформмации в сечении z:

Таким образом, зная w(z) можно найти деформацию εz(z), и наоборот – по известной деформации εz из (2.3) можно найти перемещение w:

2.2. Закон Гука. Коэффициент Пуассона

Вернемся к рассмотрению стержня из предыдущего параграфа и, следуя Р.Гуку, зададимся вопросом: как связаны удлинение стержня – l, его длина – l, площадь поперечного сечения – F и величина приложенной нагрузки – Р ?

Экспериментально была установлена зависимость:

которая известна как закон Гука при ЦРС.

Входящий в эти формулы множитель Е называется модулем упругости или модулем Юнга. Поскольку относительная деформация ε = l / l в (2.6) – безразмерная величина, размерности σ и E совпадают. Приведем значения E для некоторых материалов, применяемых в строительстве:

сталь – 200 ГПа, бетон – 20 ГПа,

дерево вдоль волокон – 10 ГПа.

Чтобы выяснить смысл модуля упругости, отметим, что σ = E при ε = 1.

Таким образом, модуль упругости численно равен напряжению, при котором стержень удваивает свою первоначальную длину. В действительности ни один из материалов, за исключением резины, не выдержит такого напряжения.

Для металлов ε имеет максимальные значения порядка 0,0001÷ 0,001, и их разрушение наступает при напряжении σ, примерно в тысячу раз меньше значения Е.

Как известно, удлинение стержня при ЦРС сопровождается изменением его поперечных размеров. Пусть b – начальная ширина стержня, а b+ b – его поперечный размер при деформации.

Поперечной деформацией называется отношение

ε′ = b/b.

Правило знаков: при растяжении b < 0, ε ′ < 0 ; при сжатии стержня b > 0, ε ′ > 0 .

Коэффициентом Пуассона называется отношение поперечной деформа-

ции стержня к его продольной деформации:

ν = −ε ′ / ε .

Приведем значения ν для некоторых материалов:

сталь – 0,3;

бетон – 0,17;

дерев о вдоль волокон – 0,5.

Теоретические и экспериментально доказано, что 0 ≤ν ≤ 0,5 .

Итак, упругие свойства материалов определяются двумя физическими

константами – Е и ν .

2.3. М еханические испытания материа лов

Для определения постоянных Е, ν и других характери стик материалов, необходимых для расчета, проводят механические испытания их стандартных образцов с заданной длин ой l и площадью поперечного сечения F. В ходе тако-

ε = l / l . С учетом особенностей этих диаграмм σ (ε ) все мате риалы делятся на

два класса:

1)пластичные (сталь, алюминий);

2)хрупкие (стекло, чугун).

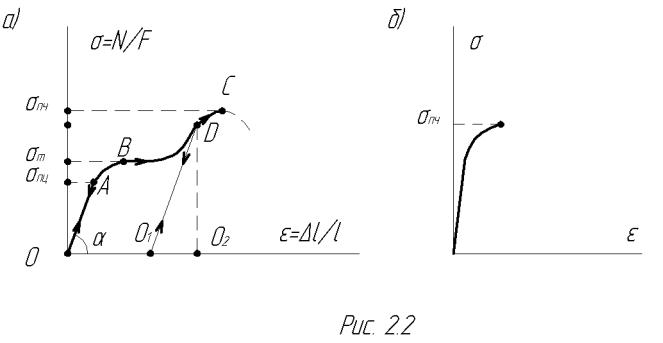
Рассмотрим диаграм му растяжения стального образца, на которой отмечены характерные точки и соответствующие им напряжения ( рис.2.2а).

Пределом пропорциональности (σпц) называется максимальное напряжения, соответствующее точке А диаграммы, при котором сохраняется линейный характер зависимости σ(ε) в соответствии с законом Гука. Сравнивая уравне-

ние прямой ОА: σ = tgα ×ε с (2.6), получим, что Е = tgα .

Пределом текучести (σт) называется напряжение, при котором деформирование образца происходит без увеличения нагрузки, что вызвано перестройкой структуры стали. Горизонтальный участок диаграммы в окрестности точки В называется площадкой текучести.

Предел прочности (σпч) – максимальное напряжение, которое выдерживает образец до разрушения.

Проследим теперь за образцом при уменьшении приложенной к нему нагрузки.

Если в процессе его загрузки напряжение не превысило σпц, то разгрузка происходит по той же прямой ОА, по которой происходило нагружение, и после снятия приложенной нагрузки тело полностью восстановит свои размеры и форму.

Разгрузка из точки D, принадлежащей участку АС, происходит по прямой О1D, параллельной ОА.

Таким образом, полная деформация стержня в точке D – ОО2 складывает-

ся из упругой – О1О2 и пластической или остаточной ОО1.

Поведение хрупких материалов при растяжении характеризуется разрушением в упругой стадии при незначительных деформациях. На диаграмме растяжения таких материалов есть только одна характерная точка, соответствующая σпч (рис.2.2б).

Свойства хрупких материалов, в отличие от пластичных, при растяжении и сжатии различны, поэтому для них строят обе диаграммы. Такие материалы как бетон или кирпич испытывают только на сжатие, т.к. они практически не работают на растяжение.

ПРИМЕЧАНИЯ:

1.В действительности между точками А и В на диаграмме (рис.2.2а) расположена еще одна точка, которой соответствует напряжение предел упругости (σупр), близкое по значению

к(σпц). В рамках этого курса мы будем считать σпц равным σупр.

2.Мы рассмотрели процесс испытания образца и определение свойств материала в самом первом приближении. В действительности характер диаграммы зависит от многих факторов, в том числе – скорости деформирования и температуры проведения испытаний, поэтому для ряда материалов правильнее говорить не об их принадлежности к тому или иному классу, а о проявлении у них соответствующих свойств в определенных условиях.

3.Приведенная диаграмма (рис.2.2а) носит условный характер, т.к. не учитывает изменение первоначальной длины стержня l и площади его поперечного сечения F в ходе испытания и, особенно, на его завершающей стадии. В рамках этого курса не рассматривается механизм разрушения деформируемого тела.