
10614
.pdf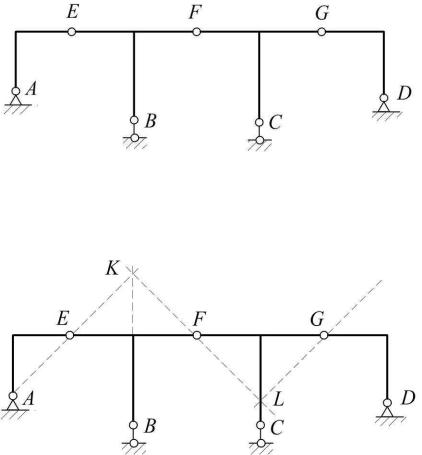
Решение. Воспользуемся методом нулевой нагрузки, применив графический способ решения – см., например, [2], с. 53.
Из условия равновесия диска АЕ (рис. 1.19) следует, что реакции RA и RE направлены по прямой АЕ (аксиома 2).
Рис. 1.18
Рис. 1.19
Из условия равновесия диска EBF следует, что реакция RF проходит через точку K, где пересекаются линии действия R′E = − RE и RB (теорема о трех силах).
Из условия равновесия диска FCG аналогично находим линию действия реакции RG, проходящей вдоль прямой GL.
Наконец, рассмотрим диск DG . По аксиоме 2 реакция RG = − RD должна быть направлена вдоль прямой GD, соединяющей точки их приложения. С другой стороны, R′G = − RG действует по прямой GL. Одновременно удовлетворить этим требованиям можно, лишь полагая RG = 0, откуда следует, что все реакции равны нулю, а значит {X} = {0} и система будет неподвижной. ∙
Примечания
1. Подобно тому как СНС, которые мы рассмотрим в 4-й главе, могут быть статически неопределимыми внешним и внутренним образом, можно говорить о системах, изменяемых
аналогично. Поэтому в общем случае вектор {X} в системе (1.6) должен содержать компоненты реакций не только внешних, но и внутренних связей.
2.Отметим, что в последнем примере 1.4 мы остаемся в рамках аналитического метода анализа геометрической изменяемости системы, несмотря на то, что при реализации метода нулевой нагрузки применялся графический способ определения реакций связей. Такой прием вполне оправдан, поскольку формальный подход потребовал бы вычисления определителя двенадцатого порядка.
3.Анализ системы уравнений (1.6), независимо от условия (1.5), позволяет получить полную характеристику механической системы, в том числе степень ее свободы и степень ее статической неопределимости.
4.При построении модели сооружения ее параметры определяются с некоторой степенью точности, поэтому опасность на практике представляют не только МИС, но и близкие
кним – у которых det [A] ≈ 0.
1.3. Основные уравнения строительной механики
Математическая сторона основной задачи строительной механики основана на зависимостях, полученных в сопромате. Напомним их на примере на- пряженно-деформированного состояния элемента рамы, для которого – в отличие от балки – поперечный изгиб сопровождается дополнительным растяжением или сжатием.
Пусть такой элемент длиной dx расположен в локальной системе координат Oxy, где ось Ox направлена по оси стержня, и загружен распределенной на-
грузкой интенсивностью qx и qy вдоль Ox и Oy соответственно (рис. 1.20). Напряженно-деформированное состояние стержня определяется девятью
компонентами:
–внутренними усилиями (M, Q, N,);
–перемещениями (u, v, θ);
–деформациями (κ, γ, ε).
Уравнения для определения этих функций можно разделить на три груп-
пы.
Статические уравнения – связывают внутренние усилия (рис. 1.20, б) с заданной нагрузкой:
dN/dx = – |
qx; |
|
|
dQ/dx = |
qy; |
|
(1.10) |
dM/dx = |
Q . |
|
|
Геометрические уравнения – выражают деформации через перемещения, показанные на рис. 1.20, в, г:
κ = dθ/dx; |
|
|
|
γ |
= θ − dv/dx; |
|
(1.11) |
ε |
= du/dx. |
|
|
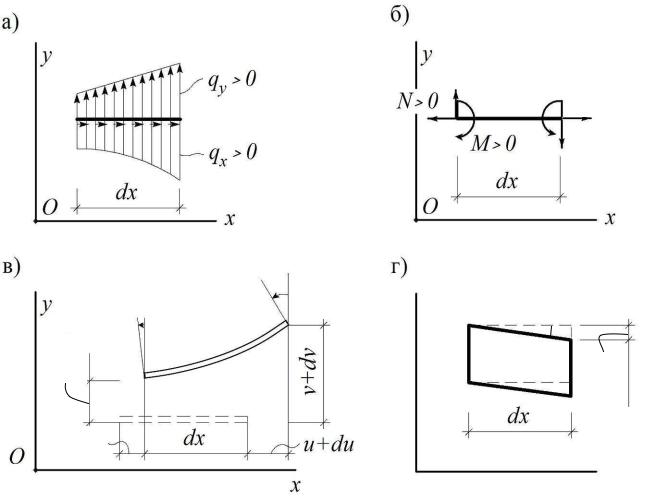
Физические уравнения – представляют собой зависимости между внутренними усилиями и деформациями:
|
κ = M/EJ; |
|
|
|
γ = μQ/GF; |
|
(1.12) |
|
ε = N/EF; |
|
|
где E – |
модуль Юнга; |
|
|
G – |
модуль сдвига; |
|
|
F – |
площадь поперечного сечения стержня; |
|
|
J – |
момент его инерции; |
|
|
μ – |
коэффициент, учитывающий неравномерность распределения каса- |
||
тельных напряжений в поперечном сечении стержня.
v>0
u>0
|
|
|
|
|
Q > 0 M+dM |
|||
|
qy > 0 |
|
|
|
||||
|
|
|
N > 0 |
|
|
|
N+dN |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M > 0 |
Q+dQ |
||
|
qx > 0 |
|
|
|
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
θ+dθ
γ>0
θ>0
dv<0
Рис.1.20
Отметим, что выражения EJ и EF в (1.12) называются жесткостями стержня при изгибе и растяжении (сжатии) соответственно.
При решении системы уравнений (1.10) – (1.12) возможны два варианта:
1)внутренние усилия M, Q, N удается найти из системы уравнений (1.10), не обращаясь к остальным уравнениям – это СОС;
2)внутренние усилия можно найти только путем совместного решения всех девяти уравнений – это СНС.
Впоследнем случае при решении этих уравнений возможны два подхода:
– в качестве основных неизвестных выбирают усилия M, Q, N, выражая
все остальные через них – это решение в форме метода сил;
– в качестве основных неизвестных выбирают перемещения u, v, θ – это
решение в форме метода перемещений.
Системы, описываемые линейными уравнениями (1.10) − (1.12), называются линейно-деформируемыми. Для них справедлив принцип суперпозиции, в соответствии с которым:
внутренние усилия, перемещения и деформации от заданной нагрузки (или иного воздействия) можно найти как сумму соответствующих величин от каждой нагрузки в отдельности.
Примечания
1. Первое из статических уравнений (1.10) получается из условия равновесия рассматриваемого элемента рамы. Полагая в его пределах qx = const, и составляя уравнение SX = 0, получим:
– N + qx×dx + (N +dN) = 0,
откуда и следует искомая зависимость. Два других уравнения из (1.10) – это дифференциаль-
ные зависимости Журавского.
2. Первое из физических уравнений (1.12) представляет собой дифференциальное уравнение изогнутой оси балки:
κ = dq/dx = d 2v/dx 2 = M /EJ.
Второе уравнение в предпосылке равномерного распределения касательных напряжений в поперечном сечении стержня (m =1) выражает закон Гука при сдвиге:
t = Q/F = Gg.
При этом мы не уточняем смысл коэффициента m по причине, которая будет указана в § 3.5. Последнее из физических уравнений (1.12) – это закон Гука при ЦРС:
s= N/F = E×e.
3.В дальнейшем мы будет по-прежнему применять обозначение Oxy для глобальной системы координат, связанной с конструкцией в целом.
ГЛАВА 2. РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ
2.1. Свойства статически определимых систем
Эти свойства определяются тем фактом, что для нахождения внутренних усилий в таких системах достаточно рассмотреть уравнения статики (1.10), не обращаясь к геометрическим (1.11) или физическим (1.12) уравнениям.
1. Внутренние усилия не зависят от геометрии поперечных сечений и материала стержней.
Действительно, физические константы E, G, n и геометрические характеристики сечений F, J не входят в уравнения равновесия (1.10).
2. Температурные и кинематические воздействия не вызывают появления реакций и внутренних усилий в СОС.
В самом деле, эти воздействия не входят в правую часть системы алгебраических уравнений для определения опорных реакций (1.6), поэтому они примут вид:
[A] {X} = {0},
откуда следует, что {X} = {0}, так как для СОС det [A] ¹ 0.
3.Если нагрузку, приложенную к какому-либо диску составной системы заменить статически эквивалентной, то реакции и внутренние усилия в остальных дисках не изменятся.
4.Если изменить конфигурацию какого-либо диска составной системы, сохранив расположение опор и соединительных шарниров, то реакции и внутренние усилия в остальных дисках не изменятся.
5.Устранение в СОС любой связи, усилие в которой отлично от нуля, приводит к разрушению всей системы.
Напомним, что неподвижные СОС имеют минимальное число связей, необходимых для их образования, поэтому устранение любой такой связи превращает систему в механизм.
2.2.Внутренние усилия в рамах
2.2.1.Определения и порядок построения эпюр
Удобные для применения на практике определения внутренних усилий в рамах – впрочем, они будут справедливы для любых плоских стержневых систем – можно получить естественным обобщением соответствующих определений из сопромата.
Изгибающий момент M в поперечном сечении стержня рамы равен сумме моментов всех сил, взятых по одну сторону от сечения, которое делит раму на две части и вычисленных относительно точки, где сечение пересекает ось стержня.
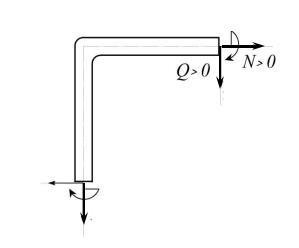
Поперечная сила Q в поперечном сечении стержня равна сумме проекций на нормаль n к оси стержня всех сил, взятых по одну сторону от сечения, которое делит раму на две части.
Продольная сила N в поперечном сечении стержня равна сумме проекций на касательную τ к оси стержня всех сил, взятых по одну сторону от сечения, которое делит раму на две части.
Правило знаков – в соответствии с рис. 2.1, где показан вырезанный двумя сечениями узел рамы.
M > 0
τ
|
|
N > 0 |
Q > 0 |
|
|
|
|
|
n
Q > 0
 M > 0 n
M > 0 n
N > 0
τ
Рис. 2.1
Для определения знаков внутренних усилий M, Q и N в каждом сечении вводят локальную систему координат с началом в центре тяжести сечения, орты которой аналогичны обычным ортам i, j декартовой системы координат. При этом орт τ направлен по внешней нормали (от тела) к плоскости поперечного сечения стержня, а орт n получается из орта τ путем его поворота по ходу часовой стрелки на угол 90°.
Как и в сопромате – см., например, [3] – внутренним усилиям N и Q соответствуют векторы N = Nτ и Q = Qn так, что N > 0 соответствуют растя-
жению стержней, Q > 0 – вращению рассматриваемого элемента по ходу часовой стрелки; M > 0 также направлен по ходу часовой стрелки.
Отметим, что необходимость введения такой локальной системы координат вызвана тем, что для вертикальных стержней рамы становится неопределенным понятие «верхние» и «нижние» волокна. Рассмотренная система отсчета вносит здесь полную ясность: на каждом рассеченном стержне рамы «верх» и «низ» будет определяться ортом n, направленным «вверх». Нетрудно убедиться, что при этом положительные моменты в сопромате и в строительной механике совпадают и соответствуют растянутым «нижним» волокнам.
Порядок построения эпюр. При построении эпюр внутренних усилий целесообразно придерживаться следующего порядка:
1) определяем опорные реакции;

2)делим раму на участки (i, j), границами которых являются естественные границы рамы, шарниры и угловые точки, точки приложения сосредоточенных сил, моментов и границы участков распределенной нагрузки;
3)в пределах каждого участка проводим сечение на расстоянии zi от его начала и вычисляем значения M, Q, N, рассматривая равновесие отсеченной части рамы;
4)строим эпюры, откладывая положительные значения Q и N на верхних (или левых для вертикальных стержней) волокнах, а M > 0 – на «нижних», то есть в направлении, противоположном нормали n.
5)проверяем правильность построения эпюр, рассматривая равновесие вырезанных узлов или других частей рамы и контролируя, как и для балок, соблюдение дифференциальных зависимостей Журавского на каждом из ее участков.
Примечания
1.Поскольку знаки эпюр Q и N привязаны не к локальной, а к глобальной системе координат, ставить знаки у эпюры M не имеет смысла – достаточно знать, что она построена на растянутых волокнах.
2.В строительной механике, в отличие от сопромата, эпюры принято строить именно
втакой последовательности: M, Q, N.
2.2.2. Построение эпюр в простых рамах
Рассмотрим пример построения эпюр внутренних усилий в соответствии с планом, приведенным в предыдущем параграфе.
Пример 2.1. Построить эпюры M,Q,N (рис. 2.2, а).
Решение. В этой задаче можно не определять опорные реакции, если рассматривать равновесие части рамы, не содержащей опору.
Делим раму на участки, проводим сечения в пределах каждого из них (рис. 2.2, б) и находим искомые усилия, рассматривая равновесие соответствующих частей рамы.
На первом участке (1-2) (рис. 2.2, в):
ΣMC = 0; qz1× z1/2 – M(z1) = 0; M(z1) = qz12/2 ;
Σt = 0; N (z1) = 0 ;
Σn = 0; qz1+Q(z1) = 0; Q(z1) = - qz1.
Для определения внутренних усилий на втором участке (2-3) рассмотрим равновесие части рамы выше соответствующего сечения (рис. 2.2, г):
ΣMC = 0; ql 2/2-M (z2) = 0; M (z2) = ql 2/2;
Σt = 0; ql +N(z2) = 0; N(z2) = - ql; Σn = 0; Q(z1) = 0 .
Переходя к последнему участку (3-4), будем для определенности считать, что на рис. 2.2, д z3 < l/2. Тогда:
ΣMC = 0; ql (l/2– z3) – M (z3)=0; M (z3) = ql (l/2 – z3);
Σt = 0; N(z3) = 0 ;
Σn = 0; - ql + Q(z3)= 0; Q(z3) = ql .
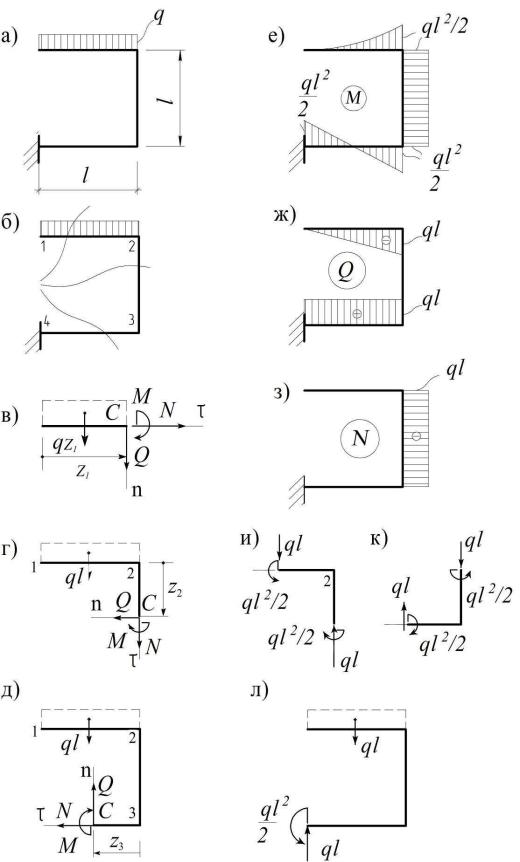
Рис.2.2
По найденным для каждого участка выражениям внутренних усилий строим соответствующие эпюры, показанные на рис. 2.2, е − 2.2, з.
Для проверки правильности построения эпюр можно рассмотреть равновесие вырезанных узлов рамы (рис. 2.2, и, к) и рамы в целом (рис. 2.2, л).
Контроль правильности построения эпюр на отдельных участках не отличается от соответствующей процедуры для балок.
Обратим внимание на следующие особенности построенных эпюр:
–при переходе через узел 2 с участка (1-2) на участок (2-3) эпюра M остается на внешних волокнах, то есть M(z1 = l) = M(z2 = 0);
–на участке (2-3) эпюра M = const , поскольку равнодействующая односторонних сил параллельна этому участку;
–в середине участка (3-4) эпюра M имеет нулевую точку, через которую
проходит равнодействующая распределенной нагрузки. ∙
Построение эпюр в рамах можно упростить, если воспользоваться стандартными эпюрами для консольной и двухопорной балок.
Например, в рассмотренном примере эпюры M и Q на участке (1-2) не будут, в соответствии с определением, отличаться от соответствующих эпюр в консольной балке, защемленной на правом конце – в точке 2.
Пример 2.2. Построить эпюры M, Q, N (рис. 2.3, а). Решение. Определяем опорные реакции:
ΣX = 0; |
XA = ql; |
ΣMA = 0; |
RB = ql/2; |
Σ MB = 0; YA = ql/2
и делим раму на участки (рис. 2.3, б).
Эпюры M, Q, N на стойке 1-2 рамы не отличаются от соответствующих эпюр в консоли, загруженной на свободном конце найденными реакциями (рис. 2.3, в). При этом вертикальная составляющая вызывает сжатие стойки, а горизонтальная – ее поперечный изгиб.
Для построения эпюр на участке 4-3 (именно так, а не 3-4) нужно рассмотреть стойку, загруженную распределенной нагрузкой и реакцией RB (рис.
2.3, г).
Переходим к построению эпюр на ригеле 2-3. Значения моментов на его концах известны – они находятся из условий равновесия узлов 2 и 3 и соответственно равны ql2 и ql2/2, а поскольку ригель не загружен, то эпюра на нем будет линейной (рис. 2.3, д).
Поперечную силу можно найти как тангенс угла наклона касательной к эпюре моментов: Q23 = ql/2, либо – по определению, как сумму проекций на вертикаль всех сил, взятых слева или справа от сечения, проведенного на этом участке (рис. 2.3, е).
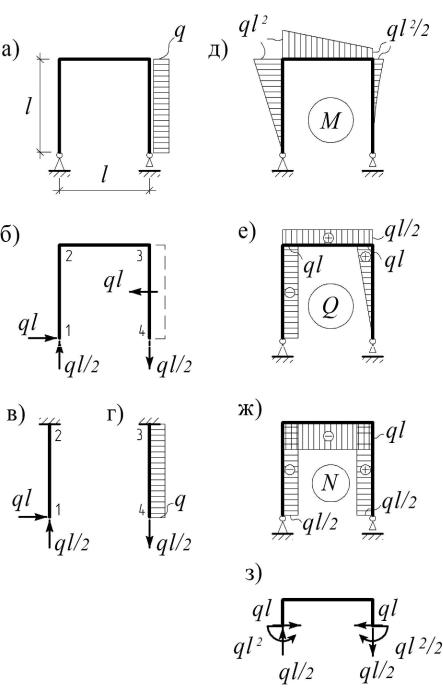
Аналогично находи м продольную силу N23 – как сумму проекций на горизонталь всех сил, взят ых по одну сторону от проведенн ого здесь сечения
(рис. 2.3, ж).
Рис.2.3
Для проверки правильности построения эпюр можно рассмотреть равно-
весие ригеля (рис. 2.3, з):
ΣX = ql – ql = 0; |
|
|
ΣY = ql/2 – |
ql/2=0; |
|
ΣM 2 = ql2 – |
ql2/2 – ( ql/2)·l = 0. |
∙ |
