10322

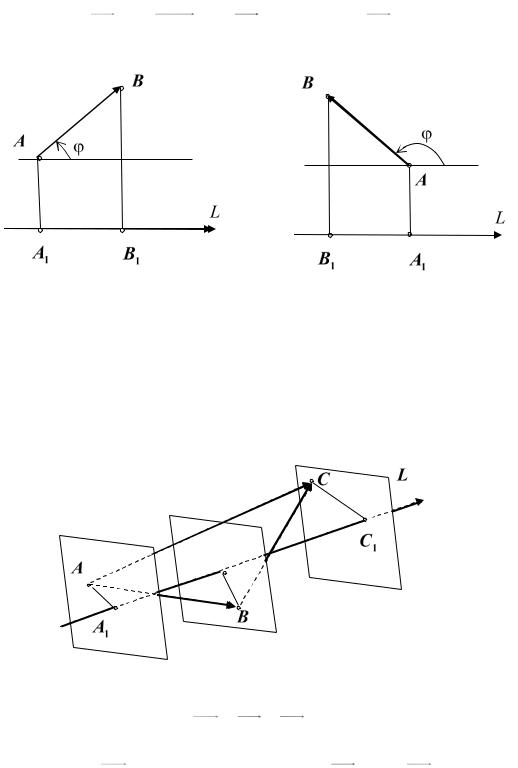
[Введите текст]

Доказательство. В случае, когда угол острый, утверждение очевидно. В случае тупого угла имеем (см. рис. 5.10)

ПрL AB | A1B1 | | AB | cos( ) | AB | cos

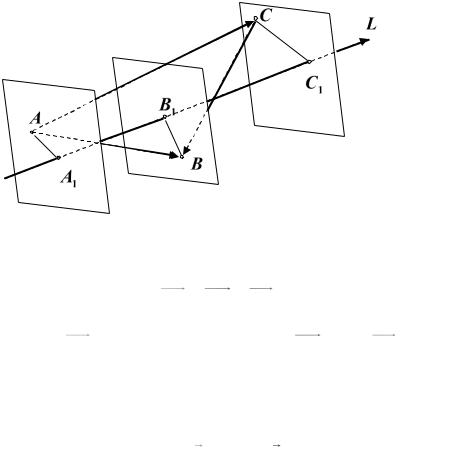
Рис. 5.11

AC AB BC

ПрL AC A1C1 A1B1 B1C1 ПрL AB ПрL BC

40

[Введите текст]

Рис. 5.12

AB AC CB

ПрL AB A1B1 A1C1 C1B1 ПрL AC ПрL CB .

Свойство 2. Если вектор умножается на число, то его проекция умножается на это же число

ПрL (ka) k ПрLa .

41

[Введите текст]

Лекция 6. Системы координат

6.1. Линейная комбинация векторов. Выше вектор был определен как геометрический объект – направленный отрезок. Перейдем теперь к эквивалентному его описанию в виде упорядоченного набора чисел. Для этого

bki ai .

i 1m

Теорема. Любой вектор a на плоскости единственным образом представим в виде линейной комбинации двух данных неколлинеарных векторов e1 и e2 этой плоскости.

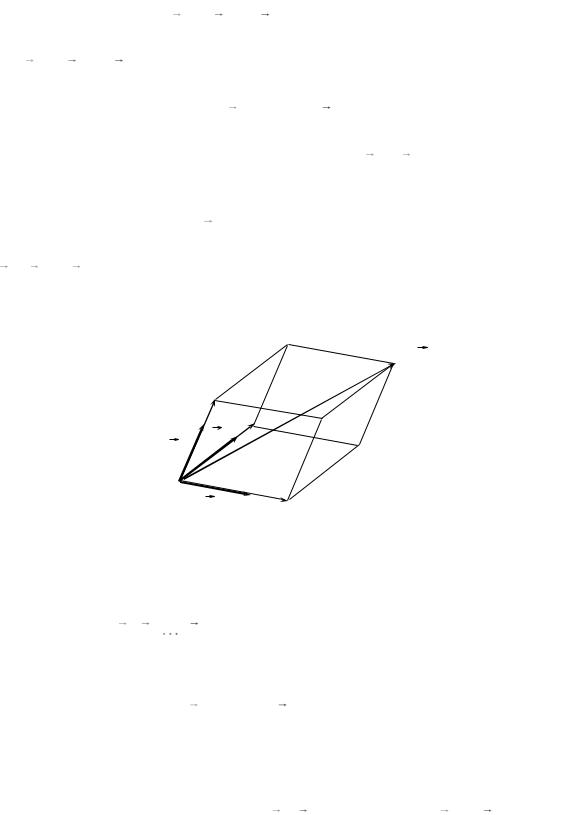
Доказательство. Поместим начала всех трех векторов в некоторую точку O (см. рис. 6.1). Из конца вектора a проведем прямые, параллельные векторам e1 и e2 , и обозначим через P и Q точки их пересечения с осями,

«проходящими» через векторы e1 и e2 , соответственно. По правилу сложения векторов имеем a OP OQ .

Рис. 6.1

Так как OP || e1 и OQ || e2 , то существуют такие числа a1 и a2 , что

OP a1e1 , OQ a2e2 .

42

[Введите текст]

Таким образом, получим a a1e1 a2e2 .

Покажем теперь, что такое представление единственно. Пусть это не так, т.е. a a1e1 a2e2 . Тогда после вычитания получим

(a1 a1 )e1 (a2 a2 )e2 0 .

Если хотя бы один из коэффициентов при векторах e1 и e2 , не равен нулю,

то отсюда будет следовать их коллинеарность, что противоречит предположению. Таким образом, указанное представление единственно.

Теорема. Любой вектор a в пространстве единственным образом представим в виде линейной комбинации трех данных некомпланарных векторов e1 , e2 и e3 .

Доказательство этой теоремы проводится аналогично доказательству предыдущей теоремы (см. рис.6.2)

a

R

Q

e3 e2 O

e1 P

Рис. 6.2

Введем свойство линейной зависимости векторов, обобщающее свойства коллинеарности и компланарности на случай произвольного числа векторов. Векторы a1, a1, , am называются линейно зависимыми, если

хотя бы один из них выражается в виде линейной комбинации остальных, то есть

i 1(i j )

В противном случае эти векторы называются линейно независимыми.

Из этих определений следует, что любые два коллинеарных вектора линейно зависимы, так как из условия a1 || a2 следует, что a2 ka1 , и что

любые три вектора на плоскости также линейно зависимы. Таким образом, приведенные выше теоремы можно переформулировать следующим образом: любой вектор на плоскости единственным образом представим в виде

43

[Введите текст]

линейной комбинации двух заданных линейно независимых векторов, а любой вектор в пространстве – в виде линейной комбинации трех заданных линейно независимых векторов.

Возможность такого представления любого вектора приводит к мысли определять вектор и его положение набором коэффициентов его линейной комбинации. Естественно возникают задачи определения положения вектора и его длины через этот набор коэффициентов. Эти задачи решаются с помощью операции скалярного умножения векторов.

6.2. Разложение вектора по базису. Координаты вектора. Базисом

{e1,e2 ,e3} называются взятые в определенном порядке линейно независимые

векторы. Термин базис (гр. basis – основание) отражает тот факт, что через эти векторы можно выразить любой вектор. Если базисные векторы взаимно перпендикулярны, то базис называется ортогональным, а если плюс к этому базисные векторы имеют единичную длину, то – ортонормирован-

ным.

Выражение данного вектора a в виде линейной комбинации базис-

ных векторов называется его разложением в данном базисе (или по ба-

зису):

a a1e1 a2e2 a3e3 .

Коэффициенты разложения {a1, a2 , a3} называются координатами вектора a в данном базисе, и записывается это так:

a a1,a2 ,a3 .

Таким образом, теперь вектор – это упорядоченная тройка чисел (на плоскости – пара чисел).

Операции над векторами в координатной форме

a b тогда и только тогда, когда ai bi , i ;

a b a1 b1, a2 b2 , a3 b3 ;

a a1, a2 , a3 ,

непосредственно следуют из определения. Например,

a b (a1e1 a2e2 a3e3 ) (b1e1 b2e2 b3e3 )

(a1 b1 )e1 (a2 b2 )e2 (a3 b3 )e3 ) {a1 b1 , a2 b2 , a3 b3}.

Условие коллинеарности двух векторов «в координатах» получается следующим образом: a || b тогда и только тогда, когда b a или bi ai i , т.е. их соответствующие координаты пропорциональны:

44

[Введите текст]

b1 b2 b3 . a1 a1 a3

6.3. Декартова система координат. Декартовой системой коорди-

нат называется совокупность фиксированной точки O (начала координат) и базиса векторов {e1,e2 ,e3}, исходящих из точки O . Оси, проходящие через

базисные векторы, называют соответственно осью абсцисс (ось Ox ), осью ординат (ось Oy ) и осью аппликат (ось Oz ). Плоскости, проходящие через

две какие-либо оси, называют координатными плоскостями.

Если базис ортогональный, то такая система координат называется де-

картовой прямоугольной системой координат. В ортонормированном ба-

зисе единичные базисные векторы принято обозначать через i , j , k . Оче-

видно, что «в координатах» эти векторы записываются следующим образом:

i {1, 0, 0}, j {0, 1, 0}, k {0, 0, 1} .

Радиус-вектором произвольной точки M называют вектор OM , а его координаты называют координатами этой точки. Если даны координаты то-

i

45

[Введите текст]

Рис. 6.3

Обозначим через , , углы между положительными направлени-

ями осей координат и вектором OM . Тогда проекции вектора OM выражаются следующим образом:

x PrOX OM | OM | cos , y PrOY OM | OM | cos , z PrOZ OM | OM | cos .

В частности, если вектор OM e единичной длины, то его координаты являются косинусами углов, которые этот вектор образует с осями координат, то есть

e{cos , cos , cos }.

Всвязи с этим координаты единичного вектора называют направляющими косинусами этого вектора.

Длина вектора может быть найдена по теореме Пифагора: из двух пря-

моугольных треугольников OMQ и OPQ следует, что

| OM | 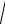x2 y2 z2 .

Таким образом, углы, которые вектор образует с осями координат, связаны следующим соотношением

e 2 cos2 cos2 cos2 1.

ная ось OP ) с началом в полюсе (см. рис.6.4)

46

[Введите текст]

Рис. 6.4

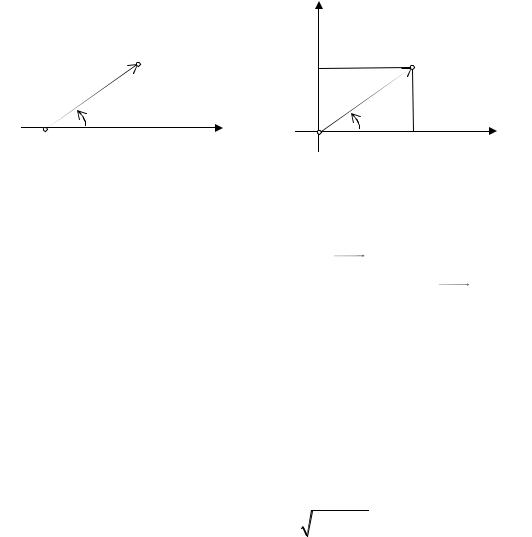
Тогда положение произвольной точки M на плоскости можно однозначно охарактеризовать двумя числами (r, ) , где r | OM | – расстояние этой

точки от полюса и – угол между полярной осью и вектором OM , отсчитываемый от полярной оси против часовой стрелки (см. рис. 6.4).

Выберем на плоскости две системы координат – декартову прямоугольную и полярную – так, что полюс находится в начале декартовой системы координат, а полярная ось направлена вдоль положительного направления оси абсцисс. Тогда любая точка M будет иметь декартовы координаты (x, y) и полярные (r, ) . Из рис. 6.4 непосредственно следуют соот-

ношения между полярными и декартовыми координатами (предполагается, что линейный масштаб одинаковый в обеих системах координат)

В полярной системе координат удобнее изображать кривую, расстояние точки которой от начала координат (полюса) определяется как функция направления (полярного угла). Например, так называемая «спираль Архимеда» определяется следующим образом: расстояние её точки до полюса пропорционально величине угла между полярной осью и радиусом-векто- ром этой точки. В соответствии с этим запишем уравнение этой кривой в полярной системе координат

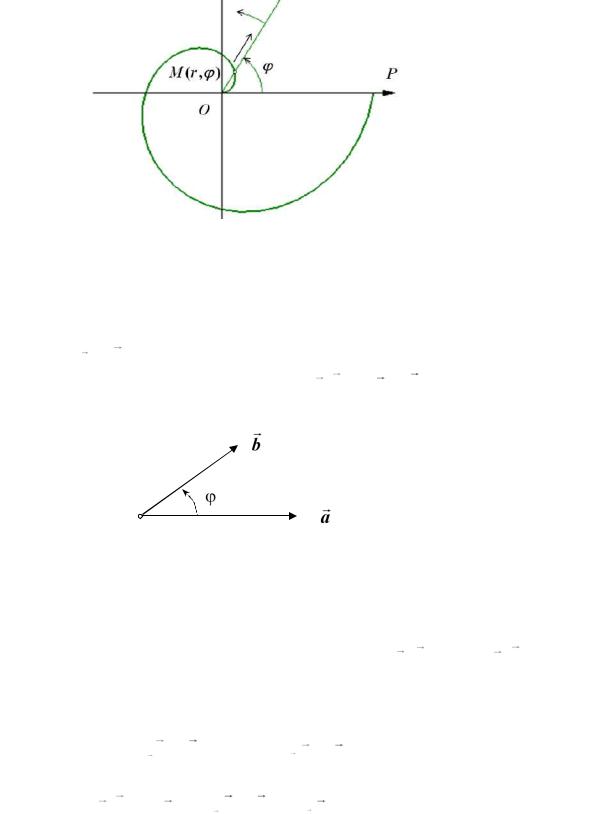
и построим ее график Спираль Архимеда можно рассматривать как траекторию движения точки, равномерно перемещающейся вдоль прямой, в то время как эта прямая равномерно вращается против часовой стрелки относительно полюса. На рис. 6.5 приведена часть этой спирали, соответствующая изменению полярного угла в пределах одного оборота.

47

[Введите текст]

Рис. 6.5

Лекция 7. Скалярное произведение

7.1. Скалярное произведение двух векторов. Скалярным произве-

дением векторов a и b называется число, равное произведению модулей этих векторов на косинус угла между ними a,b | a | | b | cos

Рис. 7.1

Под углом между двумя векторами будем понимать наименьший из двух углов между ними.

Обратим внимание на то, что результат этой операции может быть выражен через проекцию одного из векторов на другой. Действительно, так как

то (см. рис. 7.2) a,b | a | Пр a b | b | Пр b a

48

[Введите текст]

Рис. 7.2

С этой операцией в физике связано вычисление работы силы F при пере-

мещении материальной точки по направлению вектора S , когда угол между этими векторами равен . Тогда работа вычисляется по формуле

A | F | | S |cos F, S .

Операция скалярного произведения позволяет выразить проекцию вектора на вектор и угол между векторами следующим образом:

причем, если скалярное произведение векторов положительно, то угол между ними острый, а если отрицательно – тупой. В частности, скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны (ортогональны)

Из определения скалярного произведения следует коммутативность этой операции

a,b b,a ,

а из свойств проекций векторов вытекают следующие ее свойства:

ka,b a, kb k a,b , a,b c a,b a,c .

Докажем последнее из них

49