
10301
.pdf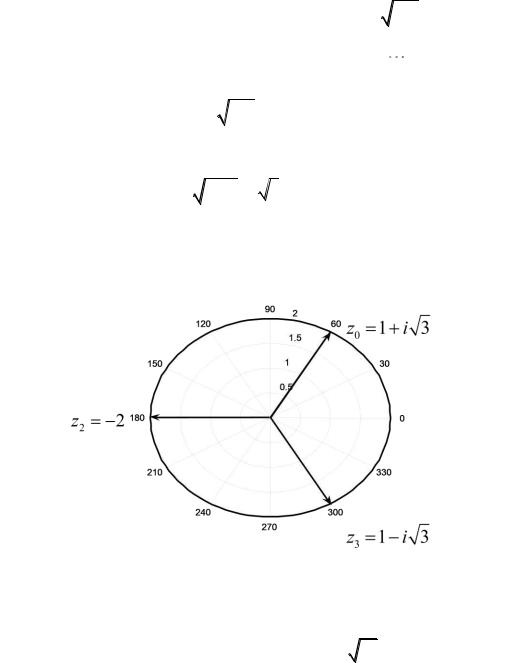
[Введите текст]
В этом легко убедиться, прибавив 2 к значению аргумента корня z k , что не меняет значений синуса и косинуса. Например,
|
|
|
2 |
|
|
|
2 |
|
cos n k . |
|
cos k |
cos |
|
|
( k) 2 |
cos |
|
|
(n k) |
||
n |
n |
|||||||||
|
n |
|
|
n |
|
|
|
Итак, мы получили n |
корней n -й степени из комплексного числа. Это – |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
комплексные |
числа, |
модули |
которых равны |
r n | a | , |
а |
аргументы |
||||||||||||||||||
определяются |
формулой |
|
|
2 |
k, |
k 0, 1, 2, |
, n 1. |
Особенно |
||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||
наглядна |
их геометрическая интерпретация: |
все корни расположены на |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
окружности, радиус которой |
r n |
| a | , и угол между соседними корнями |
||||||||||||||||||||||
равен |
2 |
. Например, уравнение z3 8 0 имеет три корня, расположенных |
||||||||||||||||||||||
n |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||||||||||
на окружности радиуса r 3 | 8 | 3 8 2 . |
Поскольку |
arg( 8) , то |
||||||||||||||||||||||
аргументы корней соответственно равны k |
|
|
|
2 |
k , k 0, 1, 2 . |
|||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
||
Рис. 32.1 |
|
В области действительных чисел символ |
( ) был «закреплён» за |
положительным корнем из положительного числа. Если расширить его применение для изображения корня из комплексного числа, то он потеряет однозначность. Например,
230
[Введите текст]
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 i , 3 8 |
|
|
|
. |
|||
|
|
||||||
|
|
|
1 |
i |
3 |
|
|
|
|
|
|
|
|
|
|
32.2.Квадратное уравнение.Рассмотрим квадратное уравнение
ax2 bx c 0 , коэффициенты которого действительные числа. Формально написанная формула для вычисления его корней
x |
b |
|
b2 4ac |
(32.1) |
|
|
|
||
1,2 |
|
2a |
|
|
|
|
|
||
во множестве действительных чисел не имеет смысла, если подкоренное
выражение b2 4ac отрицательно. Но теперь мы |
умеем |
находить |
квадратные корни из отрицательных чисел. Пусть d , |
(d 0) |
некоторое |
отрицательное число. Его тригонометрическая форма d d (cos i sin ) . Поэтому
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
d (cos( |
k) i sin( |
k)), |
k 0,1 |
|
d i d |
||||||
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
Следовательно, если дискриминант уравнения отрицателен, то

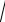 b2 4ac
b2 4ac 
 (4ac b2 ) i
(4ac b2 ) i 
 | b2 4ac | .
| b2 4ac | .
Формула вычисления корней квадратного уравнения принимает вид
|
|
|
|
|
|
|
|
|
|
b |
|
b2 4ac |
, |
|
b2 4ac 0 |
||
|
|
|
|
|
|
|
||
x1,2 |
|
|
2a |
|
|
|
||
|
|
|
|
|
|
|
|
|
b i | b2 4ac | |
|
|
||||||
|
|
, |
b2 4ac 0 |
|||||
|
|
|
|
|
2a |
|
||
|
|
|
|
|
|
|
|
|
В |
случае |
|
приведённого |
|
квадратного уравнения |
x2 px q 0 |
||||||||||||||||||
формулы имеют более компактный вид |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
p |
|
|
|
|
p |
|
2 |
q, ( |
p |
|
|
2 |
q 0 |
|
||||||||
|
|
|
|
|
( |
|
|
) |
|
|
) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
x1,2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(32.2) |
|
|
p |
|
|
|
|
|
p |
|
|
|
|
|
|
|
p |
|
|
|
||||||
|
|
|
i | ( |
) |
2 |
q | , |
( |
) |
2 |
q 0 |
|
|||||||||||||
|
|
2 |
|
2 |
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример.Решитьуравнение z3 8 0 . После разложения левой части уравнения на множители
231

[Введите текст]
(x 2)(x2 2x 4) 0
становится очевидным действительный корень уравнения x1 2 , а два комплексно сопряжённых корня находятся по формуле (32.2)
x2,3 1 
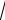 1 4 1
1 4 1 
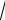 3 1 i
3 1 i
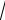 3 .
3 .
Геометрическая интерпретация корней данного уравнения дана на рис. 32.1.
32.3.Разложение многочлена на множители.Рассмотрим многочлен степени n
|
P (z) a zn a zn 1 |
a |
z a . |
|
||
|
n |
0 |
1 |
n 1 |
n |
|
Число |
z1 , обращающее |
этот многочлен в нуль |
( Pn (z1 ) 0 ), |
называют |
||
корнем |
уравнения Pn (z) 0 .На |
протяжении многих веков |
делались |
|||
попытки получить формулы для вычисления корней уравнений Pn (z) 0
степени n 3. В 1545 г. итальянский математик, философ и врач Д. Кардано (1501-1576) опубликовал формулы решения кубического уравнения. Возник спор о приоритете с другим итальянским математиком Николло Тарталья (1499-1557). Ученик Кардано Л.Феррари (1522-1565) нашёл способ решения уравнений четвёртой степенипутём сведения к решению кубического уравнения. Норвежский математик Нильс Абель (1802-1829) доказал, что алгебраические уравнения степени n 4 неразрешимы в радикалах. Это надо понимать в том смысле, что корни уравненияне выражаются через его коэффициенты ak с помощью конечного числаопераций сложения,
вычитания, умножения, деления и извлечения корня.
Важный результат о существовании корней алгебраического уравнения носит название основной теоремыалгебры. Эта теорема гласит,
что всякий многочлен Pn (z) степени n 1имеет по крайнейодин
комплексный корень.Эта теорема впервые (не вполне строго) была доказана французским учёным Ж. Даламбером (1717-1783).Строгое доказательство дал Карл Гаусс (1777-1855) в 1799 году. Основная теорема алгебры даёт возможность представления многочлена в виде произведения множителей, содержащих его корни
Pn (z) a0 (z z1 )(z z2 ) (z zn ) ,
откуда следует, что всякое алгебраическое уравнение имеет ровно n корней.
Некоторые из корней могут совпадать. Их называют кратнымив отличие от простых, т.е. неповторяющихся корней. Кратность корня – это
232
[Введите текст]
число его повторений в разложении многочлена на множители. С учётом кратности корней получим разложение многочлена
|
|
|
P (z) a (z z )r1 |
(z z |
2 |
)r2 |
(z z |
k |
)rk , |
||
|
|
|
n |
0 |
1 |
|
|
|
|
||
где z1, |
, zk – различные корни уравнения Pn (z) 0 , а r1, |
, rk – их кратности, |
|||||||||
причём |
r1 |
rk |
n . |
Указанные |
разложения |
|
справедливы для |
||||
многочленов, как с вещественными, так и с комплексными коэффициентами.
Отметим без доказательства, что если многочлен имеет вещественные
коэффициенты, то наряду с комплексным корнем |
z i многочлен |
обладает сопряжённым корнем z i , причём |
той же кратности. |
Объединяя в разложении многочлена такие пары, получаем
(z z)(z z ) (z i )(z i ) z2 2 z 2 2 z2 pz q .
Таким образом, многочлен с вещественными коэффициентами раскладывается на линейные множители с вещественными корнями и квадратичные множители с парой комплексно сопряжённых корней. Переменную в случае многочлена с вещественными коэффициентами будем обозначать буквой x . Итак, многочлен с вещественными коэффициентами имеет разложение
P (x) a (x x )r1 |
(x x )rr (x2 |
p x q )s1 |
(x2 p x q )sl , |
|||||
n |
0 |
1 |
|
k |
1 |
1 |
l |
l |
где r1 |
rk 2(s1 |
|
sl ) n . |
|
|
|
|
|
32.4. Разложение правильных дробей на простые дроби.Разложение многочлена на множители связано с задачей разложения правильной рациональной дроби
|
|
|
Qm (z) |
|
|
(32.3) |
|
|
|
|
Pn (z) |
|
|||
|
|
|
|
|
|||
на простые дроби следующих видов; |
|
|
|||||
|
A |
и |
|
Mx N |
( k |
1 и целое); |
|
|
|
|
|
||||
|
(x a)k |
|
(x2 px q)k |
||||
|
|
|
|
|
|
||
где A, M , N, a, p, q – |
действительные числа, а квадратный трёхчлен |
||||||
x2 px q не имеет действительных корней. Оказывается, что всякую
правильную рациональную дробь можно представить в виде суммы конечного числа простейших дробей. Этот алгебраический факт мы примем без доказательства.
233

[Введите текст]
Рациональная дробь называется правильной, если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе ( m n ). В противном случае ( m n ) рациональная дробь называется неправильной. Всякую неправильную рациональную дробьможно представить в виде суммы многочлена степени m n (целая часть) и правильной рациональной дроби, т.е.
|
Qm (x) |
Gm n |
(x) |
R(x) |
, |
|
Pn (x) |
Pn (x) |
|||
|
|
|
|
||
где степень многочлена R(x) меньше n . |
Для этого надо разделить |
||||
числитель на знаменатель по правилу деления многочленов. Это деление осуществим «уголком», причем делим до тех пор, пока показатель степени x в остатке не окажется меньше показателя степени x делителя.
Вид разложения дроби (32.3) определяется корнями многочлена Pn (x) . Если знаменатель Pn (x) имеет только действительные простые
корни, то
Qm (x) |
|
Qm (x) |
|
A1 |
|
A2 |
... |
An |
|
|
|
|
|
||||
Pn (x) |
|
an (x x1)(x x2 ) ... (x xn ) |
|
x x1 |
x x2 |
x xn |
||
где A1, A2 ,..., An –действительные числа, которые следует найти.
Если действительный корень xi знаменателя дроби имеет кратность ki ,то в разложении правильной дроби на простейшие этому корню
соответствует число дробей, равное |
ki : |
|
|
|
|||||
|
A1 |
|
A2 |
|
|
... |
Ak |
|
. |
|
x x |
(x x ) |
2 |
|
k |
||||
|
|
|
|
(x x ) i |
|||||
|
i |
|
|
i |
|
|
|
i |
|
Если знаменатель содержит |
множителем |
квадратный трехчлен |
|||||||
x2 px q , не имеющий действительных корней, то при разложении на простейшие дроби этому множителю соответствует дробь вида
Mx N
x2 px q .
Если знаменатель дроби имеет кратные комплексные корни,то множителю (x2 px q)l с комплексно сопряженными корнями соответствуют l дробей:
234
[Введите текст]
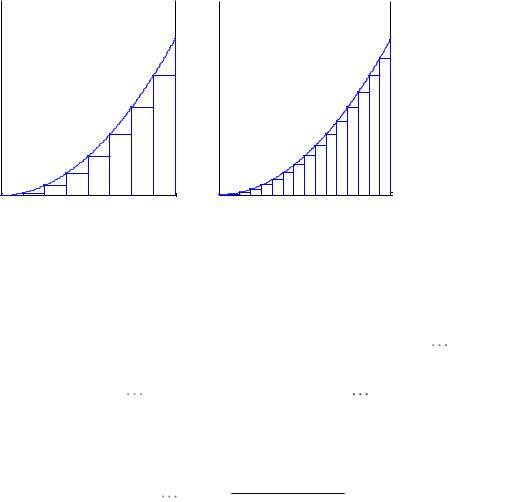
Площадь криволинейной трапеции. Пусть на отрезке [ a,b] задана
непрерывная положительная функция |
y f (x) . |
Фигуру, ограниченную |
|
осью Ox , прямыми x a , |
x b и |
графиком |
функции, называют |
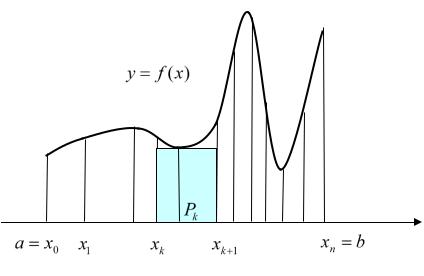
криволинейной трапецией. Для приближенного вычисления площади этой криволинейной трапеции разобьём промежуток [ a,b] произвольным
образом на n частей (см. рис. 33.2)
Рис. 33.2
В каждом интервале длиной xk xk xk 1 произвольно выберем точку pk
. Тогда площадь прямоугольника с основанием xk и высотой f ( pk ) будет равна f ( pk ) xk , а площадь под кривой приближенно равна сумме
n |
|
S Sn f ( pk ) xk . |
(33.1) |
k1
Сувеличением n точность этого приближения будет возрастать при условии, что длины всех отрезков xk будут уменьшаться. Назовем
площадью криволинейной трапеции предел последовательности Sn , если он существует и не зависит от способа разбиения и выбора точек.
33.2. Понятие определённого интеграла. Во всех приведенных выше задачах мы осуществляли следующую процедуру: брали некоторую функцию f (x) , разбивали интервал её определения на n частей, в каждой
части выбирали некоторую точку pk , составляли так называемую
интегральную сумму (33.1) и, наконец, находили предел последовательности этих сумм при n , когда длина наибольшего из отрезков дробления стремится к нулю. Получающийся при этом предел носит название определенного интеграла.
236
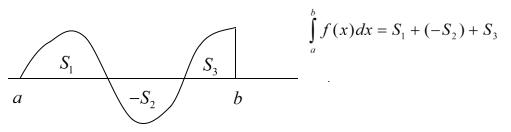
[Введите текст]
Определённым интегралом функции f (x) |
на промежутке [ a,b] |
|||||||
называется конечный предел интегральных сумм |
|
|
||||||
|
n |
|
b |
|
|
|
|
|
lim |
|
f ( p ) x |
|
f (x)dx, |
( max x |
|
0) , |
(33.2) |
n |
k k |
|
k |
k |
|
|
||
|
k 1 |
|
a |
|
|
|
|
|
если он существует и не зависит ни от способа разбиения промежутка [ a,b] , ни от выбора точек pk .
Ценность этого математического понятия состоит в том, что функцию f (x) можно «наполнять» разным содержанием: это может быть функция,
определяющая границу криволинейной трапеции, и тогда определенный интеграл выражает площадь трапеции, или это может быть функция, определяющая линейную плотность неоднородного стержня, и тогда определенный интеграл выражает массу стержня.
Для существования определенного интеграла функция f (x) должна
обладать некоторыми свойствами. Например, она должна быть ограниченной на [ a,b] . В противном случае интегральную сумму за счёт
выбора точек pk можно сделать как угодно большой. Оказывается, что
достаточным условием существования определённого интеграла служит непрерывность f (x) на [ a,b] .
Теорема.Если функция f (x) непрерывна на отрезке [ a,b] , то
определенный интеграл существует. Примем эту теорему без доказательства.
33.3. Основные свойства определённого интеграла. Обозначение определённого интеграла было введено Лейбницем. Знак интеграла – это стилизация первой буквы латинского слова summa.
Если подынтегральная функция отрицательна на всем промежутке интегрирования или на его части, то соответствующий множитель, входящий в интегральную сумму будет отрицательным. Если интеграл интерпретировать как площадь, то части кривой, расположенной под осью абсцисс будем приписывать отрицательную площадь (см. рис. 33.3).
Рис. 33.3
237
[Введите текст]
Если отказаться от допущения a b и принять a b , то в интегральной сумме все разности xk будут отрицательными. Поэтому
|
|
|
|
b |
f (x)dx a |
f (x)dx |
||||
|
|
|
|
a |
|
|
b |
|
|
|
В качестве определения полагаем также |
|
a |
f (x)dx 0 . |
|||||||
|
|
|
|
|
|
|
|
|
a |
|
Укажем основные свойства определённого интеграла, легко |
||||||||||
получаемые из его определения: |
|
|
|
|
||||||
|
b [ f (x) g(x)]dx b |
f (x)dx b g(x)dx |
||||||||
|
a |
|
|
|
a |
|
a |
|
|
|
|
b kf (x)dx k b |
f (x)dx, |
k const |
|
||||||
|
a |
|
a |
|
|
|
|
|
|
|
|
b |
f (x)dx c |
f (x)dx b g(x)dx, |
|
a c b |
|||||
|
a |
a |
|
|
|
c |
|
|
|
|
|
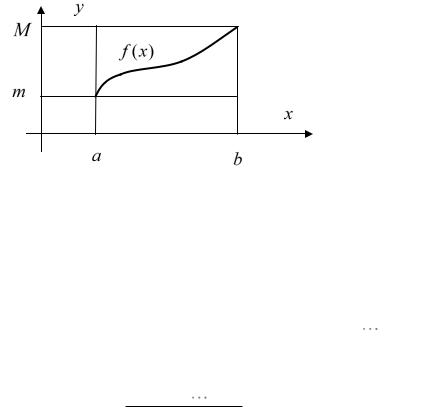
m(b a) b |
f (x)dx M (b a), |
|
m f (x) M |
||||||
|
|
a |
|
|
|
|
|
|
|
|
Последнее свойство проиллюстрируем рисунком (см. рис. 33.4).
Рис. 33.4
Иногда важно не столько найти точное значение интеграла, сколько получить его оценку. Указанное неравенство геометрически соответствует тому факту, что существует прямоугольник весь расположенный внутри криволинейной трапеции и прямоугольник – содержащий эту фигуру.
Среднее значение функции. Если даны n чисел a1, a2 , , an , то их
средним (средним арифметическим) называют число
a a1 a2 an .
ср |
n |
|
238

[Введите текст] |
|
Что следует понимать под средним значением функции |
f (x) на |
отрезке [ a,b] ? Существует, например, понятие средней |
плотности |
неоднородного тела (например, средняя плотность Земли примерно равна
5,5 ). |
Разделим |
отрезок |
[ a,b] |
|
|
на |
|
n |
равных |
частей |
||||||||
x1 x2 |
xn (b a) / n , |
возьмем в каждой части по точке |
Pk и |
|||||||||||||||
составим сумму |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
f (P ) f (P ) |
f (P ) |
|
1 |
|
n |
|
|
||||||||
|
|
|
|
|
f (Pk ) xk |
|
||||||||||||
|
|
|
1 |
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
n |
|
|
|
|
|
b a |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
||||
Перейдём в этой сумме к пределу |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
n |
|
|
|
|
|
1 |
b |
|
|
|
|
|||
|
|
lim |
|
f (P ) x |
|
|
|
|
f (x)dx f |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
b a |
n |
|
k |
k |
|
b a |
|
|
ср. |
|
||||
|
|
|
|
|
k 1 |
|
|
|
|
a |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким |
образом, под |
средним |
значением |
функции |
на отрезке |
[ a,b] |
||||||||||||
понимают отношение интеграла функции по этому отрезку к длине этого отрезка. Геометрический смысл среднего значения функции становится ясным, если его определение записать в виде
fср. (b a) b f (x)dx
a
Поскольку интеграл справа выражает площадь криволинейной трапеции, то левую часть равенства можно трактовать как площадь прямоугольника. Итак, среднее значение функции равно высоте прямоугольника, в основании которого лежит отрезок [ a,b] , равновеликого по площади
криволинейной трапеции (см. рис. 33.5).
Рис. 33.5
Особенно важно, что в силу непрерывности функции на отрезке [ a,b] найдётся такая точка P0 , что fср. f (P0 ) . Это даёт возможность выразить
239
