
10300
.pdf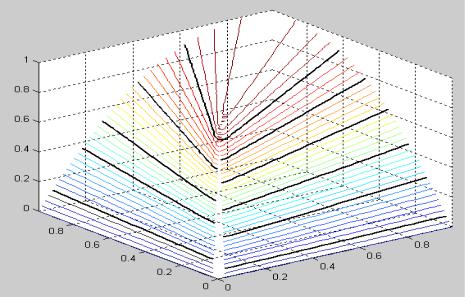
точке (x0 , y0 ) , соответствующая последовательность значений функции zn f (xn , yn ) сходится к A . Символически это записывается так
lim f (x, y) A .
x x0 y y0
В качестве примера приведем функцию z |
2xy |
, у которой не |
|
||
x2 y2 |
||
существует предела в начале координат. |
|
|
Рис.36.2
Действительно, пусть точка (x, y) движется к началу координат по прямой y kx, 0 k . Тогда
lim |
2xkx |
|
|
2k |
, |
x2 (kx)2 |
|
k 2 |
|||
x 0 |
1 |
|
|||
y 0 |
|
|
|
|
|
т.е. при стремлении аргументов к началу координат по разным направлениям получаются различные «предельные» значения функции (см.
рис. 36.2). |
|
|
Понятие предела даёт возможность |
определить |
непрерывность |
функции в данной точке. А именно, функция |
z f (x, y) |
непрерывна в |
точке (x0 , y0 ) , если
lim f (x, y) f (x0 , y0 ) .
x x0 y y0
Если подробно «прочесть» это равенство, то непрерывность означает, что
259
функция определена в данной точке и некоторой её окрестности;
существует предел функции в этой точке;
предел функции равен значению функции в этой точке.
При нарушении хотя бы одного из этих условий, говорят, что функция имеет разрыв в данной точке. Свойство непрерывности через приращения выражается так
lim[ f (x0 x, y0 y) f (x0 , y0 )] 0 ,
x 0y 0
т.е. непрерывность означает, что «малым» изменениям аргументов соответствуют «малые» изменения функции. Ясно, что эти понятия легко распространить на функции многихпеременных.
Если функция непрерывна в любой точке некоторой области, то говорят, что она непрерывна в этой области. Убедитесь, пользуясь
определением непрерывности, что функция z x2 y2 непрерывна в
любой точке плоскости.
36.3. Частные производные, производная по направлению. Для функции одной переменной производная в данной точке равна пределу отношения приращения функции к приращению аргумента, когда последнее стремится к нулю. В случае функции двух переменных приращения аргументов ( x, y) из данной точки M 0 (x0 , y0 ) в точку M (x0 x, y0 y) могут быть сделаны в любом направлении на плоскости. Это приводит к понятию производной функции по направлению, которая характеризует скорость изменения функции в выбранном направлении.
Начнем с простейшего случая, когда приращения происходят в направлении оси абсцисс, т.е. когда x 0, y 0 . В этом случае предел
lim |
f (x0 x, y0 ) f (x0 , y0 ) |
|
f (x0 , y0 ) f (x , y ) |
|
|
||||
x 0 |
x |
x |
x 0 0 |
|
|
||||
|
|
|
|
|
называется частной производной функции f (x, y) по переменной x в
точке M 0 (x0 , y0 ) . Аналогично можно определить частную производную по переменной y
lim |
f (x0 , y0 y) f (x0 , y0 ) |
|
f (x0 , y0 ) f (x , y ) . |
|
|
||||
y 0 |
y |
y |
y 0 0 |
|
|
||||
|
|
|
|
|
Из этих определений непосредственно следует, что для нахождения частной производной по данной переменной остальные переменные фиксируются и по обычным правилам дифференцирования отыскивается производная функции этой переменной. Например,
260
|
x |
|
z |
1 |
|
z |
|
x |
||
z |
|
, |
|
|
|
, |
|
|
. |
|
y |
x |
y |
y |
y2 |
||||||
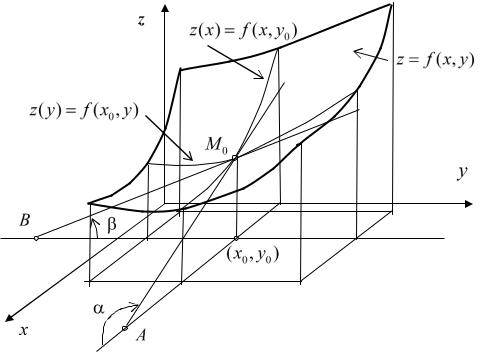
Выясним геометрический смыслчастных производных. Пусть в |
||||||||||
некоторой окрестности точки |
|
M 0 (x0 , y0 ) |
задана функция z f (x, y) , у |
|||||||
которой в этой точке существуют частные производные. Зафиксируем одну из переменных, например, переменную x .
Рис. 36.3
Тогда в плоскости x x0 (см. |
рис. |
36.3) мы получаем функцию одной |
||
переменной |
z( y) f (x0 , y) . |
График этой функции |
– это сечение |
|
поверхности |
z f (x, y) плоскостью |
x x0 . Значение её |
производной при |
|
y y0 равно значению частной производной по y функции f (x, y) в точке
M 0 (x0 , y0 )
dz( y) |
|
|
f (x0 , y) |
|
f (x0 , y0 ) |
tg , |
|
dy |
y |
y |
|||||
|
y y0 |
y y0 |
|
||||
|
|
|
|
|
где – угол между касательной BM 0 к кривой z( y) f (x0 , y) в точке M 0 и плоскостью xOy . Аналогичные рассуждения приводят к тому, что
f (x0 , y0 ) tg ,
y
261
где – угол между касательной AM 0 к кривой |
z(x) f (x, y0 ) |
в точке M 0 |
|
и плоскостью xOy . |
|
|
|
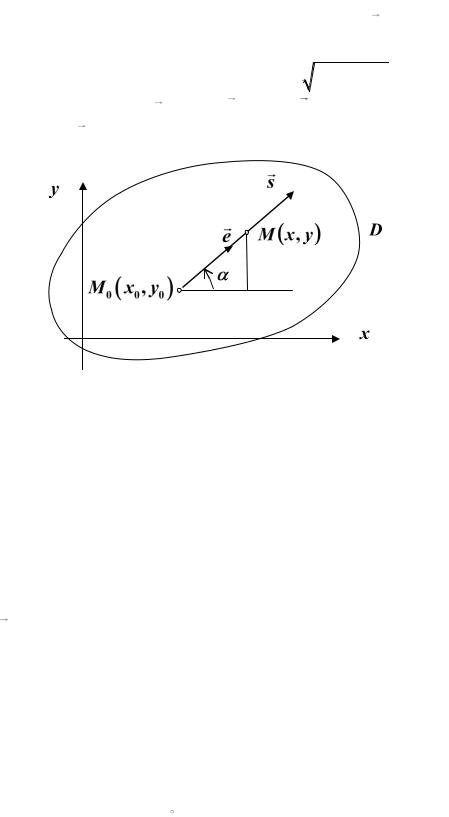
Рассмотрим теперь понятие производной по направлению. Пусть в |
|||
области D , в которой определена функция |
z f (x, y) , |
в |
некоторой |
внутренней точке M 0 (x0 , y0 ) задано направление вектором |
s (см. рис.1.5). |
||
Нас интересует, как быстро меняется значение функции при движении
|
|
|
|
точки M (x, y) вдоль этого направления. Пусть s |
x2 y2 расстояние |
||
между точками M 0 и |
M , а e cos i sin j |
– единичный вектор |
|
заданного направления |
s . |
|
|
∆
∆
∆
Рис. 1.5
Тогда координаты точки M (x, y) равны: x x0 x x0 s cos ,
y y0 y y0 s sin , а приращение функции в этом направлении
s z f (x0 s cos , y0 s sin ) f (x0 , y0 ) .
Если точка M стремится к точке M 0 , то s 0 . |
|
|
|
||||
|
Производной функции |
z f ( x, y) в точке |
M0 ( x0 , y0 ) в заданном |
||||
направлении s называется предел |
|
|
|
||||
lim |
s z |
lim |
f (x0 s cos , y0 |
s sin ) f (x0 , y0 ) |
|
f . |
(36.1) |
|
|
|
|||||
s 0 |
s |
s 0 |
s |
|
s |
|
|
В частности, частные производные |
z ; |
z |
это производные по |
|
|
|
|||
|
x |
y |
|
|
положительному направлению координатных осей. |
Найдём, например, |
|||
частную производную в точке M 0 (x0 , y0 ) |
положительном направлении |
|||
оси Ox . В этом случае угол 0 , y 0 , а |
s x и формула (36.1) |
|||
примет вид
262
lim |
x z |
lim |
f (x0 x, y0 ) f (x0 , y0 ) |
|
f |
|
x |
x |
x |
||||
x 0 |
x 0 |
|
Лекция 37. Производные сложных функций
37.1. Дифференцирование сложных функций. Будем предполагать,
что функция |
z f (x, y) имеет |
непрерывные частные производные в |
||||||||||
области D , а функции |
x(t) и |
y(t) |
имеют непрерывные производные в |
|||||||||
промежутке |
t . |
Тогда функция |
z f (x(t), y(t)) – сложная функция |
|||||||||
одной переменной |
t . |
Для производной |
dz |
этой функции справедлива |
||||||||
dt |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
следующая формула |
|
|
|
|
|
|
|
|||||
|
dz |
f |
dx |
f |
dy |
. |
|
(37.1) |
||||
|
|
|
|
|
|
|||||||
|
dt |
x dt |
y dt |
|
|
|
|
|
||||
Для доказательства рассмотрим приращение
z f (x, y) f (x0 , y0 ) f (x, y) f (x0 , y) f (x0 , y) f (x0 , y0 ) .
263

В первой из разностей изменяется только x , а во второй – только y , т.е.
каждая из этих разностей – это функция одной переменной. Применим кним формулу Лагранжа (формулу конечных приращений)
|
|
z fx ( , y)(x x0 ) f y (x0 , )( y y0 ) , |
|
где |
лежит в интервале между x и x0 , а – между y |
и y0 . К разностям |
|
x x0 |
и |
y y0 опять применим формулу Лагранжа |
|
|
|
x x0 x(t) x(t0 ) x (t1 )(t t0 ) x (t1 ) t |
|
|
|
y y0 y(t) y(t0 ) y (t2 )(t t0 ) y (t2 ) t , |
|
где t1 ,t2 |
расположены между t и t0 . Таким образом, |
|
|
|
|
z fx ( , y)x (t1) f y (x0 , ) y (t2 ) . |
|
|
|
t |
|
Переходя вэтом равенстве к пределу и замечая, что при |
t 0 имеем |
||
tt0 t1,t2 t0 x x0 , y y0 x0 , y0 ,
сучетом непрерывности всех, входящих в это равенство функций, получаем
dz |
fx (x0 |
, y0 )x (t0 ) f y (x0 , y0 ) y (t0 ) . |
||
|
|
|
||
|
||||
dt t |
|
|
||
|
|
0 |
|
|
В силу произвольности значения |
t0 приходим к формуле (37.1). |
|||
Заметим, что это |
естественное обобщение формулы производной |
|||
сложной функции одной переменной. В случае большего числа переменных, например, если z f (u(t),v(t), w(t)) , то
dz f du f dv f dw . dt u dt v dt w dt
37.2. Вычисление производной по направлению.Теперь мы можем получить формулу для вычисления производной по направлению. В самом деле, согласно определению (37.1) производная по направлению совпадает
с производной от сложной функцией |
z f (x( s), y( s)) , где |
|
x( s) x0 s cos , |
y( s) y0 s sin . Применяя формулу (37.1), |
|
получаем |
|
|
|
264 |
|

z |
|
f |
cos |
f |
sin . |
(37.2) |
|
l |
x |
y |
|||||
|
|
|
|
Обратим только внимание на тот факт, что в определении производной по направлению мы приближаемся к данной точке с одной стороны, т.е. имеем односторонний предел. Например, частная производная по отрицательному направлению оси абсцисс отличается знаком от частной производной по переменной x .
Аналогичным образом вводится понятие производной по направлению для функции трёх переменных u F (x, y, z)
|
u |
F cos |
F cos |
F cos , |
|
l |
x |
y |
z |
где |
e cos i cos j cos k – единичный вектор заданного направления |
|||
l , а |
, , – углы между осями координат и этим вектором. |
|||
Приведём без доказательства формулы для производной сложной функции z f (u,v) , u u(x, y), v v(x, y) . В итоге
z f (u(x, y),v(x, y)) (x, y)
будет функцией двух переменных и ее частные производные находятся по формулам
z |
|
f u |
|
f v |
, |
z |
|
f u |
|
f v . |
x |
|
u x |
|
v x |
|
y |
|
u y |
|
v y |
37.3. Дифференцирование неявных функций. Полученные нами правила дифференцирования сложных функций позволяют более просто, чем ранее, находить производные функций, заданных неявно. Пусть
уравнение |
|
F (x, y) 0 определяет |
|
y (x) как |
некоторую |
|||||||||
дифференцируемую функцию. Тогда имеем тождество F (x, (x)) 0 . |
||||||||||||||
Дифференцируем его по переменной |
x , рассматривая левую часть как |
|||||||||||||
сложную функцию одной переменной, где |
|
x x |
. |
|
||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
y (x) |
|
|
|
|
F dx |
F |
dy |
0 |
|
dy |
|
F |
F . |
(37.3) |
||||
|
|
|
|
|
|
|
||||||||
|
x dx |
y dx |
|
dx |
|
x |
y |
|
|
|||||
Пусть |
теперь |
уравнение |
F (x, y, z) 0 |
определяет |
z z(x, y) как |
|||||||||
некоторую функцию двух переменных, у которой существуют частные производные. Как их найти?
265

Продифференцируем тождество |
F (x, y, z(x, y)) 0 |
по переменной x , |
||||||||||||||
рассматривая |
его левую часть |
|
как |
сложную |
функцию F (u,v, w) , где |
|||||||||||
«промежуточные» функции имеют вид: u x , v y , z z(x, y) : |
||||||||||||||||
|
F dx |
|
|
F |
dy |
|
|
F z |
0 . |
|
||||||
|
|
|
|
|
|
|
|
|||||||||
|
x dx |
|
|
y dx |
z x |
|
|
|
|
|||||||
Поскольку x |
и y независимые переменные, то |
|
dy |
0 |
и, следовательно, |
|||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
z |
|
F |
F . |
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
x |
z |
|
|
|
|
|||
Аналогично, из равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
F dx |
|
|
F |
dy |
|
F z |
0 |
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
x dy |
|
|
y dy |
z y |
|
|
|
|
|||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z F |
F . |
|
|
|
|
||||||
|
|
|
|
|
y |
y |
z |
|
|
|
|
|||||
37.4. Градиент.При исследовании поведения функции двух переменных в данной точке естественно задаться вопросом: в каком направлении производная самая большая? Другими словами, в каком направлении у поверхности z f (x, y) в данной точке самый крутой склон?
Для ответа на этот вопрос введем следующий вектор
gradz fx i fy j ,
называемыйградиентом. Предполагаем, что этот вектор не нулевой. Тогда согласно (37.2) производная по направлению в данной точке равна скалярному произведению градиента в этой точке на единичный вектор заданного направления
|
z |
|
|
f |
cos |
f |
|
sin (gradz,e). |
||||
|
l |
x |
y |
|||||||||
|
|
|
|
|
|
|
|
|||||
Из равенства |
|
|
|
|
|
|
|
|
|
|||
|
|
z |
(gradz,e) |
|
gradz |
|
|
cos , |
||||
|
|
|
|
e |
||||||||
|
|
l |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
где – угол между векторами, видно, что направление наибольшего возрастания функции должно совпадать с направлением градиента функции в данной точке, т.к. наибольшее значение правой части этого равенства
266
достигается при 0 . Теперь становится понятным геометрический смысл градиента.
Градиент – это вектор, указывающий направление наибольшего возрастания функции в данной точке. Название происходит от латинского
gradior – идти вперёд. Термин и обозначение grad f ввёл Максвелл,
позаимствовав его из метеорологии. При первом появлении (1873г.) он намеревался дать название «скат» или «склон» скалярной функции f ,
используя слово slope, чтобы указать направление наиболее быстрого убывания функции f . Это свойство градиента применяется для численного
поиска экстремумов функции многих переменных.
В трёхмерном случае градиент определяется как вектор, координаты которого есть частные производные скалярной функции u F (x, y, z)
gradF Fx i Fy j Fz k .
Выясним геометрический смысл модуля градиента функции двух переменных. Пусть e – единичный вектор направления наибольшего возрастания функции в данной точке. Тогда производная по этому направлению равна
z |
|
|
|
|
|
|
|
(gradz,e) |
gradz |
|
z 2 |
z 2 . |
|||
|
|||||||
e |
|
|
x |
y |
|||
|
|
|
|
|
|||
отсюда следует, что модуль градиента – это «скорость» изменения функции в направлении наибольшего возрастания функции в данной точке. Как
характеризует величина |
этой «скорости» поверхность z f (x, y) в |
окрестностиданной точки? |
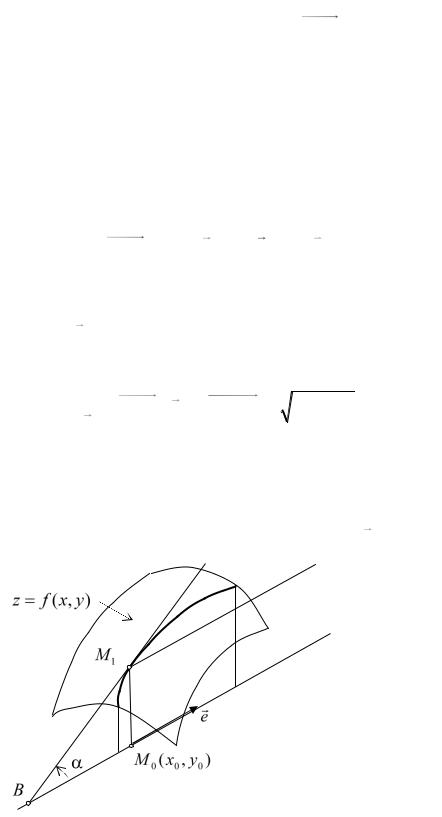
Рассмотрим сечение поверхности вертикальной |
плоскостью, проходящей через точку M (x0 , y0 ) и вектор e (см. рис. 37.1).
Рис. 37.1
267
Касательная |
BM1 к сечению поверхности в точке M1 (x0 , y0 , z0 ) составляет |
|||||||
с вектором |
e , а значит и с плоскостью |
xOy , |
угол , тангенс которого |
|||||
равен |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
tg |
|
gradz |
|
z |
2 z 2 . |
||
|
|
|||||||
|
|
e |
|
|
x |
y |
||
|
|
|
|
|
|
|
||
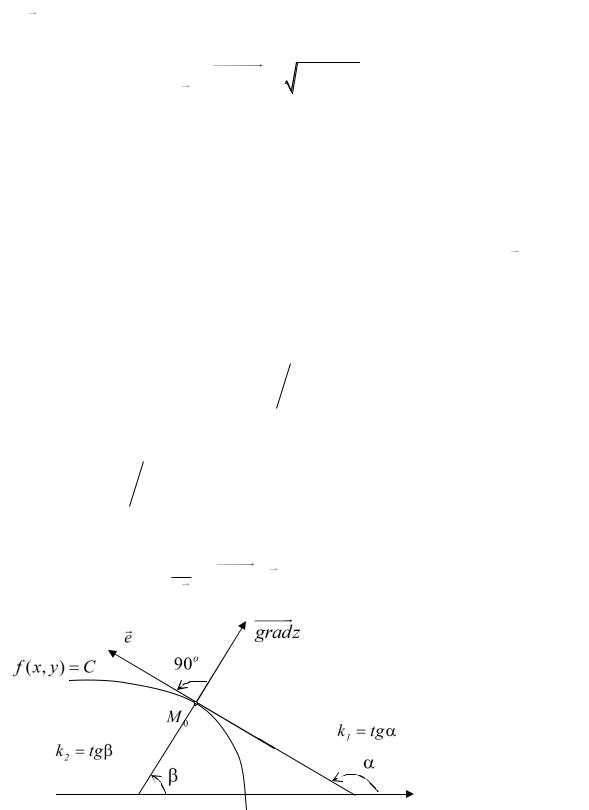
Эту величину называют крутизной подъёма поверхности в данной точке. Теперь убедимся в том, что в каждой точке градиент направлен по нормали к линии уровня f (x, y) C , проходящей через данную точку.
Пусть функция z f (x, y) имеет непрерывные частные производные, а её линия уровня, проходящая через точку M 0 (x0 , y0 ) , имеет касательную в этой
точке. Обозначим направление этой касательной единичным вектором e . Тогда производная по этому направлению в точке M 0 из интуитивных
соображений должна быть равна нулю. Убедимся в этом.
Угловой коэффициент k1 касательной к линии уровня f (x, y) C с учетом формулы (1.4) дифференцирования неявно заданной функции равен
|
|
|
|
|
k |
dy |
f |
|
f . |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
dx |
x |
|
y |
|
|
|
|
|
|
|
|
||||
С другой стороны, угловой коэффициент |
|
k2 прямой «в направлении |
||||||||
градиента» равен k |
2 |
|
f |
f |
. Так как |
k k |
|
1, то эти прямые взаимно |
||
|
|
y |
x |
|
|
|
1 |
2 |
|
|
перпендикулярны (см. рис. 37.2), т.е. производная в направлении касательной к линии уровня равна нулю
z (gradz,e) 0 .
e
Рис.37.2
Пример. Найти направление наибольшего возрастания функции
268
