
9809
.pdf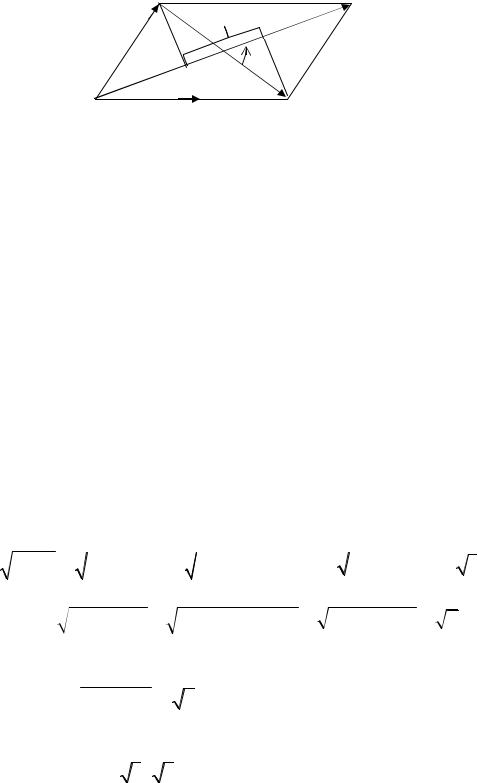
Введём декартову систему координат, взяв за начало точку A и вы-
брав базис {e1,e2} ≡ {0.5AB, AD} (см. рис.7.3). Пусть длины базисных векторов для определённости равны единице.
D C
?
e2
?
A |
e1 |
B |
Рис. 7.3
В этом базисе диагонали параллелограмма имеют разложение
d |
= DB = 2e |
- e |
, |
d |
2 |
= AC = 2e |
+ e . |
1 |
1 |
2 |
|
|
1 |
2 |
Искомые величины выражаются через скалярное произведение
cos(ÐBO C) = |
< d |
, d |
2 |
> |
Пр |
|
= |
< d , d |
|
> |
||
|
1 |
|
, |
d |
|
1 |
2 |
. |
||||
1 |
| d1 |
| |
× | d2 | |
d2 |
|
1 |
|
| d2 |
| |
|
||
|
|
|
|
|
|
|||||||
Вычисляем скалярное произведение, применяя более компактное по напи-
санию обозначение
d1 × d2 = (2e1 - e2 ) × (2e1 + e2 ) = 4e1 × e1 - e2 × e2 = 3.
Модули векторов вычисляем по формуле (7.1):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2e |
- e |
|
|
4e 2 |
- 4e e |
+ e 2 |
|
|
|
|
|||||
| d |
1 |
|= |
d |
× d |
= |
)2 |
= |
= 5 - 4cos60 = 3 |
|||||||||
|
|
1 |
1 |
|
1 |
2 |
|
|
1 |
1 |
2 |
2 |
|
|
|
|
|
| d2 |= 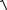
 (2e1 + e2 )2 =
(2e1 + e2 )2 = 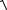
 4e12 + 4e1e2 + e22 =
4e12 + 4e1e2 + e22 = 
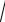 5 + 4cos60 =
5 + 4cos60 = 
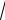 7 .
7 .
|
|
|
< d , d |
|
> |
|
3 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
Итак, |
= |
|
|
= |
|
|
»1.13 |
|||
Прd2 d1 |
| d2 | |
|
7 |
|||||||
|
|
|
|
|
|
|
||||
cos(ÐBO C) = |
|
|
3 |
|
|
» 0.65 ÐBO C » arccos 0.65 » 49 |
|
|
× |
|
|
||
1 |
|
3 |
7 |
1 |
||
|
|
|
|
|||
50
7.2. Скалярное произведение в прямоугольных координатах. Вы-
разим скалярное произведение через координаты его сомножителей. Пусть задана декартова прямоугольная система координат с ортонормированным
|
|
a = { ax , ay , az } |
|
|
b = { bx ,by ,bz } . Тогда, |
||
базисом { i , j, k } и два вектора |
и |
||||||
учитывая свойства скалярного произведения, получим |
|||||||
< a,b > = < a |
i + a |
j + a |
k , b i + b |
y |
j + b k > = |
||
x |
|
y |
z |
x |
|
z |
|
= axbx < i , i > + axby < i , j > + axbz < i , k > +
+ aybx < j ,i > + ayby < j , j > + aybz < j , k > +
+ azbx < k , i > + azby < k , j > + azbz < k , k > =
= axbx + ayby + azbz .
Итак, скалярное произведение равно сумме произведений одноимённых координат сомножителей:
< a,b > = axbx + ayby + azbz .
Теперь мы в состоянии выразить полученные выше формулы для модуля вектора, проекции вектора на вектор и угла между векторами в координатах данных векторов. А именно,
|
a |
|
= |
< a, a > |
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
a2 |
+ a2 + a2 |
, |
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
z |
|
|
|
|
|||
|
|
= |
< a,b |
> |
= |
axbx |
+ ayby + azbz |
|
|
||||||||||||||
Прb a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
bx2 + by2 + bz2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
| b | |
|
|
|
|
|
|
|
|
|
|||||||
cos ϕ = |
< a,b > |
= |
|
|
|
axbx |
+ ayby |
+ azbz |
|
. |
|||||||||||||
|
×| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
| a | |
b | |
|
|
|
ax2 + ay2 + az2 |
bx2 + by2 + bz2 |
|
|
||||||||||||||
В частности, условие ортогональности двух векторов выражается через их координаты следующим образом:
axbx + ayby + azb = 0 .
51

Продемонстрируем, как в декартовой системе координат решаются некоторые задачи.
7.3. Деление отрезка в заданном отношении: найти координаты точки
C(x, y, z), которая делит отрезок, соединяющий точки |
A(x1, y1, z1) |
и B(x2 , y2 , z2 ) |
||||||||||||||
(внутренним или внешним образом), в отношении |
λ (см. рис. 7.4). |
|
|
|||||||||||||
= |
> 0 |
|
|
|
|
= − |
|
|
|
|
||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
< 0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 7.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для её решения отметим, что |
векторы |
|
AC = {x − x1, y − y1, |
z − z1} и |
||||||||||||
CB = {x2 − x, |
y2 − y, z2 − z} коллинеарны, то есть AC = λ CB . Запишем это |
|||||||||||||||
векторное равенство в координатах: |
|
|
|
|
|
|
|
|
|
|
||||||
x − x1 = λ (x2 − x) , |
y − y1 = λ ( y2 − y) , |
z − z1 = λ (z2 − z) , |
|
|
||||||||||||
откуда найдем координаты точки |
C |
|
|
|
|
|
|
|
|
|
|
|||||
|
x = |
x1 + λ x2 |
, y = |
y1 + λy2 |
, z = |
z1 + λz2 |
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||||
|
|
|
1 + λ |
|
1 + λ |
|
|
|
1 + λ |
|
|
|
||||
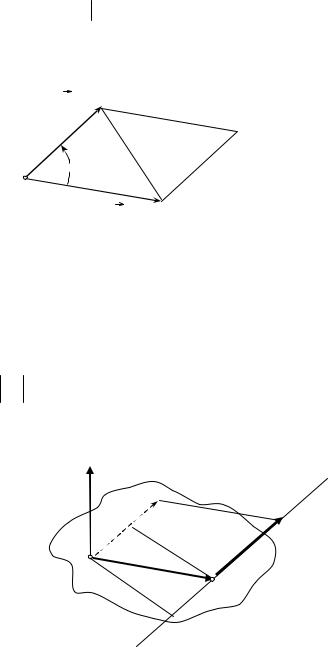
Покажем в заключение этого раздела, как векторная алгебра объясняет действие так называемого уголкового отражателя, представляющего собой комбинацию из трёх взаимно перпендикулярных зеркал. Многочисленные применения этого прибора связаны с его способностью менять направление света на строго противоположное независимо от того, с какого направления свет на него падает. Пусть луч света сначала попадает, например, на плоскость xOy и направляющий вектор этого луча a = {ax , ay , az }. Спрашивается, каков будет направляющий вектор a1 для
отражённого луча? Оба эти вектора одинаковой длины и расположены в плоскости, перпендикулярной к плоскости xOy . Очевидно, что у направляющего вектора отражённого луча третья проекция сменит знак, а первые две проекции останутся прежними, т.е. a1 = {ax , ay , −az } (см. рис. 7.5).
52
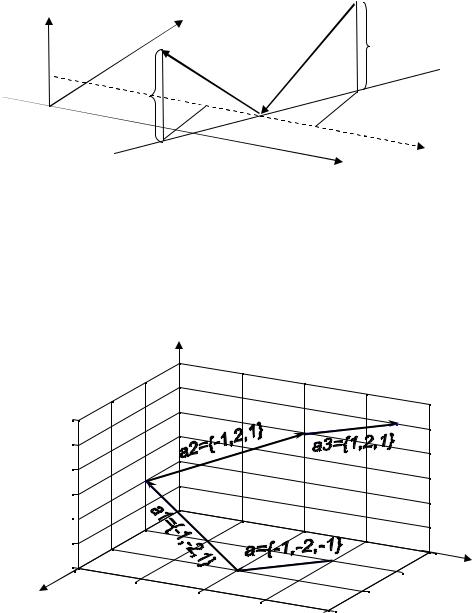
z |
y |
|
|
a |
az |
|
|
|
|
a1 |
|
|
−az |
|
O |
|
|
|
|
x |
|
Рис. 7.5 |
|
Таким образом, отразившись от трёх координатных плоскостей, луч света
будет иметь направление, противоположное |
первоначальному |
a3 = {−ax , −ay , −az } = −a . |
|
Следующий рисунок иллюстрирует «работу» уголкового отражателя на конкретном примере.
3
2.5
2
1.5
1 
0.5
0
0 |
|
|
0 |
|
1 |
1 |
|
2 |
2 |
|
|
|
3 |
3 |
|
4 |
|
|
|
Рис. 7.6
Уголковые отражатели применяются для точного измерения расстояний, обеспечения безопасности движения транспорта и в военном деле.
53
Лекция 8. Векторное и смешанное произведения векторов
8.1. Векторное произведение векторов. |
Векторным произведением |
векторов a и b называется вектор c = [a ´ b ] |
или просто c = a × b такой, |
что: |
|
·c a и c b
·упорядоченная тройка векторов {a,b , c} правоориентированная
· |
|
|
|
= |
|
|
|
× |
|
|
|
×sin j, где ϕ – угол между векторами. |
|
|
|
|
|
|
|||||||
|
c |
|
|
a |
|
|
b |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
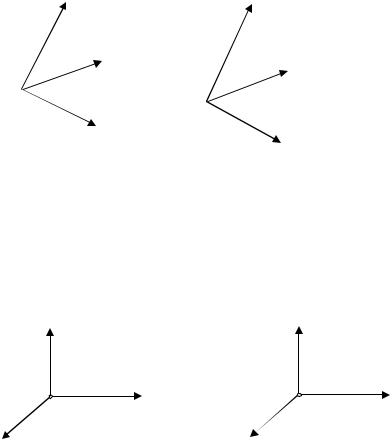
Упорядоченная тройка векторов называется правоориентированной или правой, если после приведения их к общему началу с конца третьего вектора c кратчайший поворот от первого вектора a ко второму вектору b виден происходящим против часовой стрелки. В противном случае – тройка называется левоориентированной или левой. При перестановке местами любых двух векторов или при замене одного из векторов на противоположный тройка меняет ориентацию.
c |
c |
b |
a |
a
b
Рис. 8.1
С этим расположением векторов a , b , c связаны правоориентированная и левоориентированная декартовы прямоугольные системы координат.
k |
k |
j |
i |
i |
j |
|
Рис. 8.2
54
Обратим внимание на то, что значение модуля векторного произве-
дения
|
= |
|
× |
|
× sin j |
c |
a |
b |
|||
|
|
|
|
|
|
равно площади параллелограмма, построенного на этих векторах
b
ϕ
a
Рис. 8.3
В механике с помощью этой операции вычисляется момент силы. Пусть, например, O – одна неподвижная точка некоторого тела, к другой точке A которого приложена сила F . Момент этой силы относительно неподвижной точки выражается векторным произведением M = OA × F , а его модуль равен M =| F | ×| OA | sin j =| F |d – « произведению силы | F |
на плечо d =| OA |sin j».
M |
|
* = + |
|
|
|
|
|
|
Мест |
d |
+ |
|
|
|
|
|
d |
|
|
Рис. 8.4
Рассмотрим основные свойства операции векторного произведения. Во-первых, эта операция позволяет выяснить коллинеарны или нет два заданных вектора. А именно, векторы a и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулю
a || b a × b = 0 .
55
Действительно, это следует из равенства |
|a ´ b |=| a | × | b | sin 0 = 0 . |
||
Что произойдет, если в векторном произведении |
c = a × b |
переста- |
|
вить местами сомножители, т.е. что собой представляет вектор |
d = b × a ? |
||
Очевидно, что вектор d перпендикулярен векторам |
a и b , его модуль |
||
равен модулю вектора c , но тройка {b , a, c} |
стала левой, а, значит, тройка |
||
{b , a, -c} будет правой. Таким образом, d = −c или [a × b ] = −[b × a ] .
c
b
O
d |
a |
|
Рис. 8.5
Умножение одного из сомножителей векторного произведения на число приводит к умножению результата на это число, т.е.
[ ka ´ b ] = [ a ´ kb ] = k [a ´ b ] .
В выражениях, содержащих векторное произведение и сложение, скобки «раскрываются» так же, как и при обычном умножении и сложе-
нии, т.е.
[(a + b) × c] = [a × c] + [b × c] .
Как найти векторное произведение, если его сомножители заданы своими координатами? Пусть векторы a и b в ортонормированном бази-
се векторов {i , j , k }, образующих правую тройку, |
имеют следующее раз- |
||||||
ложение: |
|
|
|
|
|
|
|
a = a |
i + a |
y |
j + a |
k , |
b = b i + b |
y |
j + b k . |
x |
|
z |
|
x |
z |
||
Вначале приведем таблицу векторного умножения базисных векторов, где в левом столбце находится первый сомножитель, в верхней строке – второй, а на пересечении строки и столбца соответствующее произведение.
56

Таблица 1. Вычисление векторного произведения координатных ортов в
правоориентированной системе координат
× |
i |
|
j |
k |
|
|
|
|
|
i |
0 |
k |
|
- j |
|
|
|
|
|
j |
- k |
0 |
|
i |
|
|
|
|
|
k |
j |
- i |
|
0 |
|
|
|
|
|
Теперь, используя эту таблицу и приведенные выше правила раскрытия скобок, получим:
[a × b ] = [ ( ax i + a y j + az k ) × ( bx i + by j + bz k )] =
= axbx [i × i ] + aybx [ j × i ] + azbx [k × i ] + +axby [i × j ] + ayby [ j × j ] + azby [k × j ] +
+axbz [i × k ] + aybz [ j × k ] + azbz [k × k ] =
=i (aybz − azby ) − j (axbz − azbx ) + k (axby − aybx ) =
|
ay az |
− |
|
|
a |
x |
a |
z |
|
|
ax ay |
||||
|
|
||||||||||||||
= i |
b |
|
b |
j |
|
b |
b |
|
+ k |
b |
b |
|
|||
|
y |
|
|
|
x |
z |
|
|
y |
||||||
|
|
z |
|
|
|
|
|
|
|
x |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы запомнить, как вычисляются координаты векторного произведения, заметим, что
|
|
|
|
|
|
|
|
|
|
||||
|
|
i |
j |
k |
|
|
[a |
× b] = |
ax |
ay |
az |
|
, |
|
|
bx |
by |
bz |
|
|
|
|
|
|
|
|
|
где в правой части равенства стоит символический определитель, раскрывая который по элементам первой строки, получим приведенное выше выражение векторного произведения через координаты сомножителей. Такое представление векторного произведения позволяет обнаружить те его свойства, о которых говорилось выше. Например, при смене порядка сомножителей в определителе поменяются местами две строки, что приводит
57

к смене знака определителя, а, значит, к смене знака векторного произведения. Любознательный читатель может таким образом проверить справедливость и других свойств векторного произведения.
Полученное выражение векторного произведения через координаты сомножителей дает возможность вычислить площадь треугольника по координатам его вершин
b
a
A( x1 , y1 , z1 )
C ( x3 , y3 , z3 )
B( x2 , y2 , z2 )
Рис. 8.6
Образуя какую-нибудь пару векторов, например,
a = |
|
= { x |
|
− x , y |
|
− y , z |
|
− z |
} = { a , a |
, a |
} и |
|
AB |
2 |
2 |
2 |
|||||||||
|
|
|
1 |
1 |
1 |
1 |
2 |
3 |
|
|||
b = AC = { x3 − x1, y3 − y1, z3 − z1} = { b1 , b2 , b3}
найдём
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
1 |
|
|
i |
j |
|
||
|
|
|
|
|
|
|
|||||
S = |
|
| a |
× b |= |
|
| |
|
a a a |
| . |
|||
2 |
2 |
||||||||||
|
|
|
|
|
1 |
2 |
3 |
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
b1 |
b2 |
b3 |
|
|
8.2. Смешанным произведением векторов |
a , b , c называется чис- |
||||||||||
ло, равное |
|
< a × b,c > , |
|
|
|
|
|
|
|||
|
|
|
|
|
|
(8.1) |
|||||
т.е. сначала находится вектор d = a × b , а затем он умножается скалярно на вектор c . Поэтому смешанное произведение иногда называют векторноскалярным произведением векторов. Отметим, что смешанное произведение выражается через скалярное и векторное произведения и не является какой-то «новой» операцией над векторами. Как мы сейчас увидим, знак смешанного произведения говорит о взаимной ориентации данных трех векторов (правую или левую тройку они образуют), а его модуль дает объем параллелепипеда, построенного на этих векторах.
58

Действительно, рассмотрим рисунки с правой и левой тройками векторов
|
|
c |
d |
c |
|
θ |
|
b |
|
|
a |
|
|
θ |
|
|
b |
|
a |
d |
|
|
Рис. 8.7 |
Из рисунков видно, что в случае правой тройки {a,b , c} вектор d = a × b образует с вектором c острый угол θ , а в случае левой тройки – этот угол тупой. С учетом того, что
< a ´b,c > = | d | ×| c | cos θ ,
мы получим, что в первом случае знак смешанного произведения будет положительным, а во втором – отрицательным. Таким образом, знак смешанного произведения «говорит» о взаимной ориентации тройки векторов
впространстве.
Ачто означает равенство нулю смешанного произведения? Очевидно, что это будет тогда и только тогда, когда cos θ = 0 , т.е. θ = π / 2 и, сле-
довательно, вектор c должен лежать в плоскости векторов a и b . Итак, обращение в нуль смешанного произведения эквивалентно компланарности данной тройки векторов.
- *
Рис. 8.8
59
