
9809
.pdf
Интегрируем по частям u = ln x, du = 1 dx, dv = dx, v = x x
|
|
e |
1 |
|
|
|
S = x ln x |
|
1e − ∫ x |
d x = e − x |
|
1e = e − e + 1 = 1. |
|
|
|
|||||
|
|
|||||
|
x |
|
||||
1 |
|
|
||||
|
|
|
|
|||
Формула Ньютона – Лейбница даёт возможность установить правило замены переменной в определённом интеграле. Пусть требуется вычис-
лить интеграл
b
∫ f (x)d x ,
a
где функция f ( x) непрерывна в промежутке |
[ a, b ] . Пусть функция |
x = ϕ (t ) удовлетворяет следующим условиям: 1) |
ϕ (t) непрерывна вместе |
|
′ |
сложная |
со своей производной ϕ (t) в некотором промежутке [α,β]; 2) |
||
функция f (ϕ(t )) |
должна быть определена в этом промежутке (для этого |
|
достаточно, например, потребовать, чтобы ϕ (t) была монотонна); |
3) кон- |
|
цам промежутка |
[α,β] соответствуют концы промежутка [ a, b ] , т.е. |
|
ϕ (α) = a, ϕ (β) = b или ϕ (α) = b , ϕ (β) = a (см. рис. 34.2). |
|
|
x |
x |
|
b |
x = ϕ(t) |
b |
|
|
|
|
|
|
|
a |
x = ϕ(t) |
a |
|
|
|
|
|
t |
t |
|
β |
β |
|
α |
α |
Рис. 34.2
При этих условиях имеют место формулы
b |
β |
′ |
|
∫ f (x)d x = ∫ |
|||
f (ϕ(t))ϕ (t)d t |
|||
a |
α |
(34.1) |
|
|
α |
||
b |
′ |
||
∫ f (x)d x = ∫ |
|||
f (ϕ(t))ϕ (t)d t |
|||
a |
β |
|
|
|
240 |
|
|

Приведём доказательство первой из них. Пусть F ( x) – одна из пер-
вообразных |
функции f ( x) . |
|
Тогда |
F (ϕ(t)) |
– первообразная функции |
|
′ |
Действительно, |
|
|
|
|
|
f (ϕ(t))ϕ (t) . |
|
|
|
|
|
|
|
′ |
|
′ |
′ |
′ |
|
|
Ft (ϕ(t)) |
= Fϕ (ϕ(t))ϕ |
(t) = f (ϕ(t))ϕ (t) . |
|||
Применяя формулу Ньютона – |
Лейбница |
к обоим интегралам в первом из |
||||
|
|
|
|
|
|
b |
равенств (34.1), получим, с одной стороны, |
∫ f (x)d x = F (b) − F (a) , а с |
|||||
a
другой
β
∫ f (ϕ(t))ϕ′(t)d t = F (ϕ(t) βα = F (ϕ(β)) − F (ϕ(α)) = F (b) − F (a) .
α
Аналогично можно убедиться в справедливости второго равенства в (34.1). Следует заметить, что, в отличие от замены переменной в неопределённом интеграле, здесь нет необходимости возвращаться к «старой» переменной. Если вычислены правые из интегралов (34.1), то, тем самым, вычислены и левые интегралы. Излишне упоминать, что не каждая подстановка ведёт к упрощению: какую замену переменной следует применять –
это может подсказать лишь опыт.
Пример. Вычислить площадь, ограниченную эллипсом, заданным
уравнением |
x2 |
+ |
y2 |
= 1. Ясно, что достаточно вычислить площадь четвёр- |
|||||
a2 |
b2 |
||||||||
|
|
|
|
|
|
|
|||
той части фигуры. Задача приводит к вычислению интеграла |
|||||||||
|
|
|
|
a |
|
|
|
||
|
|
|
|
2 |
|
|
|||
|
|
|
|
Sэл = 4b∫ |
1 − |
x |
|
dx . |
|
|
|
|
|
2 |
|||||
|
|
|
|
0 |
|
a |
|||
|
|
|
|
|
|
|
|
||
Опыт вычисления неопределённых интегралов «подсказывает» замену пе-
ременной |
x(t) = a sin t . Она удовлетворяет перечисленным выше услови- |
||||||
ям: |
|
|
′ |
|
|
||
∙ |
x(t ) |
|
|
|
|||
и x (t) = acost непрерывны в промежутке [0, π / 2] |
|||||||
∙ |
x(0) = 0, |
x(π / 2) = a |
|
|
|||
∙ |
|
|
|
= |
|
= cos t определена в [0, π / 2] . |
|
функция |
|
1 − x2 (t) a2 |
1 − sin2 t |
||||
Произведя эту замену, получаем |
|
|
|||||
|
|
|
|
π 2 |
π 2 |
||
|
|
|
Sэл = 4b ∫ cos2t dt = 2ab ∫ (1 + cos 2t )dt = πab . |
||||
|
|
|
0 |
|
0 |
||
|
|
|
|
|
|
241 |
|
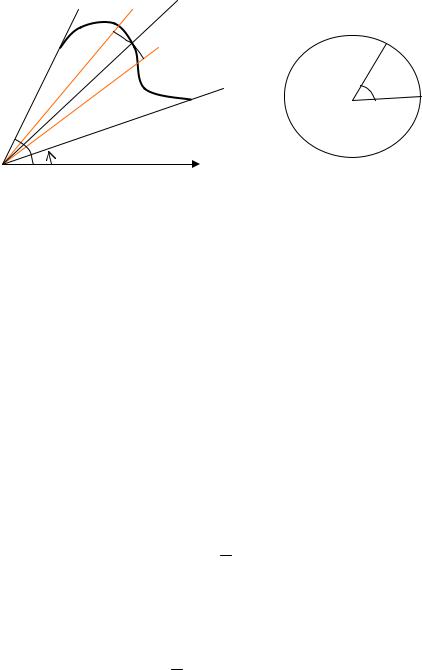
Переходя к пределу при n → ∞ , причём так, что длина максимального из
частичных отрезков λ = max(Δϕk ) стремится к нулю, получаем
k
S = lim |
1 |
n |
ρ2 (ξ |
|
)Δϕ |
|
= |
1 |
β |
ρ2 (ϕ)dϕ . |
|
∑ |
k |
k |
|
∫ |
|||||
n→∞ 2 |
|
|
2 |
|
||||||
λ→0 |
|
k =1 |
|
|
|
|
|
|
α |
|
Замечание. Если начало координат находится внутри области, ограниченной замкнутой кривой ρ = ρ(ϕ) , 0 ≤ ϕ ≤ 2π , то площадь вычисляется по формуле
2π
S = 1 ∫ ρ2 (ϕ )dϕ .
2 0
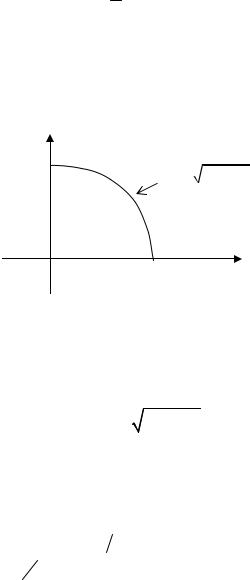
Пример 1. Вычислить площадь круга, граница которого задана уравнением x2 + y2 = R2 . Ясно, что достаточно найти площадь четверти круга
(см. рис. 34.4).
y
y = 
 R2 − x2
R2 − x2
x
O R
Рис. 34.4
Если вычисления проводить в декартовой системе координат, то получается «плохой» интеграл
|
|
|
|
|
|
1 |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
Skp = ∫ R2 − x2 dx . |
|||||||||
|
|
|
|
|
4 |
||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Перейдём к полярным координатам по формулам: |
x = ρ cos ϕ, y = ρ sin ϕ . |
||||||||||||||
Уравнение четвёртой части окружности |
|
x2 + y2 = R2 в полярных коорди- |
|||||||||||||
натах примет вид |
ρ = R, |
0 ≤ ϕ ≤ π 2 . Поэтому |
|
||||||||||||
|
|
|
|
π |
|
|
|
|
|
|
π |
|
πR2 |
|
|
1 |
1 |
2 |
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
|
||||||||
|
|
Skp = |
|
∫ |
R2dϕ = |
|
R2ϕ |
|
= |
|
Skp = πR2. |
||||
|
4 |
2 |
2 |
0 |
4 |
||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Вычислить площадь, ограниченную одним витком спирали Архимеда и полярной осью. Спираль Архимеда можно рассматривать как траекторию точки, равномерно движущуюся по лучу, исходящему из
243
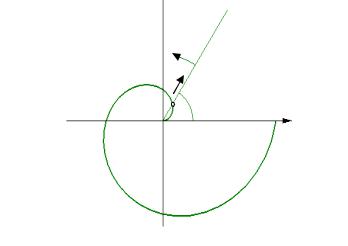
полюса, в то время как этот луч равномерно вращается вокруг полюса. В полярной системе координат её уравнение имеет вид ρ = aϕ , a > 0, a = const . Один виток спирали получается при повороте луча на угол ϕ = 2π . Искомая площадь выражается интегралом
|
1 |
2 π |
|
a |
2 |
× j |
3 |
|
2 π |
||
|
|
|
|||||||||
S = |
∫ |
(aj)2 dj = |
|
|
|
= |
4 |
a2p3. |
|||
|
|
|
|
|
|||||||
2 |
0 |
2 |
3 |
|
3 |
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
ϕ P
O
Рис. 34.5
34.3. Вычисление площади фигуры, ограниченной кривыми, за-
данными параметрически. Интерпретируя определённый интеграл площадью криволинейной трапеции, мы предполагали, что кривая y = f ( x) задана в явном виде. А как быть, если границы фигуры заданы параметрическими уравнениями? Заметим, что задание кривой в явном виде – это частный случай её параметрического задания, когда в качестве параметра избрана переменная x :
x = x |
|
|
a ≤ x ≤ b . |
y = |
f (x) |
В выборе параметра мы располагаем большой свободой. Например, при вычислении площади эллипса мы представляли его уравнение в параметрическом виде следующим образом:
x = a sin t |
0 ≤ t ≤ |
π |
. |
|
2 |
||
y = b cos t |
|
|
Таким образом, замена переменной в определённом интеграле – это, по сути, переход к другой параметризации кривой y = f ( x) . Поэтому, если часть кривой, площадь под которой нас интересует, задана параметрически, то применяется формула
244
|
b |
β |
′ |
|
|
x = x(t) |
α ≤ t ≤ β . |
|
|
|
|
|
|||
|
S = ∫ y(x)dx = ∫ y(t)x (t)dt , где |
|
|||||
|
a |
α |
|
|
|
y = y(t) |
|
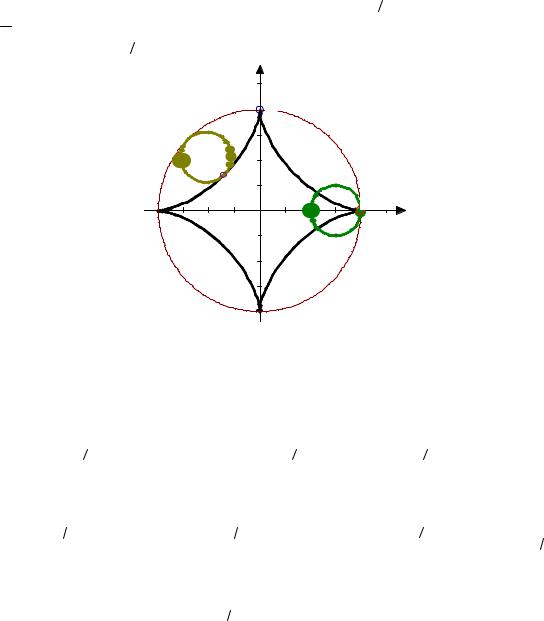
Пример 3. Найти площадь, ограниченную астроидой, заданной урав- |
|||||||
нениями |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
= a cos t |
|
|
|||
|
|
x |
≤ t ≤ 2π |
|
|||
|
|
|
|
|
0 |
|
|
|
|
y = a sin3 t |
|
|
|||
|
|
|
|
|
|
|
|
Астроиду можно рассматривать как траекторию фиксированной точки ок- |
|||||||
ружности, катящейся изнутри |
по окружности радиуса |
a и имеющей ра- |
|||||
диус |
a / 4 (см. рис. 34.6). В силу симметрии фигуры, вычисляем четвёртую |
||||||
часть её площади |
|
|
|
|
|
|
|
1 |
a |
0 |
|
|
|
π 2 |
|
S = ∫ y(x)dx = |
∫ a sin3 t ×3acos2t(-sin t)dt = 3a2 ∫ sin2 t cos2t × sin2 tdt |
||||||
4 |
0 |
π 2 |
|
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
Y |
|
|
|
|
|
|
|
t=pi/2 |
|
|
|
|
|
|
|
|
t=0 X |
|
|
|
|
0 |
|
|
a |
|
|
|
|
Рис. 34.6 |
|
|
||
После применения формул понижения степени тригонометрических функ- |
|||||||
ций получим |
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
π 2 |
|
|
|
3 |
|
|
π 2 |
|
|
|
|
|
3 |
|
π 2 |
|
|
|
|
|
|||||||
S = |
a2 |
∫ sin 2 2t (1 − cos2t)dt = |
a2 |
∫ sin 2 2t dt − |
a2 |
∫ sin2 2t cos 2tdt = |
|||||||||||||||||||||||||||
4 |
|
|
|
8 |
|||||||||||||||||||||||||||||
|
|
8 |
|
0 |
|
|
|
|
|
|
8 |
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3 |
|
π 2 |
|
|
|
3 |
|
|
|
π 2 |
|
|
3 |
|
|
|
|
π 2 |
3 |
|
|
π0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= |
a2 ∫ |
(1 - cos4t)dt - |
a2 ∫ sin2 2t d sin 2t = |
|
|
a2t |
|
- |
a2 sin 4t |
|
2 - |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
16 |
0 |
16 |
|
|
|
0 |
|
|
|
|
|
16 |
|
|
|
|
0 |
|
64 |
|
|
|
|
||||||||||
|
|
|
|
|
|
− |
1 |
a2 sin3 2t |
|
π 2 = |
3 |
a2π |
S = |
3 |
πa2 . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
16 |
|
|
|
|
0 |
32 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
245 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Лекция 35. Другие приложения определённого интеграла
В предыдущей лекции мы применили определенный интеграл к вычислению площадей фигур. Здесь будут рассмотрены другие его приложения.
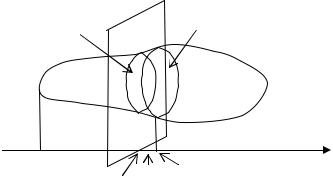
35.1. Вычисление объёма тела с известной площадью поперечного сечения. Пусть некоторое тело в направлении оси абсцисс находится в пределах отрезка [ a, b ] . Как обычно, разбиваем этот отрезок на n частей и через точки деления проводим плоскости P , перпендикулярные оси Ox . Эти плоскости рассекут тело на «дольки». На рисунке изображена одна из них.
S ( xk ) |
P |
S ( xk +1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
xk |
xk +1 |
|
b |
|
||
xk |
|
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 35.1 |
|
|
|
|
|
|
|
|
Предполагается, что для каждого значения |
x |
известна площадь |
сечения |
|||||
S (x) . Предполагается, что это непрерывная |
функция. Объём |
каждой |
||||||
«дольки» можно приближённо вычислить как объём цилиндра с площадью основания S (xk ) и высотой xk . Поэтому объём тела приближённо равен сумме объёмов таких цилиндров
n
V ≈ ∑ S (xk ) xk
k =1
Точное значение объёма получим, увеличивая число n точек деления от-
резка [ a, b ] . При этом длина наибольшего из отрезков λ = max( xk ) долж- |
|||
|
|
|
k |
на стремиться к нулю, т.е. находим предел интегральной суммы |
|||
n |
|
|
b |
V = lim ∑S (xk ) xk = ∫ S (x)d x |
|||
n→∞ |
|
|
|
λ→0 k =1 |
|
|
a |
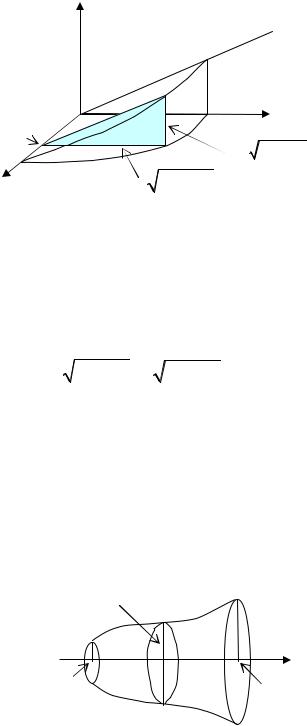
Пример. Найти объём части кругового цилиндра x2 + y2 = R2 , отсе- |
|||
чённого плоскостями x = 0, z = 0, |
z = |
h |
y . |
|
|||
|
|
R |
|
|
246 |
|
|
z
|
|
|
|
|
|
|
z = |
h |
y |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
R |
||
|
|
|
h |
|
|
|
|
|||
|
|
R |
y |
|||||||
x |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
− x2 |
||||||
|
|
|
|
|||||||
R |
|
|
|
|
|
R2 |
||||
|
|
|
|
|||||||
|
|
|
|
R |
|
|
|
|
||
x |
|
R2 − x2 |
|
|
|
|
||||
|
Рис. 35.2 |
|
|
|
|
|||||
Через фиксированную точку |
x [0, R] проводим плоскость, перпендику- |
|||||||||
лярно оси Ox . Сечение тела представляет собой прямоугольный треугольник, площадь которого
S (x) = |
1 |
|
|
|
|
h |
|
|
|
= |
h |
(R2 − x2 ) . |
|
|
||||||
|
|
R2 − x2 |
|
|
||||||||||||||||
|
|
|
|
R2 − x2 |
|
|
||||||||||||||
|
R |
|
|
|
||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
2R |
|
|
|
|
|
||||
Отсюда объём |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
h |
R |
|
|
h |
|
|
|
x |
3 |
|
R |
1 |
|
|||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
V = ∫ S ( x)d x = |
|
∫(R2 − x2 )d x = |
(R2 x − |
|
) |
= |
hR2 . |
|||||||||||||
|
2R |
2R |
|
|
3 |
|||||||||||||||
0 |
|
|
0 |
|
|
|
|
3 |
|
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
35.2. Вычисление объёмов тел вращения. Пусть криволинейная трапеция, ограниченная кривой y = f ( x) , a ≤ x ≤ b , вращается относительно оси Ox . Найдём объём полученного тела вращения.
y = f (x)
a |
b |
Рис. 35.3
Поскольку нам известна площадь поперечного сечения тела для каждого
значения x , а именно (сечение – круг): |
S (x) = π f 2 (x) , то |
b |
b |
Vx = ∫ S (x)d x = π∫ f 2 (x)d x . |
|
a |
a |
247
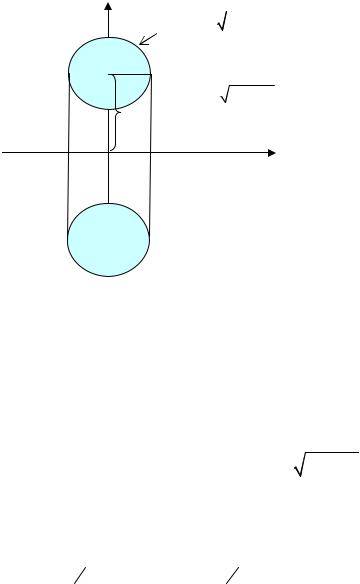
Пример. Найти объём тора («баранки»). Тор можно получить, вра-
щая относительно оси Ox окружность |
x2 + ( y − a)2 = r2 |
||||
y |
|
= a + |
|
|
|
y |
2 |
r2 |
− x2 |
|
|
|
|
|
|
|
|
 y1 = a −
y1 = a − 
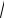 r 2 − x2
r 2 − x2
a
r
x
Рис. 35.4
Интересующий нас объём равен разности объёмов, полученных при вра-
щении кривых y1 и |
y2 . Поскольку фигура симметричная, то можно вы- |
||||||||||||
числять половину объёма |
|
|
|
|
|
|
|||||||
|
1 |
r |
|
|
r |
|
r |
|
|
|
|
||
|
V = π∫( y22 − y12 )d x = π∫( y1 + y2 )( y1 − y2 )d x = 4aπ∫ r2 − x2 d x |
|
|||||||||||
2 |
|
||||||||||||
0 |
|
|
0 |
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
Применим подстановку |
x = r sin t . Тогда будем иметь |
|
|
|
|
||||||||
|
|
|
|
|
|
|
π |
|
π |
|
|
|
|
|
|
|
1 |
|
2 |
|
2 |
|
|
|
|
||
|
|
|
V = 4aπ r 2 ∫ cos2 (t)d t = 2aπ r 2 ∫ (1 + cos 2t)dt = |
|
|||||||||
|
|
2 |
|
||||||||||
|
|
|
0 |
|
0 |
|
|
|
|
||||
|
|
|
|
|
π |
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
= 2aπr2 (t + |
sin 2t) |
2 = aπ2r2 . |
V |
= 2π2ar 2. |
|
||||||
|
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
тора |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
35.3. Несобственные интегралы. Вводя определённый интеграл как |
|||||||||||||
предел интегральных сумм |
|
|
|
|
|
|
|||||||
|
|
|
|
b |
|
|
|
n |
|
|
|
|
|
|
|
|
|
∫ f (x)dx = lim |
∑ f (xk ) xk , |
λ = max xk , |
(35.1) |
||||||
|
|
|
|
|
|
|
n→∞ |
k=1 |
k |
|
|
|
|
|
|
|
|
a |
|
|
λ→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
248 |
|
|
|
|
|

мы предполагали, что подынтегральная функция f ( x) непрерывна, а промежуток интегрирования [ a, b ] конечной длины. Распространим понятие определённого интеграла на более широкий класс функций. Пусть функция имеет в промежутке [ a, b ] разрывы первого рода. В этом случае под интегралом функции следует понимать сумму интегралов
b c b
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx ,
a a c
взятых по отдельным интервалам, в которых функция остаётся непрерыв-
ной (см. рис. 35.5).
f (x)
a |
c |
b |
Рис. 35.5
При этом и геометрическое значение интеграла как площади остаётся в силе.
Иначе обстоит дело, когда функция имеет разрыв второго рода в какой либо точке внутри интервала интегрирования или на одном из его концов. Начнём с примера. Так, формально написанный интеграл
1 |
dx |
|
|
||
∫ |
|
(35.2) |
|||
|
|
|
|||
x |
|||||
0 |
|
|
|
||
не существует в обычном смысле, т.к. подынтегральная функция «уходит в бесконечность» на левом конце промежутка интегрирования (см. рис. 35.6). Попытаемся придать вполне определённый смысл интегралу (35.2), а значит, и понятию площади соответствующей бесконечной фигуры. Проведем прямую x = ε и рассмотрим полученную криволинейную трапецию. Ее площадь равна интегралу
1 |
|
dx |
|||
∫ |
|
|
x |
|
|
ε |
|
|
|
. |
|
|
|
|
|
||
249 |
|
|
|
|
|
