
9803
.pdf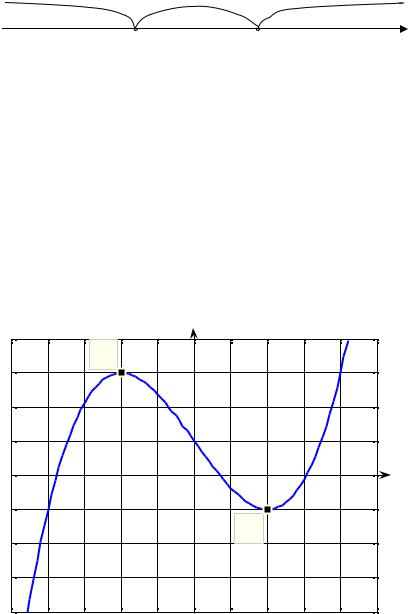
x = −1 |
и x =1. Отметим на следующей схеме знаки производной в соот- |
||||||||||
ветствующих интервалах |
|
|
|
|
|
|
|
|
|||
|
|
|
+ |
|
|
_ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
−1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
Рис. 22.7 |
|
|
|
|
||
Отсюда видно, что в интервале (−∞,−1) функция возрастает, а в интервале |
|||||||||||
(−1,1) – |
убывает, |
следовательно, |
при |
x = −1 |
функция имеет максимум |
||||||
ymax = f (−1) = 3 . Соответственно |
ymin = f (1) = −1. |
На основе этих данных |
|||||||||
можно построить график этой функции (см. рис. 22.8). «Попутно» мы вы- |
|||||||||||
яснили, что уравнение |
x3 − 3x +1 = 0 |
имеет три корня |
|
|
|||||||
|
|
|
−2 < x1 < −1, 0 < x2 < 1, 1 < x3 < 2 . |
|
|||||||
|
4 |
|
|
X: -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y: 3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X: 1 |
|
|
|
|
|
-2 |
|
|
|
|
|
Y: -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
|
|
|
|
-4 |
-2 |
-1.5 |
-1 |
-0.5 |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
|
-2.5 |
||||||||||
|
|
|
|
|
Рис. 22.8 |
|
|
|
|
||
|
|
|
|
|
160 |
|
|
|
|
|
|
Лекция 23. Исследование функций и построение их графиков (продолжение)
23.1. Выпуклость. Понятие выпуклости – одно из важнейших понятий всей математики. Мы ограничимся применением этого понятия к исследованию выпуклости графика функции. Обратимся к рисунку.
y
f2 ( x)
f1 ( x)
x
Рис. 23.1
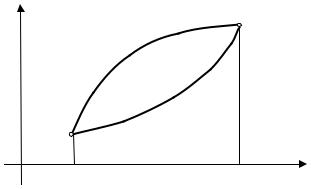
Пусть в промежутке (a,b) заданы две дифференцируемые функции. Их графики – это непрерывные кривые, имеющие в каждой точке касательную. Обе функции возрастают в этом промежутке. Но график одной из них обращен «горбом» вниз, а у другой – в противоположную сторону. Это свойство кривой называют выпуклостью. Как описать это свойство в математических терминах?
В математике есть понятие выпуклой функции, применяемое к более широкому классу функций, чем класс дифференцируемых функций. Мы определим это понятие именно для дифференцируемых функций. Будем называть функцию y = f (x) выпуклой (вниз) в промежутке (a,b) , если её график лежит выше касательной в любой точке из этого промежутка
(см. рис. 23.2).
В противном случае функцию называют вогнутой (выпуклой вверх). Аналитически это свойство выразится следующим неравенством
f (x) ³ f ′(x0 )(x - x0 ) + f (x0 ) = Y (x) ,
правая часть которого представляет собой значение ординаты касательной.
161

y |
R(x) = y −Y (x) |
|
y = f (x) |
||
|
|
|
a |
x 0 |
x |
|
b |
|
x |
|
|
|
|
|
||||
|
|
|
Рис. 23.2 |
|
|
|
|
|
Условие выпуклости. Если функция |
y = f (x) |
имеет в промежутке |
||||||
(a,b) положительную вторую |
производную |
f |
′′ |
> 0 , то кривая |
||||
(x) |
||||||||
y = f (x) выпукла (вниз). |
|
|
|
|
|
|
||
Для обоснования возьмём любую точку |
x (a,b) |
и рассмотрим |
||||||
функцию |
|
R(x) = f (x) − f (x0 ) − f |
′ |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(x0 )(x − x0 ) . |
|
|||||
Применим формулу Лагранжа к разности f (x) − f (x0 ) и получим |
||||||||
|
R(x) = f ′(ξ)(x − x0 ) − f ′(x0 )(x − x0 ) = ( f ′(ξ) − f ′(x0 ))(x − x0 ) , |
|||||||
где точка |
ξ расположена между точками x |
и |
x0 . К разности производ- |
|||||
ных f ′(ξ) − f ′(x0 ) опять применим формулу Лагранжа |
|
|
||||||
|
|
R(x) = f ′′(η)(ξ − x0 )(x − x0 ) , |
|
|
||||
причём точка η |
находится между точками |
ξ |
и |
x0 . Покажем, что произ- |
||||
ведение |
(ξ − x0 )(x − x0 ) положительно независимо от расположения точки |
|||||||
x по отношению к точке x0 . Пусть сначала точка |
x |
располагается левее |
||||||
точки x0 |
(рис. 23.3). Тогда, очевидно, ξ − x0 < 0 |
и |
x − x0 < 0 . |
|||||
|
|
ξ |
η |
|
|
|
|
|
|
a |
x |
|
|
x0 |
|
|
b |
|
|
|
Рис. 23.3 |
|
|
|
|
|
|
|
|
162 |
|
|
|
|
|
Если же точка x расположена правее точки x0 (рис. 23.4), то картина будет следующей:
|
|
|
|
|
|
η |
|
|
|
ξ |
|
|
|
|
|
|
a |
|
x0 |
|
|
|
|
|
x |
b |
|
||
|
|
|
|
|
|
|
|
|
Рис. 23.4 |
|
|
|
||
В |
|
этом случае |
|
ξ − x0 > 0 |
и |
x = x0 > 0 . Таким |
образом, |
|||||||
(ξ − x0 )(x − x0 ) > 0 в |
|
любом |
|
случае |
и |
знак |
разности |
|||||||
R(x) = |
f |
′′ |
|
|
определяется только знаком второй производ- |
|||||||||
(η)(ξ − x0 )(x − x0 ) |
||||||||||||||
ной, откуда и следует доказываемое утверждение. |
|
|
||||||||||||
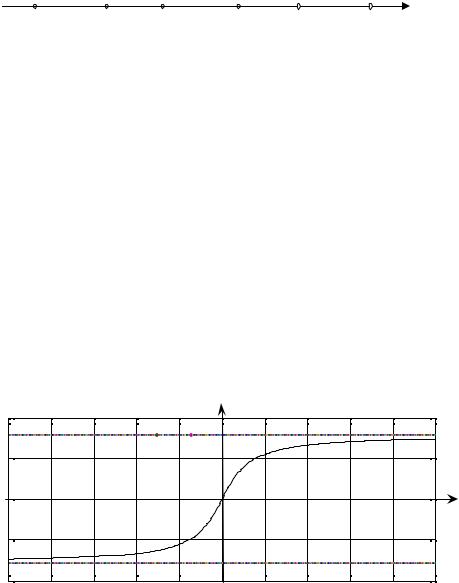
Например, для функции y = arctg x |
|
имеем: |
|
|
|
|||||||||
|
|
|
|
1 |
|
y′′ = |
|
−2x |
|
> 0, |
x < 0 |
|
||
|
|
y′ = |
|
|
, |
|
|
|
, |
y′′ |
< 0, x > 0 |
|
||
|
|
|
+ x2 |
|
+ x2 )2 |
|
||||||||
|
|
1 |
|
(1 |
|
|
|
|||||||
Поэтому график этой функции обращён выпуклостью вниз при отрицательных значениях аргумента и выпуклостью вверх при его положительных значениях.
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
-2 |
-8 |
-6 |
-4 |
-2 |
0 |
2 |
4 |
6 |
8 |
10 |
-10 |
Рис. 23.5
23.2. Точки перегиба. Точки графика функции, в которых направление выпуклости меняется на противоположное, называют точками перегиба. Например, у синусоиды это точки пересечения её графика с осью абсцисс. Необходимым условием существования точки перегиба графика дважды дифференцируемой функции является равенство нулю её второй производной в некоторой точке, а достаточным – перемена знака второй производной при «переходе» через эту точку. Найдем, например, точки перегиба кривой
163
|
|
|
y = |
|
1 |
|
. |
|
|
|
|
||
|
|
|
1 + x2 |
|
|
|
|
||||||
Для этой функции имеем |
|
−2x |
|
|
|
|
|
|
|
− 1 |
|
||
|
′ |
|
|
|
′′ |
|
3x2 |
||||||
y |
= (1 + x2 )2 |
, y |
= (1 |
+ x2 )3 . |
|||||||||
|
|
|
|||||||||||
Следовательно, точками перегиба могут быть только точки
P |
= |
|
|
1 |
|
, |
3 |
. |
|
|
|
|
|
|
|||||
|
|
|
|||||||
1,2 |
|
|
3 |
4 |
|
||||
|
|
|
|
|
|||||
При переходе через каждую из них вторая производная меняет знак, значит эти точки – точки перегиба (см. рис. 22.2).
При построении графиков полезно вычислить значение первой производной в точке перегиба, дающее направление касательной, относитель-
′ |
|
.Кроме |
но которой происходит перегиб. В нашем примере y (P ) ≈ ± 0, 65 |
||
|
1,2 |
|
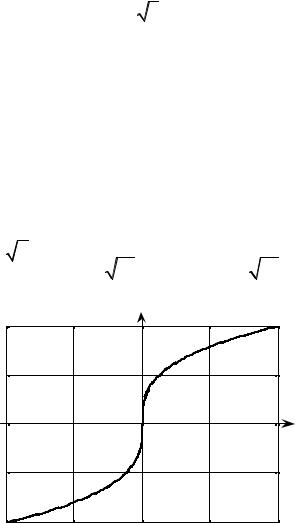
того заметим, что в точках перегиба вторая производная может и не существовать, что видно на графике следующей функции
y = 3 |
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|
|
|||
|
|
|
|
|
|
|||||||||||
x , y′ = |
|
|
|
> 0, y′′ = − |
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
3 |
x |
2 |
|
|
9 x |
3 |
x |
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
1
0.5 |
|
|
|
|
0 |
|
|
|
|
-0.5 |
|
|
|
|
-1 |
-0.5 |
0 |
0.5 |
1 |
-1 |
Рис. 23.6
23.3. Асимптоты. Иногда кривая, имеющая бесконечную ветвь, при удалении её точек в бесконечность «как бы выпрямляется» и приближается к некоторой прямой. Эту прямую называют асимптотой кривой (греч. asymptotos – несливающаяся). Если авторы этого термина подчеркивали то, что кривая не сливается с прямой, то мы обращаем внимание на то, что
164
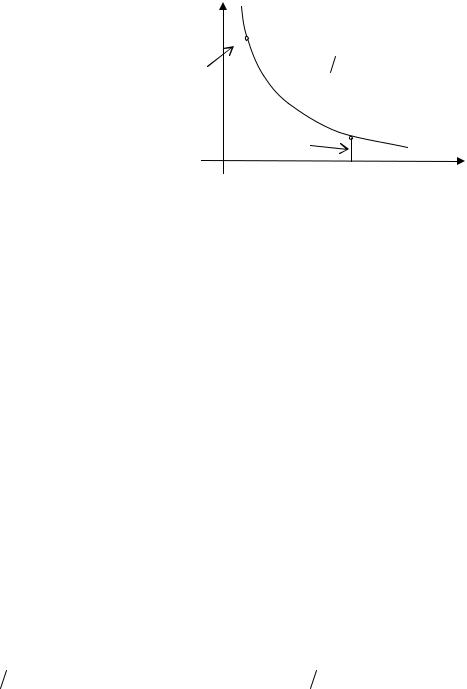
расстояние точки кривой (x, f (x)) до прямой – асимптоты стремится к нулю при движении точки вдоль кривой к бесконечности. Пример кривой, имеющей асимптоты, даёт график функции y = 1 x
x
|
|
|
M (x, y) |
|
|
|
|
|
|
|
|
d = x |
|
|
y = 1 x |
|
|
|
|
N(x, y)
d = y
Рис. 23.7
Рассмотрим одну из ветвей этой кривой. Когда точка M (x, y) стремится к бесконечности, то расстояние её до оси Oy , равное d = x , стремится к нулю. Значит прямая x = 0 – вертикальная асимптота. Если N(x, y) → ∞, то d = y → 0 . Следовательно, прямая y = 0 – горизонтальная асимптота. Как найти вертикальные асимптоты кривой, заданной уравнением y = f (x)? Необходимым условием для этого является существование точек разрыва функции. Достаточным условием будет одно из следующих:
lim f (x) = ± ∞ ,
x→x0 ±0
где x0 точка разрыва.
Горизонтальные асимптоты кривых, определённых в бесконечном промежутке, определяются существованием конечных пределов:
lim |
f (x) = a , |
lim |
f (x) = b . |
|
x→+∞ |
|
x→−∞ |
|
|
В этом случае прямые y = a |
и y = b – |
горизонтальные асимптоты. На- |
||
пример, график функции y = arctg x |
при |
x → + ∞ |
имеет асимптоту |
|
y = π 2 , а при x → − ∞ асимптоту y = − π 2 |
(см. рис. 23.5). |
|||
Пусть кривая, заданная уравнением |
y = f (x) , |
имеет наклонную |
||
асимптоту y = k x + b . Как найти величины |
k и b? |
Ограничимся рас- |
||
смотрением случая, когда x → + ∞ . |
|
|
|
|
165

|
y = f (x) |
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
d = MN cos α |
|||
|
|
α |
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
Рис. 23.8 |
|
|
|
|
|
||
Заметим, что d = MN cosα , поэтому |
d |
и |
MN стремятся одновременно |
|||||||
к нулю при |
x → + ∞ , т.к. |
α = const . Значит, если кривая y = f (x) имеет |
||||||||
асимптоту |
y = k x + b , то |
|
|
|
|
|
|
|
|
|
|
lim MN = lim |
[ |
f (x) − k x − b ] = 0. |
(23.1) |
||||||
|
x→+∞ |
x→+∞ |
|
|
|
|
|
|
|
|
Преобразуем это выражение к виду |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
f (x) |
|
b |
|||
|
|
|
lim x |
|
− k − |
|
|
= 0 . |
||
|
|
|
|
|
|
|||||
|
|
|
x→+∞ |
|
x |
|
x |
|
||
Для того чтобы произведение двух сомножителей, один из которых стремится к бесконечности, стремилось к нулю, необходимо стремление к нулю второго сомножителя, откуда имеем
k = lim |
f (x) |
. |
(23.2) |
|
|||
x→+∞ |
x |
|
|
При найденном k из (23.1) получим
b = lim [ f (x) − k x] . |
(23.3) |
x→+∞ |
|
Если при x → − ∞ также существует наклонная асимптота, то ее пара- |
|
метры находятся по аналогичным формулам с заменой |
x → +∞ на |
x → − ∞ . Если один из пределов не существует или равен ∞ , то соответст-
вующей асимптоты нет. Например, |
функция y = x 2 не имеет асимптот. |
|||
Или другой пример: для функции y = x + ln x имеем |
||||
k = lim (1 |
+ |
ln x |
) = 1 , b = lim ln x = +∞ , |
|
|
||||
x→+∞ |
|
x |
x→+∞ |
|
|
166 |
|||

т.е. у этой кривой нет наклонной асимптоты. Теперь приведем пример кри- |
|||||||||
вой, имеющей наклонную асимптоту |
|
|
|
|
|
||||
|
|
|
|
y = x2 + 2x −1 . |
|
|
|
||
|
|
|
|
|
x |
|
|
|
|
Для этой функции найдем |
|
|
|
|
|
|
|
||
|
x2 |
+ 2x −1 |
= 1 , b |
= lim |
x2 |
+ 2x − 1 |
|
= 2 |
|
|
k = lim |
x |
2 |
|
x |
− x |
|||
|
x→±∞ |
|
|
x→±∞ |
|
|
|
||
и приведем графики функции и её наклонной асимптоты |
y = x + 2 |
||||||||
Используя свойство асимптоты, найдем |
|
|
|
|
|||||
|
x2 + 2x − 1 |
≈ (x + 2) x=2016 = 2018. |
|
||||||
|
|
x |
|
|
|||||
|
|
|
x=2016 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
10 |
y = x2 + 2 x − 1 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
y = x + 2 |
|
||
4 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
|
-6 |
|
|
|
|
|
|
|
|
|
-8 |
|
|
|
|
|
|
|
|
|
-4 |
-3 |
-2 |
|
-1 |
0 |
1 |
2 |
3 |
4 |
|
|
|
|
Рис. 23.9 |
|
|
|
|
|
23.4. Примерный план исследования функции. Приведём краткий |
|||||||||
перечень вопросов, на которые нужно ответить при исследовании функ- |
|||||||||
ции. |
|
|
|
|
|
|
|
|
|
1. Область определения. Чётность, нечётность, периодичность. Ис- |
|||||||||
следование в окрестности точек разрыва (возможны вертикальные |
|||||||||
167
асимптоты). Точки пересечения с осями, поведение на бесконечности (возможны горизонтальные асимптоты).
2.Экстремумы. Интервалы возрастания и убывания (различать «гладкие» экстремумы и «остриё» или излом).
3.Точки перегиба, интервалы выпуклости (полезно вычислить производную в точке перегиба)
4.Наклонные асимптоты.
Заметим, что перечисленный порядок вопросов совсем не обязатель-
ный.
168

Лекция 24. Кривизна. Приближённое решение уравнений
24.1. Понятие кривизны. Одна и та же кривая в разных точках искривлена по-разному. Например, синусоида в точках пересечения с осью абсцисс почти прямая, а в вершинах дуг наиболее искривлена. Более того, на различных участках она искривлена в разном направлении. Нельзя ли как-то определить кривизну в данной точке кривой? Оказывается можно. Для этого определим сначала среднюю кривизну некоторого участка кривой.
Пусть при перемещении точки по кривой из положения M1 в положение M 2 касательный вектор повернётся на угол Δα. Обозначим прой-
денное расстояние через |
s . |
Ясно, что Δα есть функция |
s (см. рис. |
|||||||
24.1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Δα |
|
|
|
|
|
|
|
|
|
M 2 |
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
M1 |
|
α |
|
|
|
|
|
|
|
|
|
|
Рис. 24.1 |
|
|
|
|
||
Отношение |
|
|
|
Δα = k |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
s |
cp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
назовём средней кривизной участка кривой |
s . |
|
||||||||
Рассмотрим некоторые примеры. Перемещение точки вдоль прямой |
||||||||||
на расстояние |
s не |
меняет направления касательного вектора, т.е. |
||||||||
Δα = 0 . Таким образом, |
средняя кривизна любого участка прямой линии |
|||||||||
равна нулю, что не противоречит здравому смыслу. |
|
|||||||||
Пусть теперь точка «прошла» некоторую дугу s окружности радиу- |
||||||||||
са R . Поскольку длина дуги окружности с центральным углом |
Δα равна |
|||||||||
s = RΔα, то средняя кривизна любой части окружности равна |
|
|||||||||
|
|
|
k = Δα |
= |
Δα |
= |
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
cp |
s |
|
R s |
|
R |
|
|
|
|
|
|
|
|
|
||||
169
