
9714
.pdf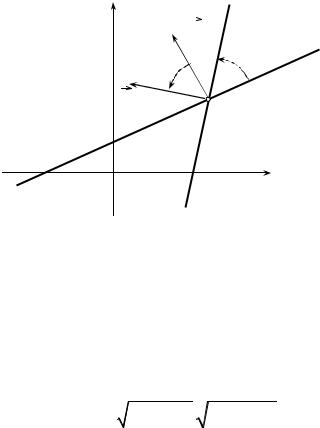
[Введите текст]
Вернемся к формуле (10.1) и получим условия перпендикулярности и параллельности двух прямых y = k1x + b1 , y = k2 x + b2 , выраженные через их угловые коэффициенты:
L |
L |
k |
2 |
= − |
1 |
; |
L |
|
|
|
L |
|
k = k |
2 |
. |
|||
|
|
|||||||||||||||||
|
||||||||||||||||||
1 |
2 |
|
|
|
|
k1 |
1 |
|
|
|
2 |
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
b1 = b2 , то |
|
|
|
||||||
В последнем случае, если дополнительно |
|
прямые L1 и L2 сов- |
||||||||||||||||
падают. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть теперь прямые |
L1 и |
L2 |
заданы общими уравнениями |
|||||||||||||||
A1x + B1 y + C1 = 0 , |
A2 x + B2 y + C2 = 0 . |
|
|
(10.2) |
||||||||||||||
Сведём вычисление угла α между прямыми к вычислению угла ϕ между нормальными векторами к этим прямым. Заметим, что угол между прямыми может быть только острым, а угол между векторами может быть и тупым. Поэтому, если угол ϕ между векторами N1 = { A1, B 1} и N2 = { A2 , B 2}
острый, то α = ϕ (см. рис.10.3).
y |
|
|
L2 |
|
N1 |
|
|
ϕ |
α |
|
L1 |
||
|
||
N2 |
|
O |
x |
|
Рис. 10.3 |
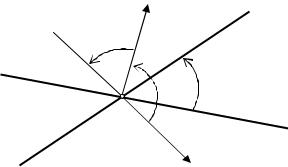
Если же угол ϕ между нормальными векторами тупой, то α = π − ϕ (см.
рис. 10.4). Поскольку cos α = − cos ϕ , |
то |
cosα =| cosϕ | . Таким образом, |
||||||
для вычисления угла между прямыми получаем формулу |
||||||||
cos α = |
|
| A1 A2 + B1B2 | |
||||||
|
|
|
|
|
|
|
|
|
A 2 |
+ B 2 |
|
A 2 |
+ B 2 |
||||
|
|
|
||||||
|
|
1 |
1 |
2 |
2 |
|
|
|
70
[Введите текст]
αN2 L1
|
|
|
|
|
|
|
|
|
|
ϕ |
|
α |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
L2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N1 |
|
|
|
|
|
|
|
|
Рис. 10.4 |
|
|
|
|
|||||
В частности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
L1 L2 A1 A2 + B1B2 = 0 ; |
|
||||||||||||||
L |
|
|
|
L |
|
|
|
A1 |
= |
B1 |
. |
|
|||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
2 |
|
|
|
|
A2 |
|
B2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
В последнем случае, если дополнительно выполняется равенство |
|
||||||||||||||
|
|
|
|
|
A1 |
= |
B1 |
= |
C1 |
|
, |
|
|
(10.3) |
|
|
|
|
|
|
A2 |
B2 |
C2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
то эти прямые совпадают.
Обратим внимание на связь полученных условий взаимного расположения прямых с условиями разрешимости системы (10.2) двух линейных уравнений с двумя неизвестными. Определитель этой системы
|
= |
A1 |
B1 |
= A B − A B . |
|||
|
|
A2 |
B2 |
1 |
2 |
2 |
1 |
|
|
|
|
|
|
||
Если |
¹ 0 , то, как известно, |
система имеет единственное решение, |
|||||
которому |
соответствует точка пересечения прямых L1 и L2 . Если D = 0 , |
||||||
то выполнено условие параллельности этих прямых. При этом возможны два случая. В первом, когда выполнено условие (10.3), прямые совпадают, и система имеет бесконечное множество решений (координаты любой точки прямой дают решение системы). Отметим, что условие (10.3) означает, что ранг расширенной матрицы совпадает с рангом матрицы системы, т.е.
rang A1 |
B1 |
C1 |
= rang A1 |
B1 = 1, |
A2 |
B2 |
C2 |
A2 |
B2 |
|
|
71 |
|
|
[Введите текст]
и согласно теореме Кронекера-Капелли система совместна. Во втором случае, когда в условии (10.3) не выполнено второе равенство, прямые параллельны, ранг расширенной матрицы больше ранга матрицы системы, и система несовместна.
10.2. Пучок прямых, определяемый двумя пересекающимися прямыми. Иногда при решении задач не следует спешить с нахождением точки пересечения двух прямых, решая систему уравнений (10.2), а лучше воспользоваться понятием пучка прямых, проходящих через точку пе-
ресечения этих прямых (в частности, когда нужно найти прямую, проходящую через точку пересечения данных прямых, и удовлетворяющую некоторому дополнительному условию). Уравнение пучка прямых, проходящих через точку пересечения двух заданных прямых
A1x + B1 y + C1 = 0 , |
A2 x + B2 y + C2 = 0 |
|
имеет вид |
|
|
( A1x + B1 y + C1 ) + λ( A2 x + B2 y + C2 ) = 0 . |
(10.4) |
|
Действительно, уравнение (10.4) – |
уравнение прямой. Так как точка |
|
пересечения этих прямых M 0 ( x0 , y0 ) принадлежит каждой из этих прямых, то ее координаты обращают в ноль обе скобки в (10.4), а, значит, при любом λ прямая (10.4) проходит через точку M 0 .
10.3. Расстояние от точки до прямой. Пусть требуется вычислить расстояние от точки M 0 ( x0 , y0 ) до прямой Ax + By + C = 0 .
2
d |
0 |
x
Рис. 10.5
Пусть M 1 ( x1, y1 ) – проекция точки M 0 на прямую (см. рис. 10.5). Ис-
комое расстояние равно абсолютной величине проекции вектора M1M0 на направление нормального вектора N = { A, B } .
72

[Введите текст]
|
|
UUUUUUR |
|
|
< |
|
N ,M |
|
M |
|
|
> |
|
|
|
|
A( x0 − x1 |
) + |
B( y0 − y1 ) |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
d = |
R |
M 1M 0 |
|
= |
|
|
|
|
|
|
|
|
|
R1 |
|
|
|
|
0 |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
= |
|
|||||
ПрN |
|
|
|
|
|
|
| N | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| N | |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
= |
|
|
Ax |
|
|
|
+ By |
|
− Ax − By |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
R |
|
|
1 |
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| N | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как точка |
M 1 ( x1, y1 ) |
|
принадлежит прямой, то |
Ax1 + By1 = −C , |
|
|||||||||||||||||||||||||||||||||||||||||||
поэтому окончательно получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
d = |
|
|
Ax0 + By0 |
|
|
+ C |
|
|
. |
|
|
|
|
|
|
(10.5) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
+ B2 |
|
|
|
|
|
|
|
|
||||||||||||||
Найдём координаты точки M 1 ( x1, y1 ) . Для этого выразим вектор |
||||||||||||||||||||||||||||||||||||||||||||||||
M1M0 через найденное расстояние |
d |
|
и единичный вектор |
|
N / | N |, |
нор- |
||||||||||||||||||||||||||||||||||||||||||
мальный к прямой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
UUUUUUR |
= ± |
|
d |
|
|
R |
|
|
|
|
|
|
(10.6) |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
M |
M |
0 |
|
|
|
R |
|
N . |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
| N | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из формулы (10.5) видно, что знак проекции вектора M1M0 |
|
определяется |
||||||||||||||||||||||||||||||||||||||||||||||
знаком выражения Ax0 + By0 + C , |
|
т.е., |
|
|
|
если |
|
|
|
|
Ax0 + By0 + C > 0 , |
то |
||||||||||||||||||||||||||||||||||||
M1M 0 -- N и в формуле (10.6) нужно взять знак плюс. |
3x − 4y + 4 = 0 |
|||||||||||||||||||||||||||||||||||||||||||||||
Пример. |
Найти проекцию точки |
|
|
M 0 (1,8) на прямую |
||||||||||||||||||||||||||||||||||||||||||||
Вычисляем расстояние точки |
|
|
M 0 |
до прямой |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
d = |
|
|
3 ×1 - 4 × 8 + 4 |
|
|
= |
| -25 | |
= 5 . |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 + 42 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||||||||||||||||
Попутно выясняется, что M1M 0 -¯ N , поэтому формула (10.6) даёт равен- |
||||||||||||||||||||||||||||||||||||||||||||||||
ство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UUUUUUR |
= {1 |
− x ; 8 − y } = − |
5 |
{3; 4}. |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
M |
M |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
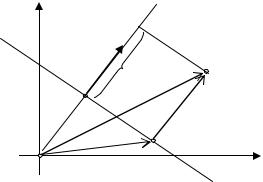
Отсюда, приравнивая координаты векторов, получаем координаты точки
M1(4, 4) (см. рис. 10.6).
73
[Введите текст]
M 0 (1, 8)
M1 (?,?) |
N = {3; |
−4} |
|
|
Рис. 10.6
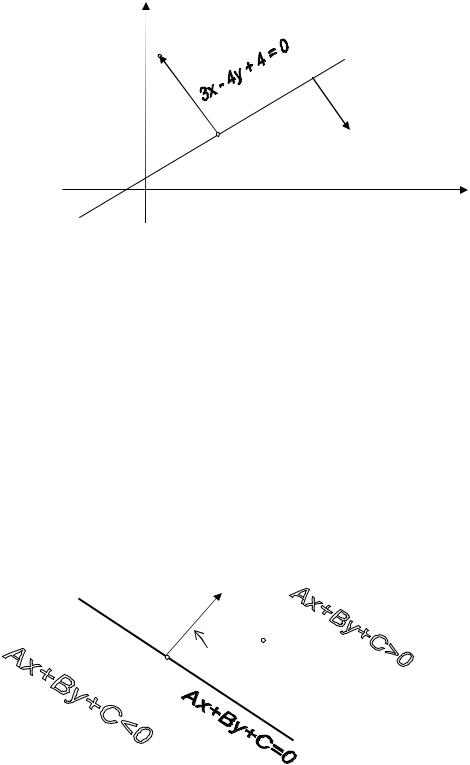
10.4. Линейные неравенства. В заключение этой лекции выясним геометрический смысл неравенства
Ax + By + C > 0 . |
(10.7) |
Построим прямую |
|
Ax + By + C = 0 |
(10.8) |
и нормальный к ней вектор N = { A, B } . Нас интересует множество точек |
|
M (x, y) , координаты которых удовлетворяют |
неравенству (10.7). Возь- |
мём на прямой (10.8) произвольную, но фиксированную точку M 0 ( x0 , y0 ) .
N
ϕ
 M ( x, y )
M ( x, y )
M 0
Рис. 10.7
Поскольку Ax0 + By0 + C = 0 , то, выражая отсюда C и подставляя в (10.7), получим, что левая часть этого неравенства (10.7) равна скалярному про-
изведению вектора N = { A, B } на вектор M 0M
74
[Введите текст]
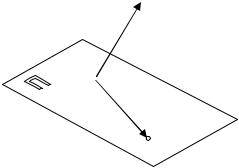
< N , M 0 M > = A(x − x0 ) + B( y − y0 ) > 0 .
Итак, неравенству (10.7) удовлетворяют все точки плоскости, для ко-
торых угол между векторами N и M 0M – острый. Из рисунка 10.7 видно, что все такие точки принадлежат одной полуплоскости. Чтобы выяснить, какая из двух полуплоскостей «отвечает» неравенству (10.7), достаточно проверить его выполнение для какой-нибудь одной точки из любой полуплоскости. Если координаты этой точки ему удовлетворяют, то и координаты всех точек полуплоскости, в которой выбрана «пробная» точка, будут его решениями, если нет – то нужная полуплоскость – другая.
75
[Введите текст]
Лекция 11. Плоскость
11.1. Различные виды уравнения плоскости. Перейдем теперь к изучению уравнений плоскости в пространстве. Пусть в трехмерном пространстве с декартовой прямоугольной системой координат имеем плоскость П , и мы хотим получить уравнение, связывающее координаты любой точки, принадлежащей этой плоскости.
N
M 0
 900
900
M
Рис. 11.1 |
|
Для этого зафиксируем какую-нибудь точку M 0 ( x0 , y0 , z0 ) П |
и |
возьмем вектор, перпендикулярный (ортогональный, нормальный) к этой плоскости. Пусть это будет вектор N = { A, B,C} . Очевидно, что для про-
извольной точки M (x, y, z) П векторы M 0M = { x − x0 ; y − y0 ; z − z0 } и N перпендикулярны, т.е. их скалярное произведение равно нулю
< N , M0M > = 0
или в координатах
A( x − x0 ) + B( y − y0 ) + C( z − z0 ) = 0 . |
(11.1) |
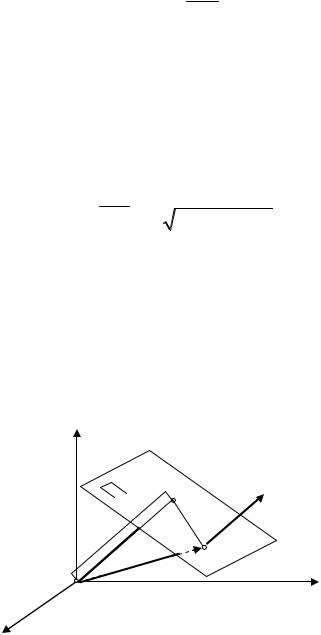
Это и есть уравнение плоскости П , проходящей через заданную точку M 0 ( x0 , y0 , z0 ) перпендикулярно заданному вектору N = { A, B,C} .
Раскрывая в (11.1) скобки, получим уравнение |
|
Ax + By + Cz + D = 0 , |
(11.2) |
где для краткости обозначено D = − Ax0 − By0 − Cz0 . Уравнение (11.2) называют общим уравнением плоскости. Обратим внимание, что уравнение
плоскости является линейным |
уравнением относительно переменных |
x, y, z , а коэффициенты при них – |
соответствующие координаты нормаль- |
ного вектора к этой плоскости. |
|
|
76 |
[Введите текст]
Обратно, покажем, что уравнение вида (11.2) определяет плоскость и построим её. По данным числам A, B,C построим вектор N = { A, B,C}
и введем радиус-вектор r = { x, y, z} . Тогда уравнение (11.2) можно пред-
ставить в виде
R |
> + D = 0 |
или |
| N | ПрR |
R |
|||||||
< N , r |
r = −D . |
||||||||||
|
|
|
|
|
|
|
|
N |
|
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
= − |
D |
, |
|
|
|
||
|
|
|
R |
R |
|
|
|
||||
|
|
ПрN r |
|
|
|
|
|||||
|
|
|
|
|
|
| N | |
|
|
|
||
т.е. все радиус-векторы |
R |
|
|
координаты которых удовлетворяют |
|||||||
r = { x, y,z} , |
|||||||||||
уравнению (11.2), имеют одну и ту же проекцию на вектор N = { A, B,C} . |
|||||||||||
Это означает, что точки |
M (x, y, z) принадлежат плоскости, перпендику- |
||||||||||
лярной вектору N = { A, B,C} |
и отстоящей от начала координат на рас- |
||||||||||
стояние | p | , где |
|
|
|
|
|
|
|
|
|
|
|
|
p = − |
D |
= − |
|
|
|
D |
|
|
. |
|
|
R |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
+ B2 + C 2 |
|
||||||||
|
|
| N | |
|
|
|
A2 |
|
|
|
||
Отсюда следует алгоритм построения плоскости по заданному уравнению (11.2). Через начало координат проведем прямую в направлении
вектора |
N = { A, B,C} и отложим на ней от начала координат отрезок OP |
|
длиной |
| p | в направлении вектора |
N = { A, B,C} , если p > 0 , или в про- |
тивоположном направлении, если |
p < 0 . Через конец этого отрезка P |
|
проводим перпендикулярно ему требуемую плоскость.
z
P N
p |
M |
y |
|
O r
x
Рис. 11.2
Рассмотрим некоторые частные случаи общего уравнения плоскости. Пусть один из коэффициентов перед переменными в уравнении (11.2) равен нулю (например, C = 0 ). Тогда нормальный вектор этой плоскости
77
[Введите текст]
N = {A, B,0}. Это значит, что он перпендикулярен оси O z , а плоскость параллельна этой оси
z
|
O |
|
y |
x |
N = {A, B,0} |
Рис. 11.3
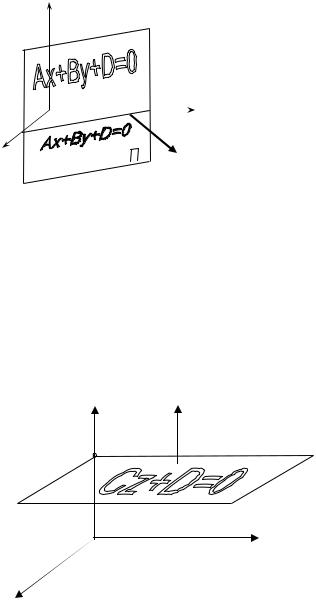
Теперь пусть два каких-нибудь коэффициента перед переменными в уравнении (11.2) равны нулю (например, A = B = 0 ). Тогда нормальный
вектор N = {0,0,C} перпендикулярен плоскости xO y , а плоскость параллельна этой координатной плоскости
z N = {0,0,C}
O
y
x
Рис. 11.4
Рассмотрим ещё случай, когда в уравнении (11.2) D = 0 . Это означает, что точка (0,0,0) принадлежит плоскости
Ax + By + Cz = 0
или, другими словами, эта плоскость проходит через начало координат. Для наглядного представления расположения этой плоскости найдем
её следы, т.е. линии пересечения с координатными плоскостями (см. рис. 11.5).
78

[Введите текст]
Ax + By = 0 |
, |
Ax + Cz = 0 |
, |
By + Cz = 0 |
|||
|
z = 0 |
|
y = 0 |
|
. |
||
|
|
|
|
|
x = 0 |
||
z
y
x
Рис. 11.5
Из общего уравнения плоскости легко получить так называемое
уравнение плоскости в отрезках
|
x |
+ |
y |
+ |
z |
= 1, |
(11.3) |
|
|
|
|
||||
|
a b c |
|
|||||
где (a,0,0) , (0,b,0) и (0,0,c) – точки пересечения плоскости |
с координат- |
||||||
ными осями. Действительно, из (11.2) следует Ax + By + Cz = −D и далее, предполагая, что D ¹ 0 (т.е. плоскость не проходит через начало координат) и разделив обе части этого уравнения на − D , получим уравнение
(11.3), в котором a = − |
D |
, |
b = − |
D |
и c = − |
D |
величины отрезков, которые |
|
A |
|
B |
|
C |
||
плоскость «отрезает» от осей координат (см. рис. 11.6).
z
c
b
y
x |
a |
|
Рис. 11.6
79
