
9714
.pdf
[Введите текст]
Лекция 31. Комплексные числа
31.1. Введение. Вспомним, как развивалось понятие числа, начиная от чисел натуральных до чисел действительных. Если операция сложения во множестве натуральных чисел выполнима без ограничений, то операция обратная сложению, т.е. решение уравнения a + x = b , выполнима только при b > a . Если отказаться от этого ограничения, то получатся «новые» числа – отрицательные. Так «родились» целые числа, во множестве которых сохранены все свойства суммы и обратная операция – разность, результатом которой является число x = b - a .
Во множестве натуральных чисел также не всегда разрешима задача, обратная операции умножения, т.е. решение уравнения a × x = b . Для её решения необходимо и достаточно, чтобы b было кратно a . Возникла необходимость расширения множества целых чисел до чисел рациональных. В этом множестве обратная операция – деление, результатом которой является число x = b : a , разрешима с ограничением a ¹ 0 . Для рациональных чисел сохраняются свойства операций сложения и умножения.
Оказалось, что во множестве рациональных чисел не всегда разрешима задача извлечения квадратного корня из положительного числа, например, неразрешимо уравнение x2 − 2 = 0 . Число 
 2 , которым мы привычно обозначаем один из корней этого уравнения, число – иррациональное. Это число «должно» бы выражать длину диагонали квадрата со стороной равной единице. Но среди известных чисел, с помощью которых можно выразить длину диагонали, такого числа не нашлось. Такие числа назвали иррациональными, т.е. невыразимыми. Это открытие было сделано во времена Пифагора (580–500 г. до н.э.). Позднее, примерно через 1000 лет, латинские слова рациональный и иррациональный стали связывать со словом рацио – разум. В средневековой математической культуре возник новый термин вместо «иррациональный» – surdus ( глухой или немой), т.е. такое число, когда немой его не может высказать другому, а второй (глухой) не может выслушать первого. Сопротивление «разума» исчезло, когда стали интерпретировать иррациональные числа бесконечными десятичными непериодическими дробями.
2 , которым мы привычно обозначаем один из корней этого уравнения, число – иррациональное. Это число «должно» бы выражать длину диагонали квадрата со стороной равной единице. Но среди известных чисел, с помощью которых можно выразить длину диагонали, такого числа не нашлось. Такие числа назвали иррациональными, т.е. невыразимыми. Это открытие было сделано во времена Пифагора (580–500 г. до н.э.). Позднее, примерно через 1000 лет, латинские слова рациональный и иррациональный стали связывать со словом рацио – разум. В средневековой математической культуре возник новый термин вместо «иррациональный» – surdus ( глухой или немой), т.е. такое число, когда немой его не может высказать другому, а второй (глухой) не может выслушать первого. Сопротивление «разума» исчезло, когда стали интерпретировать иррациональные числа бесконечными десятичными непериодическими дробями.
Комплексные числа, о которых пойдет речь, возникли из необходимости извлечения квадратного корня из отрицательного числа. Определим
«новое» |
число –« мнимую единицу» i , квадрат которого равен |
−1, т.е. |
||||
i 2= −1. |
Расширим множество действительных чисел, вводя числа вида |
|||||
z = x + iy , которые будем |
называть |
комплексными. |
Число |
|||
x = Re z = Re(x + iy) |
называют |
действительной |
(лат. realis– |
действитель- |
||
ный) частью комплексного числа, а число y = Im z = Im(x + iy) |
его мнимой |
|||||
(лат. imaginarius – |
мнимый) частью. |
|
|
|
||
|
|
|
220 |
|
|
|
[Введите текст]
31.2. Геометрическая интерпретация комплексных чисел. Ком-
плексные числа удобно изображать точками плоскости xOy , с декартовой системой координат, которую в этом случае называют комплексной плоскостью. Ось абсцисс этой плоскости называют действительной осью
– ей отвечают действительные числа z = x , а ось ординат – мнимой осью. Числа z = iy , лежащие на мнимой оси, называют чисто мнимыми.
Два комплексных числа z1 = x1 + iy1 и z2 = x2 + iy2 равны тогда и толь-
ко тогда, когда x1 = x2 и y1 = y2
Сопряжённым к данному комплексному числу z = x + iy назовем число z = x − iy , которое обычно помечается чертой сверху. Сопряжённые комплексные числа отличаются знаком мнимой части. Если z = x − iy , то z = x + iy . Сопряжённые числа симметричны относительно действительной оси (см. рис. 31.1).
|
|
z1 = x1 + iy1 |
|
|
= x2 + iy2 |
|
|
|
|
|
z2 |
||
i |
|
|
|
y2 |
||
|
|
|
|
|||
|
|
|
x2 |
|
||
|
|
|
|
z2 |
= x2 − iy2 |
|
|
|
|
||||
|
|
z1 = x1 − iy1 |
|
|||
|
Рис. 31.1 |
|
||||
31.3. Тригонометрическая форма комплексного числа. Наряду с
алгебраической формой комплексного числа z = x + iy введем его тригонометрическую форму. Будем интерпретировать комплексное число
z = x + iy |
как радиус-вектор точки ( x, y) . Модулем r комплексного числа |
||
|
называют длину этого вектора r =| z |= |
|
(см. рис. 31.2) . |
z = x + iy |
x2 + y2 |
||
Модуль – |
это расстояние от начала координат до точки z = ( x, y) . |
||
Угол ϕ между положительным направлением оси Ox и радиус- |
|||
вектором |
z называется аргументом комплексного числа. Поскольку этот |
||
угол определяется с точностью до числа, кратного 2π, то выделим его
главную ветвь 0 ≤ argz < 2π . |
Значение ϕ = arg z определяется как решение |
|||||||||
системы уравнений |
|
|
|
|
|
|
|
|
||
|
|
|
x |
y |
|
|||||
cosϕ = |
|
|
|
|
; sin ϕ = |
|
|
|
; 0 |
≤ ϕ < 2π . |
|
|
|
|
|
|
|
||||
|
|
|
||||||||
|
|
x2 |
+ y2 |
x2 + y2 |
|
|||||
221
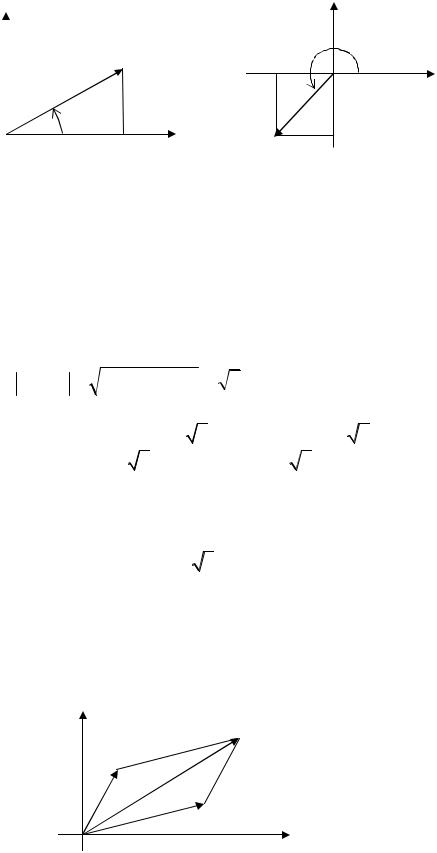
[Введите текст]
z = x + iy |
ϕ = |
5 |
π |
|
|||
−1 |
4 |
|
|
r |
y |
|
ϕ |
||
−i |
||
|
||
x |
z = −1 − i |
Рис. 31.2
От алгебраической формы комплексного числа легко перейти к его тригонометрической форме
z = x + i × y = r cos ϕ + ir sin ϕ = r (cos ϕ + i sin ϕ) .
Пример. Представить число z = −1 − i в тригонометрической форме.
Модуль r = −1− i = 
 (−1)2 + (−1)2 =
(−1)2 + (−1)2 = 
 2 . Аргумент находим, выбирая из решений уравнений
2 . Аргумент находим, выбирая из решений уравнений
cosϕ = |
− |
1 |
|
= − |
|
|
2 |
|
; |
sin ϕ = |
− |
1 |
|
= − |
|
2 |
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||
то, которое попадает в промежуток |
0 ≤ ϕ < 2π . |
|
|
Это угол |
ϕ = |
5 |
π = 2250 |
||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
(см. рис. 31.2). Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
z = −1 − i = |
|
|
|
(cos |
5 |
π + i sin |
5 |
π) . |
|
|
|
||||||||||||||||
|
|
2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
||||
31.4. Операции над комплексными числами. Начнем со сложения. |
|||||||||||||||||||||||||||
Суммой (разностью) двух комплексных чисел |
|
|
z1 = x1 + iy1 |
и z2 = x2 + iy2 |
|||||||||||||||||||||||
называется комплексное число z = z1 ± z2 = (x1 ± x2 ) + i( y1 ± y2 ) |
|
|
|
||||||||||||||||||||||||
y
(x1 + x2 , y1 + y2 )
( x2 , y2 )
(x1 , y1 )
x
Рис. 31.3
Заметим, что это соответствует правилу сложения векторов (см. рис. 31.3).
222
[Введите текст]
Произведением комплексных чисел называется число
(x1 + iy1 ) × (x2 + iy2 ) = (x1x2 - y1y2 ) + i(x1 y2 + x2 y1 ) .
Найдём произведение двух комплексных чисел, заданных в тригонометрической форме
z1 × z2 = r1 (cos ϕ1 + i sin ϕ1) × r2 (cosϕ2 + i sin ϕ2 ) =
= r1 × r2 (cos j1 cos j2 - sin j1 sin j2 + i(sin j1 cos j2 + cos j1 sin j2 )) =
= r1r2 (cos( j1 + j2 ) + i(sin(j1 + j2 )) .
Таким образом, при умножении комплексных чисел в тригонометрической форме их модули нужно перемножить, а аргументы сложить.
Геометрический смысл умножения на комплексное число
z = r (cos ϕ + i sin ϕ)
состоит в том, что происходит «растяжение» плоскости с коэффициентом r и поворот на угол ϕ . Благодаря этим свойствам комплексных чисел с их помощью удаётся решать задачи теории упругости, связанные с деформацией твёрдых тел, а также изучать движение жидкостей и газов.
Пример. Найти произведение чисел z |
= 2(cos(30O + i sin 30O ) и |
1 |
|
z2 = 2(cos(120O + i sin120O ) .Умножение в тригонометрической форме даёт
z z |
2 |
= 4(cos(1500 |
+ i sin1500 ) |
= 4(− |
3 |
+ i 1 ) = −2 3 + 2i . |
|||
1 |
|
|
|
|
2 |
|
2 |
||
|
|
|
|
|
|
|
|||
|
|
|
|
90 |
|
|
|
|
|
|
|
|
120 |
|
60 |
|
|
|
|
|
|
|
4 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
= −2 3 + 2i |
|
|
|
|
|
||
|
|
z = −1 + i 3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|||
3 |
|
|
|
|
|
30 |
|||
|
|
150 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
z |
|
= |
3 + i |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
|
180 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Рис. 31.4 |
|
|
|
|
|
В результате умножения вектора z1 на вектор z2 |
длина вектора z1 уве- |
||||||||
личилась в два раза и он «повернулся» на угол 120O (см. рис. 31.4).
223

[Введите текст]
После этого становится понятными правила умножения отрицательных чисел. Почему, например, (-1) × (-1) = 1 ? Действительно, представляя -1 в тригонометрической форме, получаем
(-1)(-1) = (cos π + i sin π) × (cos π + i sin π) = (cos 2π + i sin 2π) = 1.
Также перестаёт быть «таинственной» формула i 2= -1, поскольку
i × i = (cos π |
+ i sin π)(cos π |
+ i sin π) = (cos p + i sin p) = -1. |
|
2 |
2 |
2 |
2 |
Чтобы получить частное двух комплексных чисел, нужно умно-
жить и числитель и знаменатель дроби на число сопряжённое знаменателю и отделить вещественную и мнимую части.
|
z1 |
|
x1 + iy1 |
|
(x1 + iy1 )(x2 − iy2 ) |
|
x1x2 + y1 y2 |
|
x2 y1 − x1 y2 |
. |
|||||||||||||
z = z |
|
= x |
+ iy |
|
= |
(x |
|
+ iy |
|
)(x |
|
- iy |
|
) |
= |
x2 |
+ y2 |
+ i |
|
||||
2 |
2 |
2 |
2 |
2 |
2 |
x2 |
+ y2 |
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
2 |
2 |
|
2 |
2 |
|
|||||||
Найдём частное двух комплексных чисел, заданных в тригонометрической форме
z1 |
= |
r1 (cos ϕ1 |
+ i sin ϕ1 ) |
= |
r1 |
(cos j |
+ i sin j )(cos j |
2 |
- i sin j |
) = |
|
|
|
|
|||||||
z2 |
|
r2 (cos j2 |
+ i sin j2 ) |
|
r2 |
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
=r1 (cos j1 cos j2 + sin j1 sin j2 + i(sin j1 cos j2 - cosj1 sin j2 )) = r2
=r1 (cos(j1 - j2 ) + i sin(j1 - j2 )). r2
Итак, модуль частного двух комплексных чисел равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
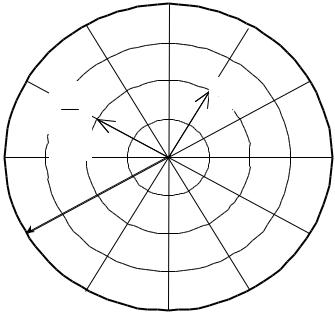
Пример. Найти частное чисел z1 = -2
 3 - 2 × i и z2 =1 + i
3 - 2 × i и z2 =1 + i
 3 . Представим каждое из этих чисел в тригонометрической форме:
3 . Представим каждое из этих чисел в тригонометрической форме:
z |
= 4(cos 2100 + i sin 2100 ) , |
z |
2 |
= 4(cos 600 |
+ i sin 600 ) . |
1 |
|
|
|
|
Тогда частное равно z1 / z2 = 2(cos1500 + i sin1500 ) = -
 3 + i (см. рис. 31.5).
3 + i (см. рис. 31.5).
224
[Введите текст]
|
90 |
120 |
60 |
|
3 |
150 |
2 |
30 |
|
z1 |
z2 |
1 |
|
z2 |
|
180 |
0 |
z 1 |
|
210 |
330 |
240 |
300 |
Рис. 31.5
Определим операцию возведения в степень комплексного числа.
По правилу умножения комплексных чисел в тригонометрической форме для всякого натурального числа n имеем
zn = rn (cos nϕ + i sin nϕ) .
В частном случае, когда модуль числа равен единице, получается формула, носящая имя английского математика А. Муавра (1667-1754)
(cos ϕ + i sin ϕ)n = cos nϕ + i sin nϕ .
Эта формула служит источником для получения многих замечательных соотношений, связывающих тригонометрические функции. Например, при n = 2 имеем равенство
cos2ϕ + 2i sin ϕcos ϕ − sin2ϕ = cos 2ϕ + i sin 2ϕ .
Приравнивая действительные и мнимые части, получаем известные формулы для синуса и косинуса двойного аргумента
cos 2ϕ = cos2ϕ − sin2 ϕ , sin 2ϕ = 2 sin ϕ cos ϕ .
225

[Введите текст]
Лекция 32. Решение алгебраических уравнений
32.1. Извлечение корня из комплексного числа. Число z называется корнем n -ой степени из комплексного числа a , если z n = a . Эта операция – обратная возведению комплексного числа в целую положительную степень. Во множестве вещественных (действительных) чисел эта
задача равносильна задаче нахождения корней уравнения |
|
xn − a = 0 и мы |
||
решали её, раскладывая многочлен xn − a |
на множители. Иногда это уда- |
|||
валось. Например, уравнение x2 − 4 = 0 даёт два корня |
x |
|
= ± 2 , а урав- |
|
|
|
1,2 |
|
|
нение x2 + 1 = 0 корней не имеет. |
a =| a | (cos α + i sin α) и урав- |
|||
Итак, пусть дано комплексное число |
||||
нение z n = a . Будем искать корни этого уравнения среди комплексных чисел, выраженных в тригонометрической форме z = r (cos ϕ + i sin ϕ) , r = ? , ϕ = ? В этой форме уравнение примет вид
rn (cos ϕ + i sin ϕ)n =| a | (cos α + i sin α)
или
rn (cos nϕ + i sin nϕ) =| a | (cos α + i sin α) .
Два комплексных числа в тригонометрической форме равны тогда и только тогда, когда их модули равны, а аргументы отличаются на число, кратное 2π, т.е.
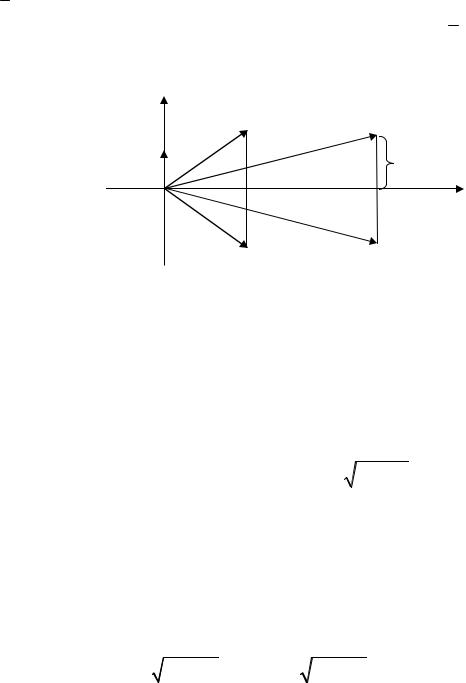
rn =| a |, nϕ = α + 2πk , k = 0, ± 1, ± 2,K.
Поэтому все корни имеют один и тот же модуль r = n | a | , а аргументы
| a | , а аргументы
этих корней определяются по формуле
ϕ = α + 2π k , k = 0, ± 1, ± 2,K. n n
Убедимся, что число корней конечно и равно показателю n степени уравнения. Действительно, представляя искомые корни в тригонометрической форме
|
|
|
|
α |
|
2π |
α |
|
2π |
|
|
|
|
|
|
|
|
|
|||||||
zk |
= n | a | cos( |
|
+ |
|
k ) + i sin( |
+ |
|
k ) |
, |
|||
n |
n |
n |
||||||||||
|
|
|
|
|
n |
|
|
|
||||
видим, что в силу периодичности тригонометрических функций достаточно ограничиться значениями k = 0, ± 1, ± 2,K, n − 1. Если k целое отрицательное, то мы не получим новых корней, так как
z− k = zn−k , k = 1, 2,K, n − 1.
226
[Введите текст] |
|
|
|
|
|
|
|
|
|
|
|
В этом легко убедиться, прибавив |
2π к значению аргумента корня z−k , |
||||||||||
что не меняет значений синуса и косинуса. Например, |
|
||||||||||
|
|
α |
|
2π |
|
α |
|
2π |
|
|
|
cos ϕ− k |
= cos |
|
+ |
|
(−k ) + 2π |
= cos |
+ |
|
(n − k ) |
= cos ϕn−k . |
|
|
|
n |
|||||||||
|
n |
|
n |
|
n |
|
|
|
|||
Итак, мы получили n корней n -й степени из комплексного числа. Это – комплексные числа, модули которых равны r = n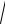 | a | , а аргументы опре-
| a | , а аргументы опре-
деляются формулой ϕ = α + 2π k , k = 0, 1, 2, K, n − 1. Особенно наглядна n n
их геометрическая интерпретация: все корни расположены на окружности,
радиус которой |
r = n |
| a | , и угол между соседними корнями равен 2π . |
|||||
|
|
|
|
|
|
|
n |
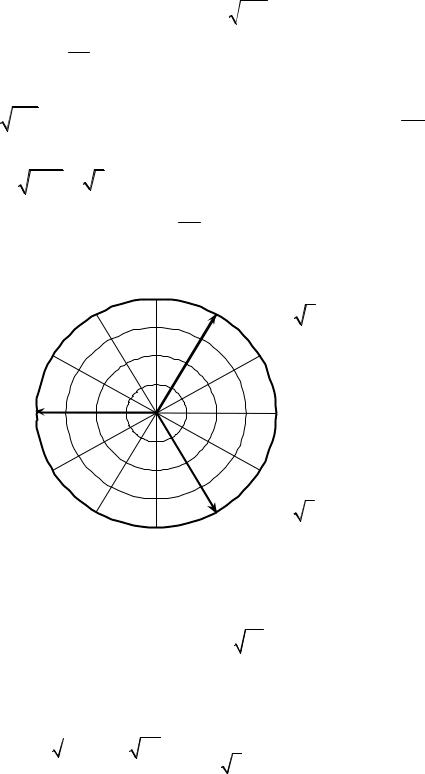
Например, уравнение |
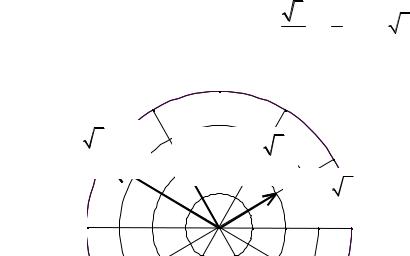
z3 + 8 = 0 имеет три корня, расположенных на ок- |
||||||
ружности радиуса |
r = 3 | -8 | = 3 8 = 2 . Поскольку |
arg(−8) = π , то аргумен- |
|||||
ты корней соответственно равны ϕ |
k |
= π |
+ 2π k , k |
= 0, 1, 2 . |
|
||
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
90 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
60 |
z0 =1+ i |
3 |
|
|
|
|
|
1.5 |
||
|
|
150 |
|
|
1 |
30 |
|
|
|
|
|
|
0.5 |
|
|
z2 = −2 180 |
|
|
|
0 |
|
||
|
|
210 |
|
|
|
330 |
|
|
|
240 |
|
|
300 z3 =1- i |
3 |
|
|
|
|
|
270 |
|
|
|
|
|
|
Рис. 32.1 |
|
|
||
В области действительных чисел символ |
(×) был «закреплён» за |
||||||
положительным корнем из положительного числа. Если расширить его применение для изображения корня из комплексного числа, то он потеряет однозначность. Например,
|
|
|
−2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
−1 = ±i , 3 −8 = |
± i |
|
. |
|||
|
||||||
|
|
|
1 |
3 |
||
|
|
|
|
|
|
|
227 |
|
|
|
|
||
[Введите текст]
32.2. Квадратное уравнение. Рассмотрим квадратное уравнение ax2 + bx + c = 0 , коэффициенты которого действительные числа. Формально написанная формула для вычисления его корней
x = |
-b ± b2 - 4ac |
(32.1) |
|
||
1,2 |
2a |
|
|
|
во множестве действительных чисел не имеет смысла, если подкоренное
выражение |
= b2 − 4ac отрицательно. Но |
теперь мы |
умеем |
находить |
квадратные корни из отрицательных чисел. |
Пусть −d , |
(d > 0) |
некоторое |
|
отрицательное число. Его тригонометрическая форма −d = d (cosπ + i sin π) . Поэтому
|
= |
|
(cos( π |
+ pk ) + i sin( π + pk )), k = 0,1 |
|
= ±i |
|
-d |
d |
-d |
d |
||||
2 |
2 |
|
|
|
|||
Следовательно, если дискриминант уравнения отрицателен, то

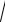 b2 - 4ac =
b2 - 4ac = 
 -(4ac - b2 ) = ±i
-(4ac - b2 ) = ±i
 | b2 - 4ac | .
| b2 - 4ac | .
Формула вычисления корней квадратного уравнения принимает вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
-b ± |
|
|
b2 - 4ac |
|
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
b |
|
- 4ac ³ 0 |
|||
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x1,2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
-b ± i | b2 - 4ac | |
, |
|
b |
2 |
- 4ac < 0 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В случае приведённого квадратного уравнения x2 + px + q = 0 форму- |
||||||||||||||||||||||||||||
лы имеют более компактный вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
p |
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
||
|
- |
± ( |
)2 |
- q , ( |
)2 - q ³ 0 |
|||||||||||||||||||||||
|
|
|
|
2 |
||||||||||||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x1,2 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(32.2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
p |
|
|
|
|
p |
2 |
|
|
|
|
|
|
|
p |
2 |
|
|
|
|
||||||
|
- |
|
|
± i | ( |
|
) |
|
- q | , |
( |
|
) |
|
- q < 0 |
|||||||||||||||
|
2 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
Пример. Решить уравнение z3 + 8 = 0 . После разложения левой части уравнения на множители
(x + 2)(x2 - 2x + 4) = 0
228
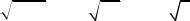
[Введите текст]
становится очевидным действительный корень уравнения x1 = −2 , а два комплексно сопряжённых корня находятся по формуле (32.2)
x2,3 = 1 ± 
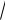 1 − 4 = 1 ±
1 − 4 = 1 ± 
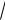 −3 = 1 ± i
−3 = 1 ± i
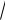 3 .
3 .
Геометрическая интерпретация корней данного уравнения дана на рис. 32.1.
32.3. Разложение многочлена на множители. Рассмотрим многочлен степени n
P (z) = a zn + a zn−1 |
+ K + a |
z + a . |
||
n |
0 |
1 |
n−1 |
n |
Число z1 , обращающее |
этот многочлен в нуль |
( Pn (z1 ) = 0 ), называют |
||
корнем уравнения Pn (z) = 0 .На протяжении многих веков делались попытки получить формулы для вычисления корней уравнений Pn (z) = 0 степени n ³ 3. В 1545 г. итальянский математик, философ и врач Д. Кардано (1501-1576) опубликовал формулы решения кубического уравнения. Возник спор о приоритете с другим итальянским математиком Николло Тарталья (1499-1557). Ученик Кардано Л.Феррари (1522-1565) нашёл способ решения уравнений четвёртой степенипутём сведения к решению кубического уравнения. Норвежский математик Нильс Абель (1802-1829) доказал, что алгебраические уравнения степени n > 4 неразрешимы в радикалах. Это надо понимать в том смысле, что корни уравненияне выражаются через его коэффициенты ak с помощью конечного числаопераций сложения, вычитания, умножения, деления и извлечения корня.
Важный результат о существовании корней алгебраического уравнения носит название основной теоремы алгебры. Эта теорема гласит,
что всякий многочлен Pn (z) степени n ³1 имеет по крайней один ком-
плексный корень. Эта теорема впервые (не вполне строго) была доказана французским учёным Ж. Даламбером (1717-1783).Строгое доказательство дал Карл Гаусс (1777-1855) в 1799 году. Основная теорема алгебры даёт возможность представления многочлена в виде произведения множителей, содержащих его корни
Pn (z) = a0 (z − z1 )(z − z2 )L(z − zn ) ,
откуда следует, что всякое алгебраическое уравнение имеет ровно n корней.
Некоторые из корней могут совпадать. Их называют кратными в отличие от простых, т.е. неповторяющихся корней. Кратность корня – это число его повторений в разложении многочлена на множители. С учётом кратности корней получим разложение многочлена
229
