
9632
.pdf
|
f (x) |
|
|
2 |
|
|
|
|
|
|
cos3x |
|
cos5x |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
4 |
|
cos x |
|
|
9 |
|
|
25 |
|
... |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
sin 2x |
1 |
sin 3x |
1 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
sin x |
2 |
3 |
4 |
sin 4x ... |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
или в компактной записи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
2 |
cos (2k 1)2 |
x |
( 1)n 1 sin nx . |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
k 1 |
|
|
(2k 1) |
|
|
|
n 1 |
|
|
|
|
|
|
|
n |
|
|
|||||||||
Согласно условиям Дирихле в каждой точке непрерывности функции |
|||||||||||||||||||||||||||||||||||
f (x) этот ряд сходится к функции, |
а в точке разрыва даст значение f (x) |
||||||||||||||||||||||||||||||||||
равное 2 (0 ) / 2 |
|
(среднее арифметическое односторонних пределов |
|||||||||||||||||||||||||||||||||
функции в точке разрыва). На рис. 60.4 представлено приближение к |
|||||||||||||||||||||||||||||||||||
рассматриваемой нами функции – «клюшке» сначала в виде суммы |
|||||||||||||||||||||||||||||||||||
следующих гармоник |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
f (x) |
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
sin 2x |
1 |
sin 3x |
|
|||||||||
|
|
|
cos x |
|
|
cos3x |
sin x |
|
|
, |
|||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 60.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а потом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
2 |
|
|
|
|
|
|
1 |
cos3x |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
cos x |
|
|
|
cos5x |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
sin 2x |
1 |
sin 3x |
1 |
sin 4x |
1 |
|
|
|
||||||||||||||||
|
|
|
|
sin x |
2 |
3 |
4 |
5 |
sin 5x . |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

В промежутке ,3 график функции f (x) специально не построен, чтобы
лучше был виден аппроксимирующий её тригонометрический многочлен. При x=0 получаем числовой ряд
|
|
1 |
|
|
|
|
2 |
1 |
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
... , |
|||
|
|
|
2 |
|
8 |
9 |
25 |
|
|||||||||||
|
k 1 (2k 1) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
т.е. ряд Фурье «просуммировал» |
|
числовой ряд. |
Например, при x 2 |
||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1)n 1 |
|
|
|
|
|
( 1)k |
|
|
|
|
1 |
|
1 |
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
... |
|||||
4 |
2k 1 |
|
|
2k 1 |
3 |
5 |
|||||||||||||
k 1 |
|
|
|
k 0 |
|
|
|
|
|
|
|||||||||
60.3. Разложение в ряд Фурье четных функций. Полный ряд Фурье содержит как синусы, так и косинусы. Естественно ожидать, что для чётных или нечётных функций должна пропадать одна из этих составляющих. Наши «надежды» подкрепляются анализом формул для коэффициентов ряда. Пусть f (x) чётная функция, т. е. f ( x) f (x) . Тогда
a |
1 |
|
f (x) dx |
2 |
|
f (x) dx , |
|
|
|
|
|||
|
|
|
|
|||
0 |
|
|
0 |
|
||
|
|
|
||||
что ясно хотя бы из геометрических соображений (см. рис. 60.5).
-π |
|
|
|
|
|
π |
|
|
Рис. 60. 5 |
|
|
|
|
Действительно, в силу чётности функции |
f (x) площади фигур, |
|||||
выражаемые интегралами |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
S1 |
|
f (x) dx , |
S2 |
|
|
f (x) dx , |
|
|
|||||
|
|
|
|
|
0 |
|

равны, поэтому S f (x) dx S1 S2 . Также и коэффициенты an
вычисляются по формулам
a |
1 |
|
f (x) cos nx dx |
2 |
|
f (x) cos nx dx. |
|
|
|
|
|||
|
|
|
|
|||
n |
|
|
0 |
|
||
|
|
|
||||
Последнее равенство следует из предыдущих рассуждений, т.к. подынтегральная функция – чётная. Коэффициенты при синусах обращаются в нули, как интегралы от нечетных функций по промежутку, симметричному относительно начала координат.
Итак, если функция четная, то её ряд Фурье имеет вид
|
a0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (x) |
an cos nx , |
an |
|
f (x) cos nx dx , |
n 0,1,... , |
bn 0 |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
2 |
n 1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример. |
Разложим в ряд Фурье функцию |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
f (x) x2 , x , |
T 2 . |
|
|||||||||||||||||||
Вычисляем коэффициенты ряда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
a |
2 |
x2 dx |
2 |
|
x3 |
|
|
2 2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
3 |
|
|
0 3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
2 |
|
|
2 |
|
2 |
1 |
|
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
an |
|
|
x |
|
cos nx dx |
|
|
|
x |
|
|
|
sin nx |
|
|
|
|
|
x sin nx dx |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
0 |
|
n |
|
|
|
|
||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||
Интегрируя ещё раз «по частям», получаем:
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
an |
|
|
|
|
|
|
x |
|
|
|
cos nx |
|
|
|
|
cos nx dx |
|
|||||||||||||
|
|
|
|
n |
|
n |
n |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
4 |
|
|
cos n |
1 |
|
|
|
|
|
|
|
1 n |
4 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
sin nx |
|
|
|
, |
n 1, 2, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
n2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, |
|
x2 2 |
|
4 |
|
|
|
1 n 1 |
cos nx |
. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полагая в этом равенстве |
x=0 , |
получаем числовой ряд: |
|
|
|||||||||||||||||||||||||||
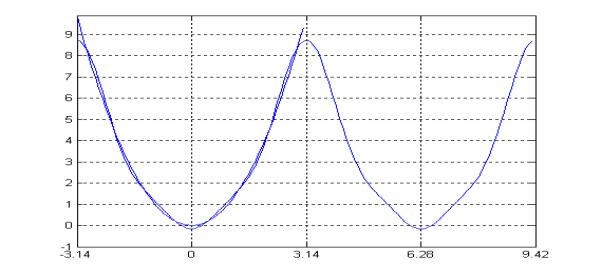
2 |
|
|
|
n 1 1 |
|
|
1 |
|
1 |
1 |
|
1 |
|
1 |
|
|
1 |
|
|
||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
(60.5) |
|||||
12 |
|
|
n2 |
4 |
|
9 |
16 |
25 |
36 |
|
49 |
||||||||||||||||
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
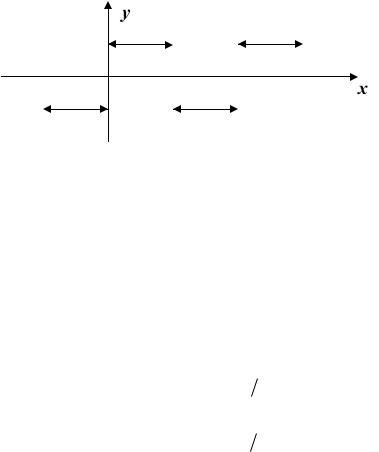
На следующем рисунке представлено приближение функции |
x2 тремя |
||||||||||||||||||||||||||
гармониками |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
||||
|
x |
|
y3 |
|
|
|
4 cos x |
|
|
cos 2x |
|
|
cos3x |
|
|||||||||||||
|
|
|
4 |
9 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис.60.7
Скажем несколько слов о влиянии свойств функции на характер сходимости её ряда Фурье. Мы уже отмечали, что около точек разрыва функции ряд Фурье сходится медленнее, чем в точках непрерывности. Гладкость функции, т.е. её дифференциальные свойства также улучшают сходимость ряда. Когда мы разложили в ряд «клюшку» (см. рис. 60.3), то в
точке её «излома» при x=0 |
получили |
|
|
|
|||||||
2 |
1 |
1 |
|
|
1 |
|
1 |
... |
1 |
... |
(60.6) |
8 |
9 |
25 |
49 |
(2k 1)2 |
|||||||
В этой точке функция непрерывна, но не имеет производной. Подсчитаем число π , взяв одинаковое число членов разложения в рядах (60.5) и (60.6) (пусть п = 7). Во-первых, ряд (60.5) дает возможность оценить ошибку, т.к. он знакочередующийся и ошибка при отбрасывании остатка меньше 1/64 ≈ 0,016. Из ряда (60.6) получаем π ≈ 3,06, а ряд (60.5) дает π ≈
3,16.
Лекция 61. Ряды Фурье (продолжение)
61.1. Разложение в ряд Фурье нечетных функций. Для нечётных функций ряд Фурье имеет вид:
|
|
|
|
|
|
|
|
|
|
|
f (x) bn sin nx , |
|
|
|
|
|
|
|
n 1 |
|
где |
b |
2 |
|
f (x) sin nx dx , |
a 0, |
n 0,1,... |
|
|
|||||
|
|
|||||
|
n |
|
|
|
n |
|
|
|
0 |
|
|
|
|
Коэффициенты при косинусах обращаются в нули, как интегралы от нечетных функций по промежутку, симметричному относительно начала координат.
1, x 0,
Пример. Разложим в ряд Фурье функцию f (x) 0, x 0
1, 0 x
|
1 – |
|
|
|
׀ |
• |
׀ |
׀ |
׀ |
-π |
|
π |
2π |
3π |
–
Рис. 61. 1
b |
2 |
|
sin nx dx |
2 |
|
1 |
cos nx |
|
|
|
|
|
|
||||
|
|
|
|
|
||||
n |
0 |
|
|
|
n |
|
|
|
|
|
|
|
0 |
||||
|
2 |
1 |
0, |
n четное |
|||
|
|
|
|
||||
|
|
|
|
1 cos n 4 |
, n нечетное |
||
|
n |
||||||
|
|
|
n |
||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
4 |
|
sin (2k 1)x |
|
|
|
|||||
Итак, |
|
f (x) |
|
|
|
|
|
|
|
|
или |
||
|
|
|
|
2k 1 |
|
||||||||
|
|
|
|
k 0 |
|
|
|
||||||
|
1 |
|
1 |
|
|
|
1 |
|
4, |
x 0, |
|||
|
|
|
|
|
|
|
|
|
|||||
sin x |
|
sin 3x |
|
|
sin 5x |
|
sin 7x ... 0, |
x 0 |
|||||
3 |
5 |
7 |
|||||||||||
|
|
|
|
|
|
|
4, |
0 x |
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
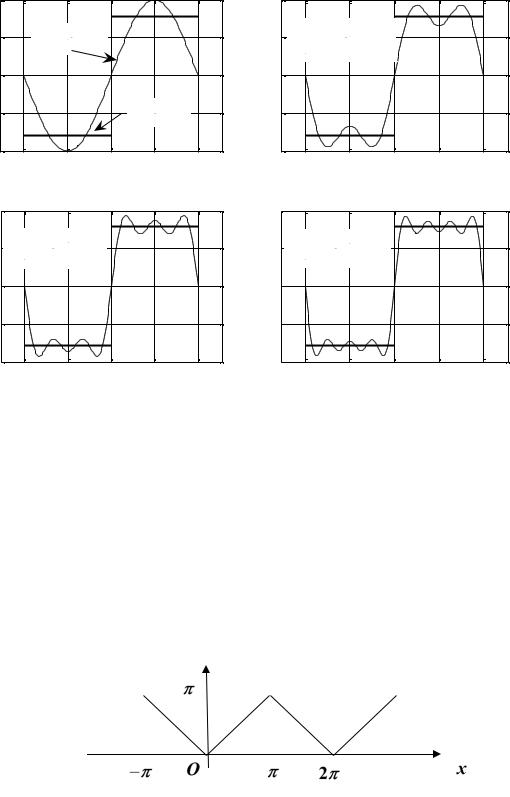
Следующие рисунки показывают, как происходит «приближение» суммы гармоник по мере увеличения их числа к этой кусочно-постоянной функции.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y =sinx |
|
|
|
|
y2=y1+(1/3)sin3x |
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=-pi/4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y3=y2+(1/5)sin5x |
|
|
|
y4=y3+(1/7)sin7x |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
Рис. 61.2 |
|
|
|
|
|
|
61.2. Разложение произвольной функции только по косинусам или |
||||||||||
только по синусам. |
Если в промежутке [-π, π] функция f (x) |
не обладает |
|||||||||
симметрией, т.е. не является ни чётной, ни нечётной, а нужно получить разложение её в ряд Фурье только по косинусам или только по синусам, то такое разложение можно получить в промежутке [0, π ], а на промежуток [- π, 0] продолжить её чётным или нечётным образом.
Пример. |
Разложим в ряд Фурье функцию |
f (x) x, 0 x . |
Продолжим её чётным образом в промежуток [-π;0], |
а затем с промежутка |
|
[-π;π ] на всю ось с периодом Ò 2 (см. рис. 61.3). |
|
|
− |
|
|
|
|
|
|
|
|
|
׀ |
|
׀ |
|
|
|
|
|
|
|
|
Рис.61.3 |
|
|
|
|
|
|||
|
|
2 |
|
2 |
|
x2 |
|
|
|
|
|
|
|
||||||
Вычисляем коэффициенты: a0 |
|
|
x dx |
|
|
|
|
|
|
|
|
2 |
|||||||
|
|
0 |
|
|
0 |
||||
|
|
2 |
|
2 |
x |
|
|
|
1 |
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|||||||||||
a |
|
|
|
x cos nx dx |
|
|
|
sin nx |
|
|
|
|
sin nx dx |
|
|
cos nx |
|
|
|
|
|
n |
n2 |
||||||||||||
n |
|
|
n |
|
|
|
|
|
|
|
|||||||
|
|
0 |
|
|
|
|
0 |
|
0 |
|
|
|
|
0 |
|||
|
2 |
|
cos n |
1 |
|
|
|
|
|
|
0, |
|
n четное |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
n |
2 |
|
|
n |
, n нечетное |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
4 |
|
|
cos |
|
2k 1 x |
|
|
|
|
|
||||||||||
Таким образом, x |
|
|
|
|
|
|
|
|
|
|
|
0 x . |
|
|
|
|||||||||||
2 |
|
|
|
|
2k 1 |
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
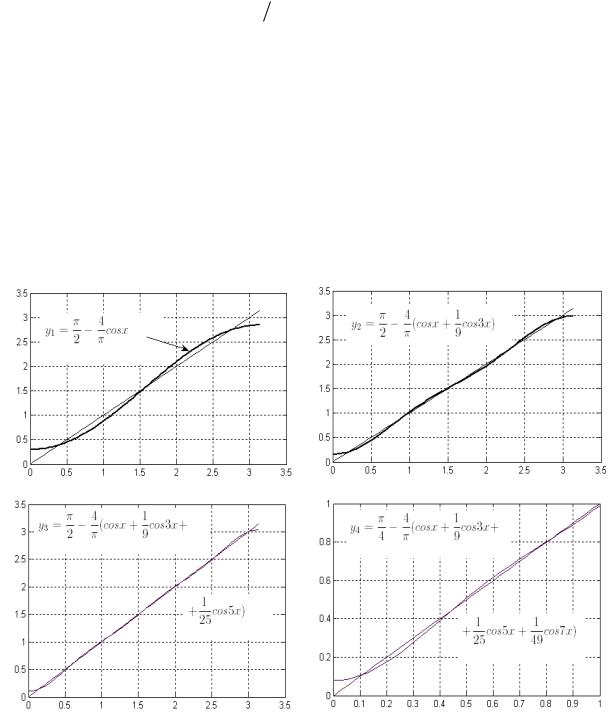
На следующем рисунке приведены графики первых членов ряда Фурье |
||||||||||||||||||||||||||
(п=5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
1 |
|
||
|
|
|
x |
|
|
|
|
|
cos x |
|
|
|
cos 3x |
|
cos 5x |
|
|
cos 7x , |
||||||||
|
|
|
2 |
|
|
9 |
25 |
49 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
последовательно приближающих функцию f (x) x |
в промежутке [0, ] . |
|||||||||||||||||||||||||
Рис. 61.4
Обратите внимание, что на четвёртом рисунке изображён только фрагмент графика, так как в прежнем масштабе графики были бы неразличимы.
Также ещё раз обращаем внимание на тот факт, что там где «раскладываемая» функция недостаточно «хороша» её аппроксимация
отрезками ряда в этих точках «хуже». В нашем случае такая «плохая» точка – начало координат, где функция не имеет производной (см. рис. 61.4)
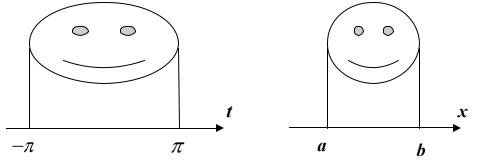
61.3. Разложение в ряд Фурье функции по произвольному промежутку. Предположим, что некоторую функцию f (x) , определенную
в промежутке [a, b], мы хотим представить рядом Фурье. Положение и длина промежутка несущественны, т.к. «сдвигом» и «растяжением» с помощью линейного преобразования
|
a b |
|
b a |
|
|
2 |
|
a b |
|
x |
|
|
|
t ; |
t |
|
x |
|
|
2 |
2 |
b a |
|
||||||
|
|
|
|
|
2 |
||||
Промежуток a ≤ x ≤ b приводится к стандартному промежутку – π ≤ t ≤ π (см. рис. 61.5).
Рис. 61.5
Пусть функция задана в промежутке [- l, l] и имеет период 2l, т.е.
f (x 2l) f (x) . |
|
|
|
|
|
|||
|
|
l |
|
|
|
|
|
|
Несложная замена переменной |
x |
|
t, |
t |
l |
x |
«возвращает» нас к |
|
|
||||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
стандартному случаю. Функция |
f x f |
|
|
t |
как функция переменной t |
|||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
будет иметь период |
T 2 . |
Действительно, |
|
|
|
|
|
|||||||
|
l |
|
|
l |
|
|
|
|
|
l |
|
|
||
f |
|
(t |
2 ) |
f |
|
t 2l |
f |
x |
2l f x f |
|
t |
, |
||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.е., прибавив к аргументу функции число 2π, мы получили то же самое значение функции.
|
l |
|
|
||
Для функции |
f x f |
|
t |
имеем ряд Фурье |
|
|
|||||
|
|
|
|
||

l |
|
|
a |
|
||
|
an cos nt bn sin nt , |
|||||
f |
|
t |
|
0 |
||
|
2 |
|||||
|
|
|
n 1 |
|||
где коэффициенты ряда вычисляются по формулам:
|
|
1 |
|
l |
|
|
1 |
|
|
l |
|
|
|
|
|
|
|
, n 0,1, 2, |
||
an |
|
|
|
f |
|
t cos nt dt , bn |
|
|
|
f |
|
|
t sin nt dt |
|
||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
x |
l |
t |
|
|
|
|
|
|||
«Возвратимся» к старой переменной |
|
|
t |
l |
x |
, тогда ряд примет вид |
||||||||||||||
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a0 |
|
x bn sin n |
x , |
|
f õ |
an cos n |
||||
|
|||||
2 |
n 1 |
l |
l |
||
а коэффициенты после этой несложной замены будут вычисляться по формулам:
1 l |
|
|
1 l |
|
|
|
||||
an |
|
|
f x cos n l |
x dx , |
bn |
|
|
f x sin n l |
x dx, |
n 0,1, |
l |
l |
|||||||||
|
|
l |
|
|
|
|
l |
|
|
|
Раздел 12. Элементы теории множеств, математической логики и теории графов
Лекция 62. Элементы теории множеств
62.1 Общие представления о множествах. Обычно, когда вводится какое-либо новое понятие, то оно опирается на известное понятие или известные понятия, частным случаем которого или которых оно является. Например, параллелограмм есть четырехугольник, у которого противоположные стороны равны и параллельны. Окружность есть линия на плоскости, все точки которой удалены от некоторой фиксированной точки на некоторое фиксированное расстояние и т.д.
Понятие множества является первичным и не имеет формального определения. Один из создателей теории множеств Георг Кантор(18451918) сказал: «Множество есть многое, мыслимое нами как единое». Интуитивно под множеством понимается совокупность различных объектов, объединенных по какому-то одному или нескольким признакам.
Нет никаких ограничений на природу объектов, составляющих множество. Так, про окружность можно сказать, что это множество точек, равноудаленных от фиксированной точки на расстояние радиуса. Можно

говорить о множестве студентов в данной аудитории, о множестве букв некоторого алфавита, о множестве целых числа от 1 до 1000, о множестве атомов серебра в данной монете или о множестве всевозможных идей,
которые имело человечество, и т.д. |
|
|
|
|
Множества часто обозначают прописными |
латинскими |
буквами |
||
A, B,C, X ,Y . Объекты, составляющие множество, называются элементами |
||||
множества и |
обычно обозначаются |
строчными |
латинскими |
буквами |
a, b, c, , x, y . |
Тот факт, что объект |
x принадлежит множеству A , |
||
передается записью x A (читается – «элемент x принадлежит множеству A »). Если x не является элементом A , то пишут x A.
Два множества A и B считаются равными (записывается A B ), если они состоят из одних и тех же элементов. Т.е. A B тогда и только тогда,
когда из того, что x A следует, что x B , а из того, что x B следует, что x A.
Существует два основных способа задания множеств: перечисление и описание. При первом способе просто перечисляются все элементы задаваемого множества. Например, множество букв алфавита некоторого языка определяется списком всех его букв, множество студентов в группе определяется студентами, фамилия и имена которых совпадают со списком в журнале посещаемости, множество простых чисел меньших тысячи может быть задано перечислением всех таких чисел и т.д. В дальнейшем будем пользоваться общепринятыми обозначениями множеств:
N – множество натуральных чисел, Z – множество целых чисел,
Q – множество рациональных чисел,
R – множество действительных чисел, C – множество комплексных чисел.
Конечно, нельзя ни одно из этих множеств (хотя бы в силу их бесконечности) задать перечислением их элементов. Но опыт работы с элементами этих множеств позволяет предполагать, что в каждой конкретной задаче понятно, об элементах каких из перечисленных множеств идет речь.
При втором способе элементы множества задаются при помощи
характеристического свойства, |
устанавливающего, какие |
элементы |
(принадлежащие, как правило, |
некоторому объемлющему |
множеству) |
принадлежат задаваемому множеству. В этом случае в фигурных скобках записывается произвольный элемент множества, а за вертикальной чертой записываются свойства, которыми этот элемент должен обладать:
A x P(x) .
Эта запись означает, что A есть множество таких элементов x , которые обладают свойствами P(x) .
