9632

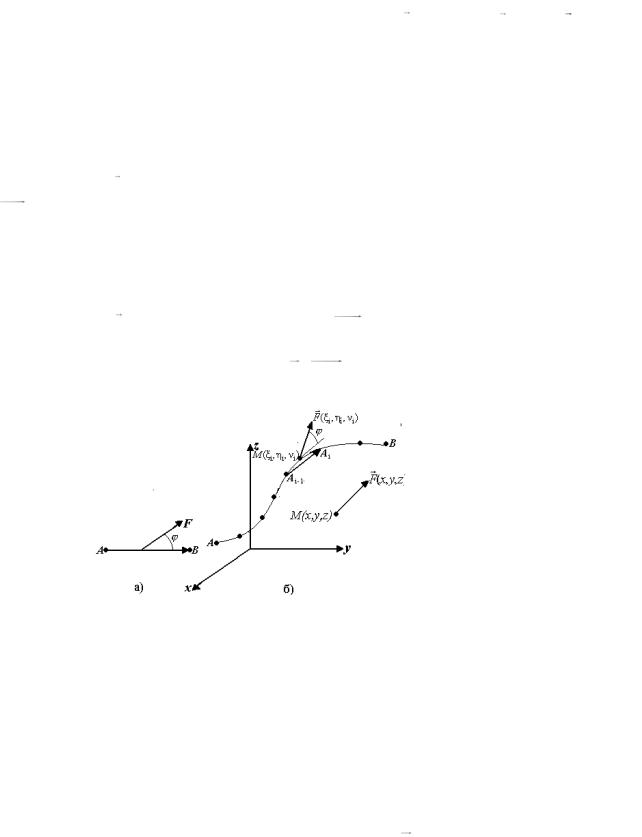
где функции P(x, y, z), Q(x, y, z), R(x, y, z) являются проекциями силы на оси OX ,OY ,OZ соответственно. В случае плоского поля сила задается посредством разложения по единичным векторам F(x, y) P(x, y)i Q(x, y) j . В частности для поля, изображенного на рис. 55.1

Вспомним, что, если при перемещении вдоль отрезка прямой от точки A до точки B сила F постоянна и составляет угол с направлением вектора

Рис. 55.2

Ясно, что в случае криволинейной траектории перемещения и непостоянной по величине и направлению силы, данная формула для подсчета работы неприменима. На помощь, как часто в подобных случаях, приходит интегральная методология. В согласии с ней, для решения поставленной задачи разобьем кривую L на n отрезков (см. рис. 55.2,б). Работа W сил поля по кривой AB очевидно будет равна сумме работ Wi (i 1,..., n) по этим отрезкам кривой. Если считать, что: а) сила поля на

прямой, соединяющему точки Ai 1 и Ai , то согласно формуле (55.1)

вычислено как сумма произведений соответствующих координат этих

Wi P(ξi ηi ,νi ) xi Q(ξi ηi ,νi ) yi R(ξi ηi ,νi ) zi ) .

Втаком случае вся работа сил поля будет приблизительно равна

n

W (P( i , i , i ) xi Q( i , i , i ) yi R( i , i , i ) zi ).

i 1

В качестве точного значения работы W естественно принять предел этой суммы при n и измельчении отрезков, на которые делится кривая L , т.е.

то предел этой суммы при n и li 0 (если он существует и не зависит от способа деления кривой AB и от выбора точек Mi ( i i , i ) ) обозначается, как

f (x, y, z)dx ,

AB

и называется криволинейным интегралом 2-ого рода по координате x от функции f (x, y, z) по кривой AB, т. е.

Если в формуле (55.4) значение функции умножать не на xi , а на yi

или на zi , то мы придем к определению криволинейных интегралов от функции f(x,y,z) по координатам y или z , которые имеют обозначения

Если возвратиться к задаче о вычислении работы сил поля при перемещении материальной точки, то, используя введенные обозначения, формулу (54.2) можно переписать в виде

W P(x, y)dx Q(x, y)dy.

L

55.2. Свойства криволинейных интегралов 2-го рода. В

определении криволинейного интеграла 2-го рода (как и в определениях интегралов других видов) много условий накладывается на факт его существования. Но оказывается, что, если в области D функция f(x,y,z)

непрерывна и кривая L имеет непрерывно изменяющуюся касательную, то криволинейные интегралы (55.4),(55.5) существуют.

Остановимся на свойствах криволинейного интеграла 2-го рода. Непосредственно из определения вытекает, что постоянное число можно выносить за знак криволинейного интеграла и интеграл от суммы или разности равен сумме и разности интегралов. Отметим еще следующие свойства.

1) 1dx x(B) x(A); 1dy y(B) y(A); 1dz z(B) z(A) ,

AB AB AB

где x(B), y (B), z (B) , x(A), y (A), z (A) – абсциссы, ординаты и аппликаты точек A

иB, соответственно.

2)Так как при изменении направления движения по кривой меняется знак приращения координат, то при вычислении криволинейного интеграла 2-го рода, в отличие от криволинейных интегралов 1-го рода, необходимо учитывать направление прохождения кривой AB. И потому:

3) Если точка C разбивает кривую на два участка AC и CB, то

4) Если при перемещении вдоль кривой L от точки A к точке B изменения какой-либо координаты не происходит, то криволинейный интеграл 2-го рода по соответствующей координате равен 0. Это означает,

Применительно к решению задачи о вычислении работы при перемkещении материальной точки в силовом поле этот факт означает, что, если движение по кривой происходит параллельно одной из координатных плоскостей, то проекция силы на ось, перпендикулярную этой плоскости, никакого вклада

вработу не привносит.

55.3.Вычисление криволинейного интеграла 2-го рода.

Вычисление криволинейного интеграла 2-го рода сводится к вычислению определенных интегралов, причем формы сведения существенно зависят от того, в каком виде задана кривая, вдоль которой происходит интегрирование. В случае, когда ситуация рассматривается в пространстве, наиболее естественным является параметрическое задание кривой L, т.е. её определение в виде

P(x, y,z)dx Q(x, y,z)dy R(x, y,z)dz

Вычислим, например, криволинейный интеграл

xdx ydy+(x+y 1 )dz

L

где кривая L есть отрезок прямой, соединяющий две точки A(1, 1,1) и

. Для этого запишем уравнение прямой, проходящей через точки

A и B в параметрическом виде:

x t 1, y 2t 1, z 3t 1 0 t 1.

то в первом случае переменную x можно считать параметром, а во втором случае переменную y можно считать параметром и формула (55.8) примет

вид

прямой.

Рис. 55.3

Этот простой пример показывает, что значение криволинейного интеграла 2-го рода существенно зависит от того, по какой кривой происходит перемещение из одной точки в другую.

55.4. Криволинейный интеграл по замкнутому контуру. Формула Грина. В физических задачах нередко возникают ситуации, когда кривая L, по которой происходит перемещение, представляет собой замкнутый контур, т.е. она является замкнутой и не пересекает сама себя (см.рис.55.4). Криволинейный интеграл 2-го рода, вычисляемый по такой кривой, называется криволинейным интегралом по замкнутому контуру, и он имеет специальное обозначение

В этих обозначениях не видна начальная точка A . Но из 3-го свойства криволинейных интегралов следует, что криволинейные интегралы (2.13) не зависят от положения начальной точки на контуре L, а зависят лишь от направления обхода контура L.

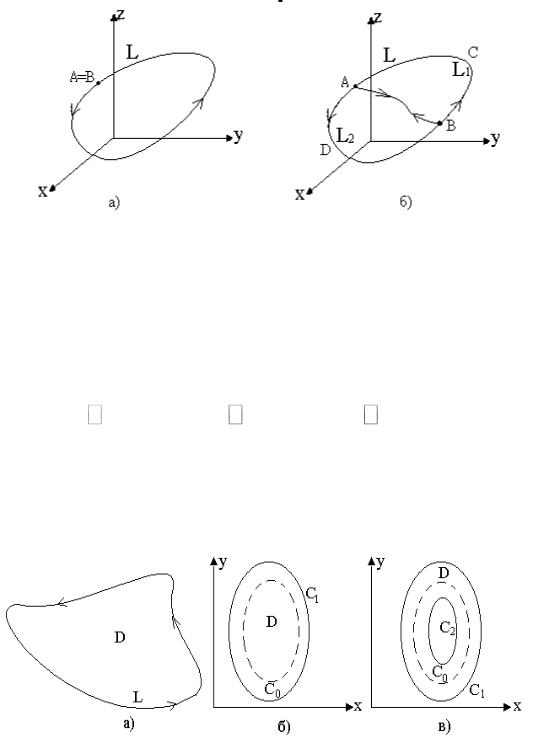
Рис. 55.4

Если на контуре L отметить две точки А и В и соединить их некоторой кривой АВ, то сформируются два контура: контур L1 , проходимый в последовательности АВСА и контур L2 , проходимый в последовательности ADBA. В таком случае будет справедлива формула

Сосредоточим внимание на случае, когда замкнутый контур L лежит на плоскости. Будем говорить, что этот контур обходится в положительном направлении, если ограниченная этим контуром область на плоскости остается слева от направления обхода.

Рис. 55.5

На рис. 55.5,а) контур L обходится в положительном направлении, т.к. область D, ограниченная этим контуром, остается слева от направления обхода. Замкнутая область D на плоскости называется односвязной, если любой замкнутый контур, лежащий в области D, можно непрерывно стянуть в точку, не выходя за пределы области D. Области, изображенные на рис. 55,а и рис. 55.5,б являются односвязными, а область D изображенная

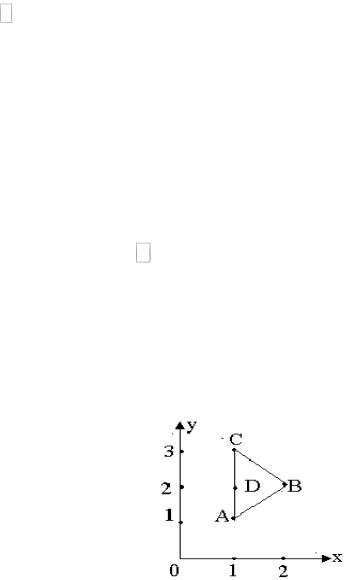
на рис. 55.6,в , ограниченная извне контуром C1 , а изнутри контуром C2 таковой не является, т.к. контур C0 нельзя стянуть в точку, не выходя за

пределы области D.

Небольшой экскурс в область свойств и способов обхода замкнутых кривых на плоскости объясняется тем, что английский математик Джордж Грин доказал следующую теорему, которая устанавливает, на первый взгляд, несколько неожиданную связь между криволинейными интегралами по замкнутому контуру и двойными интегралами.

Теорема. Пусть функции P(x, y), Q (x, y) , Py (x, y),Qx (x, y) непрерывны в односвязной области D, ограниченной контуром L , который имеет непрерывно меняющуюся касательную. Тогда справедлива следующая формула («Формула Грина»)

где контур L обходится в положительном направлении.

Иными словами, формула Грина позволяет вычисление криволинейного интеграла по замкнутому контуру свести к вычислению двойного интеграла по области, ограниченной этим замкнутым контуром. Поверив без доказательства в справедливость приведенной формулы, применим ее, например, для вычисления следующего криволинейного интеграла:

(x2 y2 )dx (x y)2 dy ,

L

где L – контур треугольника с вершинами в точках A(1,1), B(2,2), C(1,3) ,

Рис. 55.6

Применив формулу Грина (55.12), получаем

(x2 y2 )dx (x y)2 dy ( 2(x y) - 4 y )dxdy 2(x - y)dxdy

Если в формуле (55.12)поменять местами левую и правую части, то можно будет увидеть, что формула Грина является обобщением формулы Ньютона–Лейбница. Действительно, по формуле Ньютона–Лейбница значение определенного интеграла по внутренности отрезка равно разности значений первообразной на концах отрезка. Также и формула Грина показывает, что значение двойного интеграла от функции, определенной во внутренности области D может быть вычислено с помощью криволинейного интеграла от функций, определенных только на границе этой области.

Воспользуемся формулой Грина для определения работы сил поля F (x, y) x2 yi xy2 j при перемещении материальной точки вдоль

окружности L с уравнением x2 y2 a2 . Работа W в данном силовом поле будет определяться по формуле W (- x2 y) dx + xy2dy . Так как в нашем

Лекция 56. Независимость криволинейного интеграла 2-го рода от пути интегрирования

В предыдущей лекции было обращено внимание на тот факт, что криволинейный интеграл 2-го рода зависит в общем случае не только от положения начальной и конечной точек на плоскости или в пространстве, но и от кривых, по которым происходит процесс интегрирования. В то же время, из курса физики известно, что в поле силы тяжести или в электростатическом поле работа сил поля по перемещению тела или заряда из одного положения в другое не зависит от пути, по которому это перемещение происходит. Также известно, что для каждого из упомянутых силовых полей существует так называемая потенциальная функция. Это означает, что с каждой точкой пространства удается связать некоторое число, называемое потенциалом, и работа сил поля по перемещению объекта из одного положения в другое определяется как разность потенциалов в конечной и начальной точках перемещения. Ранее было установлено, что работа сил поля вычисляется с помощью криволинейных интегралов 2-го рода. В связи с этим естественно возникает вопрос: «при каких условиях криволинейные интегралы 2-го рода не зависят от пути интегрировании?» или в физической интерпретации: «когда исследуемые физические силовые поля обладают вышеуказанными свойствами?». В этой лекции будет дан исчерпывающий ответ на данный вопрос.

56.1. Случай плоского силового поля. Остановимся на случае плоского силового поля, т.е. на рассмотрении криволинейного интеграл

P(x,y)dx Q(x,y)dy .

AB

Следующая теорема показывает, что многие свойства силовых полей очень тесно взаимосвязаны и вытекают одно из другого.

Теорема. Если функции P(x, y), Q(x, y), Py (x, y), Qx (x, y)

непрерывны в односвязной области D на плоскости, то следующие четыре утверждения эквивалентны:

1) По любому замкнутому контуру L , целиком лежащему в области D, выполняется равенство: