
9624
.pdf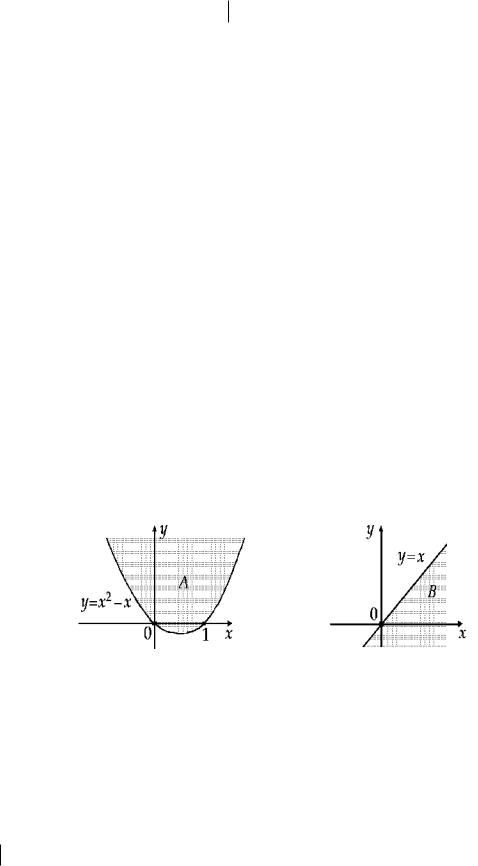
Свойства P(x) могут быть заданы или в виде словесного описания,
или в виде неравенств, или в виде уравнений. Например, множество натуральных чисел от 1 до 1000 может быть записано таким образом:
N1000 x x N и x 1000 .
Множество, записанное следующим образом:
|
|
|
|
|
|
|
||
|
|
n N и уравнение x |
n |
y |
n |
z |
n |
|
Ф n |
|
|
|
|
имеет решение в целых числах |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
связано с великой теоремой Ферма.
Однако состав множества, определенного описанием, не всегда очевиден, и причина этого кроется гораздо глубже, чем просто недостаточная выразительность языка. Так, только недавно было доказано (доказана теорема), что приведенное выше множество Ф состоит всего из двух элементов: Ф ={1,2}.
Если множество A содержит конечное число элементов, то говорят,
что оно конечно, в противном случае |
множество A называется |
||||||||||||||||
бесконечным. Если множество A конечное, то |
|
A |
|
будет означать число |
|||||||||||||
|
|
||||||||||||||||
элементов в |
A . |
|
Приведенные множества |
N1000 |
|
и Ф конечные, причем |
|||||||||||
|
N1000 |
|
1000 |
и |
|
Ф |
|
2 , а описанные множества пар чисел |
|||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
A (x, y) |
|
y x2 x и |
B (x, y) |
|
y x , |
|||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
геометрические интерпретации которых приведены на рис. 62.1, являются бесконечными.
Рис. 62.1
Само слово «множество» наводит на мысль, что в множестве содержится много элементов. Но это не так. Можно рассматривать множества, состоящие всего из одного элемента, и даже множество, не имеющее ни одного элемента. Последнее множество называется пустым множеством и для него существует обозначение: . Например, множество
A x x N и для любого натурального числа y N, что xy y

состоит всего из одного элемента, которым является 1, а множество
|
|
|
B x |
x N и x2 |
1 0 |
|
|
|
не содержит элементов и, следовательно, B = .
Все пустые множества равны между собой, иначе говоря, существует только одно пустое множество.
62.2. Подмножества. Универсальное множество. Множество всех подмножеств данного множества. Понятие подмножества возникает тогда, когда необходимо рассматривать некоторое множество не самостоятельно, а как часть другого, более широкого множества.
Множество |
B называется подмножеством множества A (записывается |
B A ), если всякий элемент множества B является элементом множества A |
|
. Запись B A не исключает, что A B . |
|
Пустое множество является подмножеством любого множества. Из |
|
определения |
следует, что любое множество является подмножеством |
самого себя: |
A A . Таким образом, у каждого множества (кроме пустого) |
есть, по крайней мере, два подмножества – само множество и пустое множество. Нетрудно проверить следующее свойство: из того, что A B , а B C следует, что A C . В самом деле, будем рассуждать от противного. Пусть A B и B C , но A C и A C . Тогда существует такой элемент, что a A, но a C . Но так как B C , то a B . Получили противоречие: a A, a B, но A B .
Если все рассматриваемые в ходе рассуждений множества являются подмножествами некоторого фиксированного множество U , то это множество называют универсальным множеством или универсом для рассматриваемого набора множеств.
Истинным, строгим или собственным подмножеством множества A
называется такое его подмножество B , что B A и B A (записывается |
|
B A ), где – знак строгого включения. По отношению к множеству A |
|
пустое множество и само множество A |
называются несобственными |
подмножествами множества A . |
|
Рассмотрим следующие три множества |
A = {0, 1}, B = {{0, 1},2} и |
C = {{{0, 1},2},3}. Обратим здесь внимание на следующий факт: A B (т.к. множество A является элементом множества B ), B C (т.к. множество B является элементом множества C ), но A C (т.к. множество A не является элементом множества C ). Но множество A не является подмножеством множества B (т.к. 0 A но 0 B ) и множество B не является подмножеством множества C (т.к. 2 B , но 2 C ).
Рассмотрим множество A a,b,c . Для этого множества A 3 . Найдем
все его различные подмножества. Таковыми будут: пустое множество Ø, три одноэлементных подмножества a, , b , c , три двухэлементных

подмножества a,b , a,c , b,c и одно трёхэлементное множество a,b,c (само множество A). Т.е. существует всего 8 подмножеств этого множества.
Для произвольного множества A множество всех его подмножеств
называется булеаном множества A и обозначается как или 2 A .
Последнее обозначение происходит из того факта, что для конечного множества A a1,a2,…,ak , состоящего из k элементов
S( A) 2 A .
Действительно, для k=1,2 в этом легко убедиться. Для k=3 нас убеждает равенство 8=23. Теперь будем рассуждать по индукции. Допустим данное равенство справедливо для множества A a1,a2,…,ak , состоящего из k
элементов. Покажем его справедливость для множества A1 a1,a2,…,ak , ak 1 , состоящего из (k+1) элемента. Существует ровно
2k подмножеств этого множества, которые не содержат элемента
Если к каждому из таких подмножеств добавить элемент ak 1 , то получим все подмножества, содержащие элемент ak+1. Таким образом,
S(A1) 2k 2k 2k 1 ,
и, следовательно, приведенное равенство справедливо при любом значении k.
62.3. Алгебраические операции над множествами. Операции над множествами позволяют из имеющегося набора множеств получать другие множества. Наиболее употребительными являются следующие операции.
Объединением множеств A и B называется множество, обозначаемое A B , содержащее в себе как элементы множества A , так и элементы множества B .
Пересечением множеств A и B называется множество, обозначаемое A B , состоящее из элементов, входящих одновременно в A и в B .
Разностью множеств A и B называется множество, обозначаемое A \ B , состоящее из элементов множества A , не входящих в множество B .
Симметрической разностью множеств A и B называется множество
A B (A \ B) (B \ A) .
Дополнением множества A до универсума U называется множество
A U \ A.
На рис. 62. |
2,а приведены два множества A и B . На рис. |
62.2,б-62.2,е |
заштрихованы результаты соответствующих |
операций над этими множествами. На рис. 62.2ж - 62.2з приведено множество А и его дополнение до универсума U .
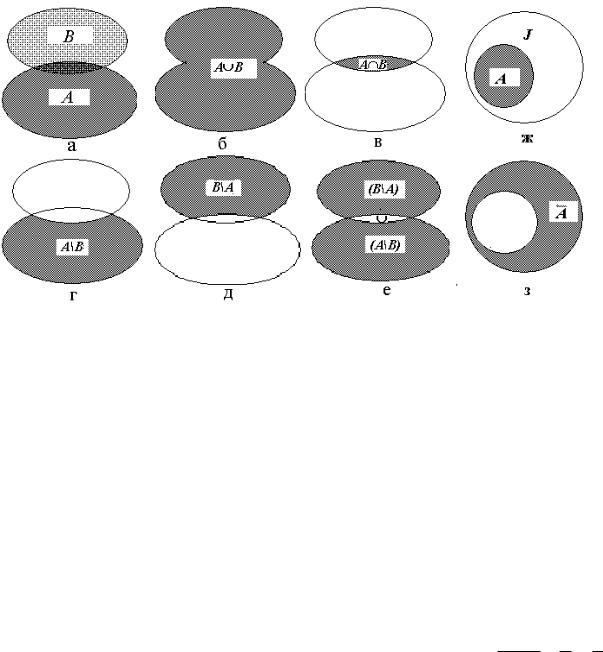
Рис. 62.2
Если A B =Ø, то говорят, что множества A и B не пересекаются. Между введенными операциями существуют определенные
взаимозависимости, которые называются |
законами алгебры множеств. |
|||||||||||
Среди таковых выделяются так называемые законы де Моргана |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A B A B и |
A B A B |
||||||||||
и свойства дистрибутивности пересечения относительно объединения и объединения относительно пересечения:
A (B С) (A B) (A С) и A (B С) (A B) (A С) .
Все эти законы, а также другие соотношения в алгебре множеств могут быть установлены с помощью поэлементной схемы доказательства, заключающейся в проверке принадлежности элементов множеств, стоящих в левой части равенств множествам, стоящим в правой част и, и наоборот. Проверим, например, первое равенство де Моргана: A B A B
. Операция дополнения предполагает наличие некоторого
универсума U . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Итак, пусть x A B. |
Это означает, что x U и |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x A B . |
Но в |
таком случае x A |
и |
x B и, следовательно, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
x A B . |
Предположим теперь, что |
x A B . Это означает, что |
|||||||||||||||
|
|
|
|
|
|
|
|
x A и x B и, |
||||||
x U , а также x A |
и x B . Отсюда следует, что |
|||||||||||||
|
x A B . |
|
|
|
|
|
|
|
|
|
||||
значит, |
|
|
|
Но т.к. x U , то x A B . |
|
|
|
|||||||
Если множество X |
является объединением нескольких множеств, т.е. |
|||||||||||||
|
|
, |
то говорят, что |
множества A , A ,…,A |
образуют |
|||||||||
X A A …, A |
|
|
|
|
1 2 |
n |
|
|
||||||
1 |
2 |
n |
|
|
|
|
|
|
||||||
покрытие множества |
|
X . Если при |
этом все множества A , A ,…,A |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
n |
попарно не пересекаются, то эта система множеств называется разбиением множества X .
Пусть, например, X ={1,2,3,4,5.6,7,8}. Система множеств
A1 ={1,3,4,6,7,8}, A2 ={1,5,8}, A3 ={1,2,3,4} образует покрытие множества
X , а система множеств |
B1 ={1,3,6,7}, B2 ={5,8}, B3 ={2,4} образует |
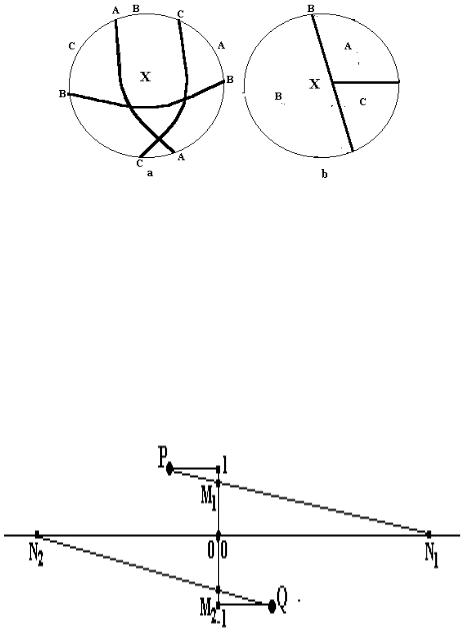
разбиение множества X . На рис. 62.3,а система областей, ограниченных |
|
контурами AAA , BBB , |
CCC , образуют покрытие множества X , а на |
рис. 63.2,b области A, B,C образуют разбиение множества X .
Рис. 62.3
62.4. Эквивалентность множеств. Мощность множеств. Множества
A и B . называются эквивалентными, если между их элементами можно
установить взаимно однозначное соответствие. Если имеются два конечных |
|||||||||
|
1 2 |
k |
|
|
|
|
|
|
|
множества |
A a ,a |
,…,a |
и |
B b ,b ,…,b |
|
,состоящие из |
|||
|
|
|
|
1 2 |
k |
|
|||
|
|
|
|
|
|
|
|
||
одинакового количества |
элементов, то, поставив в соответствие элементу |
||||||||
ai (i=1,2,…,k) из множества A элемент bi из множества B , мы тем самым
устанавливаем взаимно однозначное соответствие между этими множествами. Таким образом, любые два конечных множества, содержащие одинаковое количество элементов, эквивалентны.
Рис. 62.4
На рис. 62.4 установлено взаимно однозначное соответствие между точками числового интервала (-1,1) (он нарисован вертикально ) и точками числовой прямой (- ,+ ). Числу 0 из интервала (-1,1) соответствует число 0 на прямой (- ,+ ). Положительному числу x1 интервала (-1,1)

соответствует положительное число y1 на прямой (- ,+ ). Отрицательному числу x2 интервала (-1,1) соответствует отрицательное число y2 на прямой (- ,+ ). Таким образом, множество чисел на интервале (-1,1) эквивалентно множеству чисел на прямой (- ,+ ).
Под мощностью множества естественно подразумевать количество содержащихся в нем элементов и потому мощность конечного множества A определяется как A . Из сказанного выше, например, следует, что
мощность булеана множества A a1,a2,…,ak равна 2k .
Для бесконечных множеств понятие мощности опирается на понятие
эквивалентности |
множеств. Естественно считать два эквивалентных |
множества равномощными. Также естественно считать, что если B A , |
|
то мощность |
множества B меньше или равна мощности A . |
Вышеприведенный пример показывает, что множество чисел на интервале (-1,1) равномощно множеству чисел на прямой (- ,+ ).
Говоря, что множество бесконечно, мы имеем в виду, что из него можно взять элемент, два элемента и т.д., причем после каждого такого шага в этом множестве ещё останутся элементы. «Простейшим» среди бесконечных множеств является множество натуральных чисел. Счетным множеством называется всякое множество эквивалентное множеству натуральных чисел N . Иначе говоря, элементы счетного множества A можно перенумеровать натуральными числами или, что то же самое, можно
представить в виде последовательности a1,a2 ,…,ak .....
Множество целых чисел Z является счетным, ибо все целые числа мы можем расположить в виде такой последовательности:
0,1,(-1),2,(-2),…
Нетрудно также понять, что счетными множествами являются множество всех четных положительных (отрицательных) чисел или множество натуральных степеней числа 2. Не так очевиден тот факт, что
множество всех рациональных чисел Q также является счетным.
Создатель теории множеств Георг Кантор показал, что мощность булеана любого множества A больше мощности множества A . И таким образом, не существует множества наибольшей мощности. Можно показать, что множество действительных чисел на отрезке (-1,1)
эквивалентно булеану множества натуральных чисел и потому не является счетным. Оно называется множеством мощности континуум. Из вышесказанного следует, что множество чисел на всей числовой прямой также является множеством мощности континуум. Такой же мощностью обладают множества точек плоскости или трехмерного пространства.
62.5. |
Прямое произведение множеств. |
Прямым |
||
(декартовым) произведением множеств |
A и |
B |
называется |
|
|
A B (a, b) a A, b B |
|
|
|
множество |
, |
т.е. |
множество тех и |
|
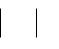
только тех пар, первый элемент которых принадлежит множеству A , а второй множеству B .
Если, к примеру,
A a, b, c, d, e, f , g, h , а B ={1,2,3,4,5.6,7,8},
то A B совпадает с нумерацией клеток на шахматной доске. Введем обозначения:
A2 A A, An A A .... A .
Множество A2 называется декартовым квадратом множества A , а множество An называется n-ой декартовой степенью множества A . Если вспомнить, что R есть множество действительных чисел, то множество R2 (x, y) x R, y R эквивалентно множеству точек на плоскости. Это понимается таким образом, что если на плоскости введена декартова система координат, то паре (x, y) R2 ставится взаимно однозначно точка
M , имеющая координаты (x, y) . Точно так же R3 эквивалентно
множеству точек в трехмерном пространстве с введенной декартовой системой координат.
Очевидно, что для конечного множества A верно равенство:
An A
A n
n
62.6. Бинарные отношения. Отношение эквивалентности. Пусть имеется множество A . Любое подмножество G A A называется бинарным отношением, определенным на множестве A . Т.е. бинарное отношение G есть некоторая совокупность пар (x, y) из элементов
множества A .
Если задано бинарное отношение G и (x, y) G , то говорят, что x и y находятся в отношении G и записывают так: xGy . Примером бинарного отношения на множестве действительных чисел является отношение « x y ». Его можно рассматривать как подмножество тех пар
(x, y) из множества R R , в которых первое число меньше второго или
равно второму числу.
Пусть N есть множество натуральных чисел. Будем считать, что xGy , если x и y при делении на 5 дают один и тот же остаток. Обычно это записывается так x y(mod 5) . Например, 5=35 (mod 5), но 5≠34 (mod 5)
.
Бинарные отношения на множестве A могут обладать или не обладать следующими свойствами.
1) Бинарное отношение G |
называется рефлексивным, если для |
любого x A справедливо, что |
xGx . |
2)Бинарное отношение G называется симметричным, если из того, что xGy следует, что yGx .
3)Бинарное отношение называется транзитивным, если из того, что xGy и yGz следует, что xGz .
Очевидно, |
что |
отношение |
« x y » |
является |
рефлексивным |
и |
|
транзитивным, |
но |
не является |
симметричным. |
А вот |
отношение |
||
x y(mod 5) обладает всеми перечисленными выше свойствами. |
|
||||||
Бинарное |
отношение G |
на |
A называется |
отношением |
|||
эквивалентности, если оно рефлексивно, симметрично и транзитивно. |
Из |
||||||
приведенного определения следует, что отношение x y(mod 5) является отношением эквивалентности, а отношение « x y » таковым не является.
Рис. 62.5
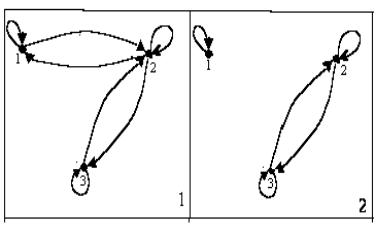
На рис. 62.5 представлены 2 графа с тремя вершинами. Будем считать, что вершина с номером i находится в отношении G к вершине с номером j, если они соединены дугой. Нетрудно видеть, на втором графе отношение G является отношением эквивалентности, а на первом графе отношение G не является отношением эквивалентности, т.к. не выполняется свойство транзитивности: имеем дугу из вершины 1 в вершину 2, дугу из вершины 2 в вершину 3, но отсутствует дуга из вершины 1 в вершину 3.
Пусть A есть множество точек на плоскости с введенной на ней
декартовой системой координат OXY |
и пусть точка |
P(x ,y ) и точка |
||
|
|
1 |
1 |
1 |
P2 (x2 ,y2 ) находятся в отношении D друг к другу, если они находятся на одном и том же расстоянии от прямой 2x 3y 6 . Очевидно, отношение
D есть отношение эквивалентности.
Пусть на множестве A задано отношение эквивалентности G и а есть некоторый элемент из A . Пусть С(a) есть подмножество элементов из A ,
эквивалентных элементу а. Если множество A\ С(a) не пусто, то выберем из него элемент b и образуем подмножество С(b) элементов из
A , эквивалентных элементу b и т.д. до тех пор, пока в оставшейся части множества A не останется ни одного элемента. Полученная система подмножеств является разбиением множества A и называется системой классов эквивалентности бинарного отношения G .
Например, введенное выше отношение x y(mod 5) разбивает все
множество натуральных чисел на 5 классов эквивалентности. Отношение эквивалентности G , определенное вторым графом на рис. 62.5, разбивает вершины графа на два подмножества: {1} и {2.3}.
Классом эквивалентности отношения D , веденного выше на плоскости, является любая прямая, параллельная прямой 2x 3y 6 , и,
следовательно, плоскость разбивается на бесконечное число классов эквивалентности.
Пусть A множество студентов некоторой группы. Будем считать, что студент x находится в отношении G к студенту y , если они имеют одну
и ту же словесную оценку за экзамен по математике в прошедшей сессии. Очевидно, отношение G есть отношение эквивалентности, и все множество студентов разбивается не более, чем на 4 класса эквивалентности. Если все студенты сдали экзамен на отлично, то вся группа состоит из одного класса эквивалентности.
Лекция 63. Элементы математической логики
63.1. Введение. Согласно одному из определений, логика есть анализ методов рассуждений. Изучая эти методы, логика в первую очередь интересуется формой, а не содержанием доводов в том или ином рассуждении. Иначе говоря, логика интересуется лишь одним аспектом рассуждений, а именно, правильно ли делается вывод (заключение) из предварительно проведенных рассуждений, т.е. вытекает ли истинность заключения данного рассуждения из истинности его посылок. Рассмотрим два примера.
1.Все натуральные числа, сумма цифр которых в десятичной записи делится на 9, делятся на 9. Число а делится на 9, следовательно, сумма его цифр делится 9.
2.Все мужчины, пришедшие на презентацию, в красных галстуках. Гоcподин Х в красном галстуке. Следовательно, он пришел на презентацию.
Несмотря на схожесть рассуждений, в первом рассуждении сделанное заключение истинно, а во втором рассуждении сделанное заключение не является истинным.
Математическая логика занимается изучением математических рассуждений. Главная ее цель дать точное и адекватное определение
понятия «математическое доказательство». Особый интерес к логике и, прежде всего математической, проявился, когда были открыты парадоксы, т.е. рассуждения, приводящие к противоречиям.
Парадокс лжеца. Некто говорит «Я лгу». Если при этом он лжет, то сказанное им есть ложь и он не лжет. Если же он при этом не лжет, то сказанное им есть истина, и, следовательно, он лжет. В любом случае оказывается ,что он лжет и не лжет одновременно.
Парадокс Бери 1906г. Некоторые фразы русского языка выделяют вполне конкретные натуральные числа. Например, фраза: «Наименьшее четное число» выделяет число 2». Эта фраза содержит менее 50 слогов. Существует лишь конечное число слогов в русском языке. Следовательно, существует лишь конечное число таких фраз русского языка, которые содержат не более пятидесяти слогов. Поэтому с помощью таких фраз можно охарактеризовать только конечное число натуральных чисел. Пусть
K есть наименьшее из натуральных чисел, которые нельзя
охарактеризовать никакой фразой русского языка, которая содержит не более 50 слогов. Но нетрудно видеть, что сама эта фраза, которая характеризует число K , содержит менее 50 слогов.
Анализ парадоксов привел к различным планам их устранения. Углубилось исследование языка логики и математики и в результате на стыке логики и математики возникло целое научное направление: «математическая логика». С самыми элементарными понятиями математической логики нам предстоит познакомиться в данной лекции.
63.2. Высказывания. Алгебра высказываний. В математической логике основными неопределяемыми являются следующие понятия: высказывание, истина, ложь. Под высказыванием понимается любое повествовательное предложение, относительно которого можно сказать истинно оно или ложно. Например, высказывание «Студент, сдавший экзаменационную сессию на «отлично», получает повышенную стипендию» есть истинное высказывание; а высказывание «Число 6 делится на 4» есть ложное высказывание.
Пропозициональными переменными, обозначаемыми заглавными латинскими буквами А,В,С,…, будем называть переменные, значениями которых являются произвольные высказывания (истинные или ложные). К высказываниям можно применять те или иные операции. В результате появляются новые высказывания, истинностные значения которых зависят от истинностных значений высказываний, к которым операция применена. Приведем определения наиболее употребительных операций над
высказываниями. |
|
|
|
|
|
Отрицанием |
высказывания |
А |
называется высказывание, |
||
|
|
|
|
|
|
записываемое в виде |
|
A (читается: "не А "), |
которое истинно, если А ложно, |
||
и ложно, если А истинно. Это отражено в таблице истинности 1: таб.1
