
9624
.pdf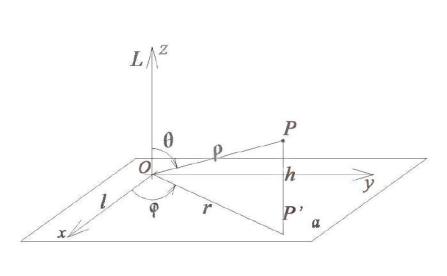
Лекция 53. Тройной интеграл в сферических координатах. Приложения к механике
53.1. Вычисление тройного интеграла в сферических координатах.
Чтобы ввести сферические координаты в трёхмерном пространстве, рассмотрим снова плоскость α и перпендикулярную ей ось L . На плоскости α введём ось l . Тогда сферические координаты ( , , ) точки P будут представлять собой соответственно её расстояние от начала координат (длина радиус–вектора точки P ), угол между проекцией OP
радиус-вектора точки P на плоскость α и осью l , а также угол θ между радиус-вектором OP и осью L (рис. 53.1). Координатная поверхность ρ const является сферой, что объясняет название координат.
Для описания всех точек в пространстве достаточно следующих промежутков изменения координат: 0 ρ , 0 θ π, 0 2π .
Введём декартову систему координат, совместив ось Ox с осью l , а плоскость xOу декартовой системы – с плоскостью α (рис. 53.1).
Декартовы координаты точки P обозначим (x, y, z) , тогда координаты её проекции P на плоскость xOу приобретут значения (x, y,0) . Поскольку расстояние r OP и угол являются полярными координатами точки P
, то x r cos , y r sin .
|
Рис. 53.1 |
|
Учитывая, что OP ρsinθ |
и z ρcosθ , получим связь сферических и |
|
декартовых координат в виде |
|
|
x ρ sin θ cos |
|
|
|
|
|
y ρ sin θ sin |
(53.1) |
|
|
|
|
ρ cos θ |
|
|
z |
|
|
Пусть для примера поверхность задана в декартовых координатах уравнением
x2 y2 z2 2 a2 x2 y2 .
По такому уравнению представить вид поверхности весьма непросто. Перейдём к сферическим координатам, пользуясь соотношениями (53.1)
|
ρ |
2 |
sin |
2 |
θcos |
2 |
2 |
sin |
2 |
sin |
2 |
2 |
cos |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 2 sin2 cos2 2 sin2 sin2 .
После очевидных преобразований уравнение упрощается
4 sin2 cos2 2 a2 2 sin2 ,
что дает ρ2 a2 sin2 θ или, окончательно, ρ a sin θ .
Теперь можно представить вид поверхности. Во-первых, ясно, что она имеет одинаковые сечения плоскостями const . Во-вторых, можно определить вид этих сечений. Для этого перейдём в плоскости yOz к
декартовым координатам по формулам, которые получаются из (53.1), если
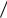 2
2
z cos
y sin .
Уравнение сечения рассмотрим в виде 2 a sin , что дает в координатах
( y, z) уравнение y2 z2 ay |
или после выделения полного квадрата |
|||||
|
|
a |
2 |
a |
2 |
|
y |
|
|
z2 |
|
. |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
||
Видим, что сечение это является окружностью радиуса a2 .
Пришли к тому, что исходная поверхность представляет собой тор, т.е. закрученную вокруг оси Oz окружность, закрепленную в начале координат (половина поверхности изображена на рисунке 53.2).
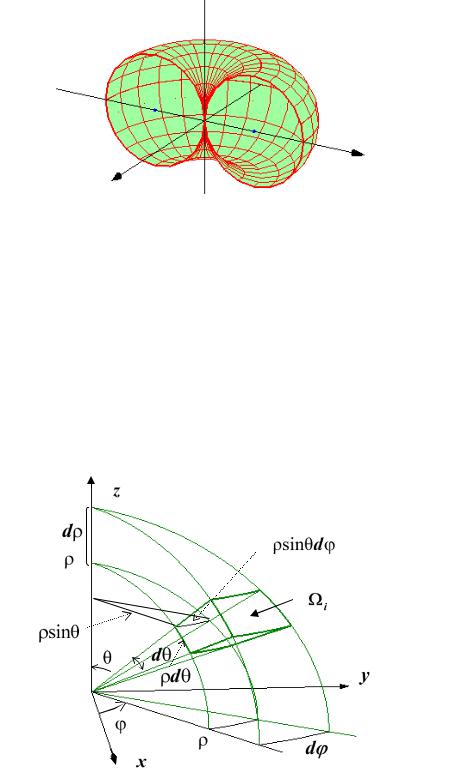
Рис.53.2
Чтобы найти элементы объёма в сферических координатах, построим поверхности семейств ρ const (сферы), θ const (конические поверхности с вершиной в начале координат) и const (полуплоскости, проходящие через ось Oz ). Рассмотрим один из элементов i ,
ограниченный сферами радиусов ρ |
и ρ dρ , конусами растворов θ и |
θ dθ , а также полуплоскостями, |
проведёнными через ось Oz , следы |
которых в плоскости xOу имеют полярные лучи и d (рис. 53.3).
Рис. 53.3
Представив подобласть i как прямоугольный параллелепипед со сторонами dρ , ρ dθ и ρsinθd , получим элементарный объём в виде
dV ρ2 sin θ dρd dθ . Поэтому формула перехода в тройном интеграле от декартовых координат к сферическим приобретает вид
f (x, y, z)dxdydz f (ρsinθcos ,ρsinθsin ,ρcosθ)ρ2sinθdρd dθ . |
|
|
|
Итак, при переходе в тройном интеграле от декартовых к сферическим координатам подынтегральная функция должна быть выражена через
переменные ρ , и θ по формулам (53.1), а также умножена на ρ2 sinθ .
Сферические координаты используем для нахождения |
объёма тела |
|||
, ограниченного |
сферой x2 y2 z2 2az |
и двумя |
коническими |
|
поверхностями |
x2 y2 z2tg2α и |
x2 y2 |
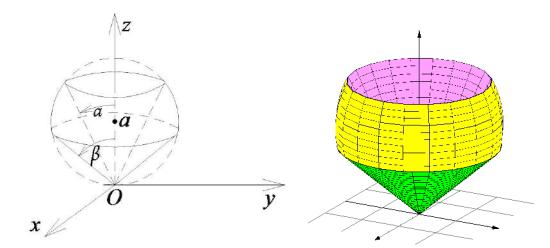
z2tg2β , если 0 α β π |
|
|
|
|
|
2 |
(рис. 53.4). |
|
|
|
|
Рис. 53.4
Пользуясь формулами, связывающими декартовы и сферические координаты, запишем уравнение исходной сферы с центром в точке (0,0,a)
и радиуса a в виде
ρ2 sin2 θcos2 ρ2 sin2 θsin2 ρ2 cos2 θ 2aρcosθ ,
что дает после преобразований ρ 2a cosθ .
Теперь можно задать область в сферических координатах условиями
0 ρ 2acosθ, 0 2π, α θ β .
Тогда объем находится следующим образом:
|
β |
2π |
2acosθ |
|
|
V ρ2 sinθ d dρdθ dθ |
d |
|
ρ2 sinθdρ |
||
|
α |
0 |
|
0 |
|
β 2π
dθ sinθ8a3 cos3 θd 4πa3 (cos4 α cos4 β) .
α 0 3 3
Заметим, что сферические и цилиндрические координаты являются ортогональными координатами (их координатные линии пересекаются под прямым углом). Иногда применяют и неортогональные координаты, но мы оставим это за рамками нашего рассмотрения.
53.2. Статические моменты, координаты центра тяжести, моменты инерции пространственных тел. Если пространственную область рассматривать как материальное тело, то с помощью тройного интеграла можно находить для него координаты центра тяжести и моменты инерции относительно некоторой плоскости, точки или оси. Формулу нахождения массы пространственного тела как интеграла от объёмной плотности мы уже получили.
Пусть ограниченное материальное тело в пространстве имеет объёмную плотность, заданную функцией γ γ(x, y, z) . Для определения
координат центра тяжести плоских областей использовались статические моменты относительно осей координат. Для пространственной области следует рассматривать статические моменты ,M xoy
относительно соответствующих координатных плоскостей.
Будем рассуждать так же, как при нахождении массы пространственного тела. Во-первых, разобьём тело на n тел. В пределах каждого тела i будем считать объёмную плотность постоянной и равной
её значению γ(xi , yi , zi ) в некоторой точке Pi (xi , yi , zi ) . Если далее считать,
что вся масса Mi подобласти i сосредоточена в точке Pi (xi , yi , zi ) , то можно рассматривать тело как систему материальных точек. Тогда для
статического момента относительно координатной плоскости |
yOz |
||
получим приближённое значение, |
выраженное через объём Vi |
части |
|
пространства, занимаемого телом i |
|
|
|
n |
n |
|
|
M yoz xi Mi |
xi |
γ(xi,yi,zi) Vi . |
|
i 1 |
i 1 |
|
|
При диаметре разбиения, стремящемся к нулю, интегральные суммы перейдут в пределе в двойной интеграл
M yoz xγ(x, y, z)dxdydz .
Аналогично получаются статические моменты относительно других координатных плоскостей. С помощью этих статических моментов вычисляются координаты центра тяжести тела по формулам
|
|
|
|
|
x |
|
M yoz |
, |
y |
M |
xoz , |
z |
|
|
Mxoy |
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
c |
|
|
M |
|
c |
|
M |
c |
|
|
M |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При постоянной объёмной плотности эти формулы приобретают вид |
|
||||||||||||||||||||||
x |
1 |
|
xdxdydz, |
y |
|
1 |
|
ydxdydz, |
z |
|
|
1 |
|
zdxdydz |
. |
||||||||
|
|
|
|
||||||||||||||||||||
c |
V |
|
c |
|
V |
|
|
|
|
c |
|
V |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
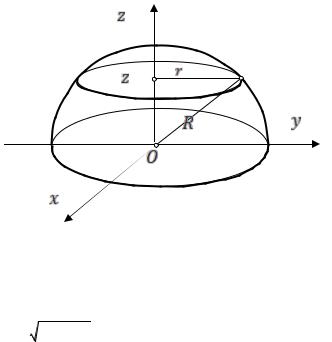
Найдем для примера центр тяжести однородного полушара радиуса R с |
||||||||||||||||||||||
центром в начале координат (рис. 53.5). |
|
Из соображений симметрии ясно, |
|||||||||||||||||||||
что две координаты центра тяжести |
xc и |
yc равны 0 . Чтобы вычислить zc |
|||||||||||||||||||||
, записываем соответствующую формулу |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
2πR3 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
z |
|
|
3 |
|
|
zdxdydz . |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 53.5
Учитывая, что сечение D полушара |
плоскостью z const представляет |
||||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
собой круг радиуса |
|
|
R2 z2 |
(рис. 53.5) с площадью |
S(z) π(R2 z2) , |
||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
R |
|
|
R |
2 |
|
2 |
|
πR4 |
|
||
zdxdydz |
zdz dxdy zS(z)dz zπ(R |
z |
)dz |
. |
|||||||||||||
|
|
4 |
|||||||||||||||
|
0 |
|
Dz |
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
Окончательно найдем |
zc |
3 |
|
πR4 |
|
3 |
R . |
|
|
|
|
|
|
||||
2πR3 |
4 |
8 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
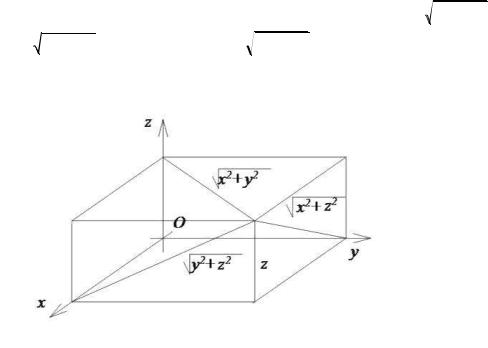
Моменты инерции относительно осей, точек и координатных плоскостей для пространственных тел определяются аналогично моментам инерции плоских фигур: интегрируется произведение плотности на квадрат расстояния до оси, точки или плоскости. Нужно учесть при этом, что
расстояние от произвольной точки P(x, y, z) до оси Ox равно 
 y2 z2 , до оси Oy равно
y2 z2 , до оси Oy равно 
 x2 z2 , до оси Oz равно
x2 z2 , до оси Oz равно 
 x2 y2 , до плоскости xOу равно z и так далее (рис. 53.6).
x2 y2 , до плоскости xOу равно z и так далее (рис. 53.6).
Рис. 53.6
Поэтому момент инерции относительно оси Ox записывается в виде
Ix (y2 z2)γ(x, y,z)dxdydz ,
момент инерции относительно координатной плоскости xOу
Ixoy z2γ(x, y,z)dxdydz ,
аналогично – для других осей координат и координатных плоскостей. Момент инерции относительно начала координат равен
I0 Ixoy Ixoz I yoz .
Записанные формулы упрощаются в случае однородных пространственных тел с постоянной объёмной плотностью.
Найдем для примера момент инерции тела, полученного в результате вращения вокруг оси Oz криволинейной трапеции aABb (рис. 53.7) относительно его оси симметрии.
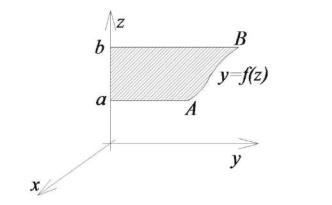
Рис. 53.7
Здесь y f (z) – неотрицательная и непрерывная на отрезке a,b |
функция. |
||
|
|
|
|
Считаем объёмную плотность |
постоянной γ(x, y, z) γ и |
используем |
|
выписанную ранее формулу в виде |
|
|
|
Iz γ (x2 y2 )dxdydz . |
|
|
|
|
|
|
|
Вычисляем тройной интеграл |
|
|
|
b |
|
|
|
Iz γ dz (x2 y2 )dxdy , |
|
|
|
a |
Dz |
|
|
где Dz – сечение исходного тела вращения плоскостью z const , которое представляет собой круг радиуса y(z) . Если D - круг радиуса R с центром в начале координат, то, переходя к полярным координатам, можно найти
|
2π |
|
R |
|
|
2π r4 |
|
Rd πR4 . |
||||
|
|
|
|
|
||||||||
(x2 y2 )dxdy d (r 2 cos2 r 2 sin2 )rdr |
|
|||||||||||
D |
0 |
|
0 |
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда для тела вращения вместо R достаточно подставить его выражение |
||||||||||||
как функцию y(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
y4 ( z) |
|
πγ |
b y 4 ( z)dz |
|
|
|
|
|
I z |
γ |
|
π |
dz |
|
|
|
|
||||
|
|
. |
|
|
|
|||||||
|
|
2 |
|
2 |
|
|
|
|
||||
|
|
a |
|
|
|
|
a |
|
|
|
|
|
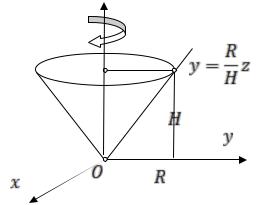
Полученную формулу удобно использовать для вычисления моментов инерции конкретных тел вращения. Например, для конуса радиуса R и высоты H с постоянной плотностью γ(x, y, z) γ (см. рис. 53.8) имеем
|
|
|
|
Рис. 53.8 |
|
|
||
|
πγ H R |
4 |
πγR4 |
3MR2 |
||||
I z |
|
|
|
z dz |
|
H |
|
, |
|
|
|
|
|||||
|
2 |
0 H |
|
10 |
|
10 |
|
|
так как его масса
M γ πR2 H .
3
Раздел 10. Криволинейные интегралы
Лекция 54. Криволинейный интеграл 1-го рода (по длине дуги)
54.1. Определение. К понятию криволинейного интеграла 1-ого рода приводит вычислительная конструкция, возникающая, например, при попытке точного решения задачи об определении массы неоднородной
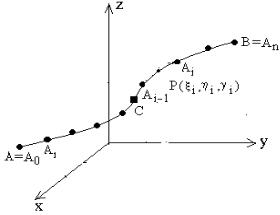
материальной линии. Задача формулируется так. Пусть в каждой точке P(x, y, z) линии AB в пространстве определена плотность ρ(x, y, z)
(рис. 54.1). Требуется найти массу этой линии.
Рис. 54.1
Под плотностью |
массы |
вдоль кривой AB |
в точке P0 (x0 , y0 , z0 ) |
||||
понимается величина |
ρ (x , y , z ) lim |
m , где |
l – длина отрезка |
||||
|
0 |
0 |
0 |
0 |
l 0 |
l |
|
|
|
|
|
||||
кривой, содержащего точку P0 (x0 , y0 , z0 ) , а m – масса этого отрезка. Если плотность в каждой точке линии одинакова и равна ρ0 , то масса вычисляется по формуле M ρ0 L , где L – длина кривой от точки A до точки B . Если же
плотность вдоль линии изменяется, то эта формула неприменима. Разовьем следующую идею приближенного вычисления массы этой
линии. Разделим |
линию |
AB на |
n |
небольших |
участков точками |
|
A0 A , A1, A2 , A3 ,..., An |
B и |
будем считать, |
что на участке Ai 1 Ai |
плотность |
||
постоянная, например, |
такая, как |
в |
некоторой |
точке |
P(ξi , ηi , νi ) , |
|
принадлежащей, отрезку кривой Ai 1 Ai . Тогда масса участка Mi |
|
может быть |
||||||
приближенно вычислена по формуле M |
i |
ρ(ξ |
, η , ν |
) l |
, |
где l |
i |
есть длина |
|
i |
i i |
i |
|
|
|
||
участка линии от точки Ai 1 до точки Ai . Масса всей линии может быть приближенно вычислена по формуле
n |
n |
M Mi |
ρ(ξi , ηi , νi ) li |
i 1 |
i 1 |
В силу интегральной методологии естественно ожидать, что точное значение массы может быть получено в результате предельного перехода
n
M lim (ξi , ηi , νi ) li (54.1)
n i 1
