
9623
.pdf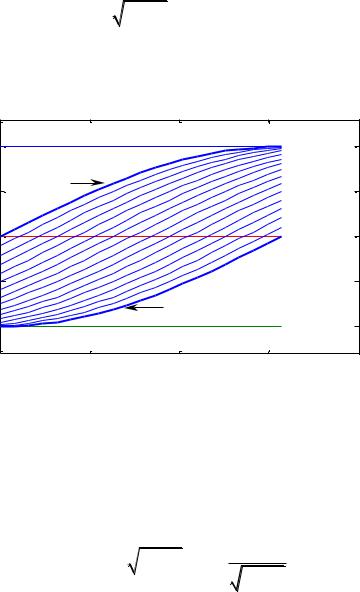
Теорема Коши. Пусть функция |
f (x, y) и ее частная производная |
|||||||||
fy (x, y) по переменной |
y непрерывны в области |
|
D . Тогда через любую |
|||||||
точку (x0 , y0 ) этой области проходит единственная интегральная кривая |
||||||||||
y y(x) , |
соответствующая |
решению, |
удовлетворяющему |
начальному |
||||||
условию y(x0 ) y0 . |
|
|
|
|
|
|
|
|
|
|
Точки, в которых нарушаются условия теоремы Коши, называют |
||||||||||
особыми. Через особые точки может проходить, вообще говоря, не одна |
||||||||||
интегральная кривая. Например, решениями уравнения |
|
|||||||||
|
|
|
|
y 1 y2 |
|
|
|
|
|
|
в области |
0 x ; |
1 y 1 служат функции |
y(x) sin(x C) и y 1 |
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
(см. рис. 40.2). |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0.5 |
y = sinx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = sin(x-pi/2) = - cosx |
|
||||
|
-1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0.5 |
|
1 |
|
1.5 |
2 |
|
|
|
|
|
|
Рис. 40.2 |
|
|
|
|
|
Из рисунка видно, |
что через точку |
(0; 1) |
|
проходят две кривые, |
||||||
являющиеся графиками функций |
y(x) sin(x ) cos(x), |
y 1. Это |
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
произошло потому, что в этой точке нарушено условие теоремы о |
||||||||||
непрерывности частной производной |
|
|
|
|
|
|||||
|
|
|
|
( |
1 y2 ) |
|
y |
. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
y |
1 y2 |
|
||
|
|
|
|
|
|
|
|
|||
40.2. Метод изоклин. Конечно, имея формулу, определяющую общее решение дифференциального уравнения, можно, вообще говоря, построить интегральные кривые. Возникает вопрос, нельзя ли по виду дифференциального уравнения выяснить некоторые свойства его интегральных кривых? Оказывается можно. Действительно, пусть

интегральная кривая y y(x) проходит через некоторую точку (x0 , y0 ) в
области определения функции в правой части (40.4). Проведем касательную к этой кривой в данной точке (рис. 40.3).
Рис. 40.3
Тогда тангенс угла наклона касательной будет равен
tg y (x0 ) f (x0 , y0 ) ,
где последнее равенство имеет место в силу того, что функция y y(x) –
решение уравнения (40.4). Таким образом, в каждой точке, где определена функция f (x, y) , нам известен угол наклона касательной к интегральной
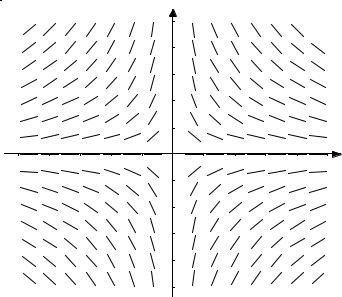
кривой, проходящей через эту точку. Если вообразить, что в каждой точке проведен такой отрезок касательной, то мы получим так называемое поле направлений данного дифференциального уравнения. Например, для уравнения (40.5) поле направлений приведено на рис. 40.4.
Поле направлений можно также получить, построив в каждой точке вектор d {1, f (x, y)}. Глядя на поле направлений, можно получить
некоторое представление о соответствующем семействе интегральных кривых (см. рис. 40.4). Векторы направления удобно строить единичной длины
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
, f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
f |
2 |
1 |
f |
2 |
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 40.4. |
|
|
|
|
|
|
Покажем, что если некоторая |
|
кривая |
y y(x) |
проходит через точку |
|||||||||
(x0 , y0 ) т.е. |
y0 y(x0 ) и касается направления поля в этой точке, то функция |
||||||||||||
y y(x) |
будет |
решением |
уравнения. |
Касание |
|
кривой |
заданного |
||||||
направления приводит к равенству векторов |
|
|
|
|
|||||||||
{1, y (x0 )} {1, f (x0 , y0 )}.
Из этого равенства сначала следует, что 1, а потом
y (x0 ) f (x0 , y0 ) f (x0 , y(x0 )) .
Если это свойство (касание кривой заданного направления) происходит в каждой точке некоторого промежутка, т.е.
y (x) f (x, y(x)), |
a x b, |
то последнее равенство и означает, что |
функция y y(x) решение |
уравнения в указанном промежутке.
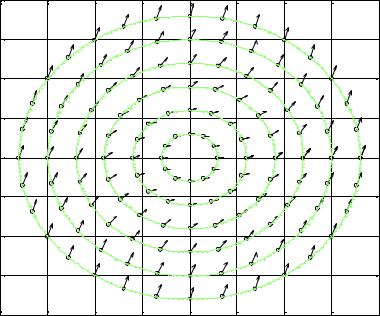
Эффективным способом построения поля направлений является так называемый метод изоклин. Изоклиной (кривой равного наклона) называется множество всех точек (x0 , y0 ) , в которых угол наклона
касательной один и тот же. Из (40.4) следует, что изоклина с данным коэффициентом k является кривой, которая задается уравнением
f (x, y) k .
Построив эти кривые при некоторых значениях |
k |
и, проводя на этих |
||||||
кривых отрезки касательных под соответствующим углом, получим поле |
||||||||
направлений. Например, для уравнения |
|
|
|
|
|
|||
|
|
|
y x2 y2 |
|
|
|
||
изоклинами служат окружности |
x2 y2 |
k (см. рис. 40.5). |
|
|||||
2 |
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
-1.5 |
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
-2 |
-1.5 |
-1 |
-0.5 |
0 |
0.5 |
1 |
1.5 |
2 |
Рис. 40.5.
Вообще говоря, нахождение решения дифференциального уравнения в виде формулы, связывающей независимую и зависимую переменные, представляет собой непростую задачу. Более того, для некоторых уравнений решение не может быть выражено через известные функции. Про такие уравнения говорят, что они не интегрируются в квадратурах. Странность термина объясняется тем, что вычисление интеграла исторически связано с вычислением площадей фигур – квадратурами. В этих случаях применяются разного рода численные методы, позволяющие на компьютере приближенно построить интегральные кривые. Однако, существуют классы дифференциальных уравнений, интегрируемых в квадратурах, т.е. для которых решение может быть найдено аналитически. Рассмотрим некоторые из них.
Лекция 41. Методы решений дифференциальных уравнений первого порядка
41.1. Уравнения с разделяющимися переменными. Если в
дифференциальном уравнении |
|
|
|
|
dy |
f (x, y) |
(41.1) |
|
dx |
||
|
|
|
|
правая часть может быть представлена в виде произведения функций f (x, y) f1 (x) f2 ( y) ,
то такое уравнение называют уравнением с разделяющимися переменными. Решают его следующим образом. Произведём разделение переменных, записывая уравнение
|
|
|
|
|
dy |
|
f (x) f |
|
( y) |
|
(41.2) |
|||||||
|
|
|
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
dx |
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
f (x)dx |
, |
|
(41.3) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
f2 ( y) |
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
предполагая, что f2 ( y) 0 . Поскольку |
|
y |
– некоторая функция |
x , то, |
||||||||||||||
учитывая инвариантность формы первого дифференциала, получим |
|
|||||||||||||||||
|
|
dy(x) |
|
|
|
dy |
f (x)dx . |
|
||||||||||
|
|
|
|
|
|
|
||||||||||||
f |
|
( y(x)) |
f |
|
( y) |
|
1 |
|
||||||||||
2 |
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Предположим, что последние два интеграла выражаются через элементарные функции в виде
F2 ( y) F1(x) C .
Таким образом, мы получили общее решение уравнения (41.3). Сюда следует добавить также решения вида y y , где f2 ( y ) 0 , которые мы
«потеряли» при делении уравнения (41.2) на функцию f2 ( y) .
41.2. Задача о форме вращающегося ножа. Начнем с примера.
Пусть режущая кромка ножа – прямая. Оказывается, если нож перемещается под прямым углом к своей режущей кромке, то разрезание происходит «хуже», чем в том случае, когда этот угол острый. Например, отрезая хлеб или другой продукт, мы, как правило, перемещаем нож под некоторым углом (см. рис. 41.1).
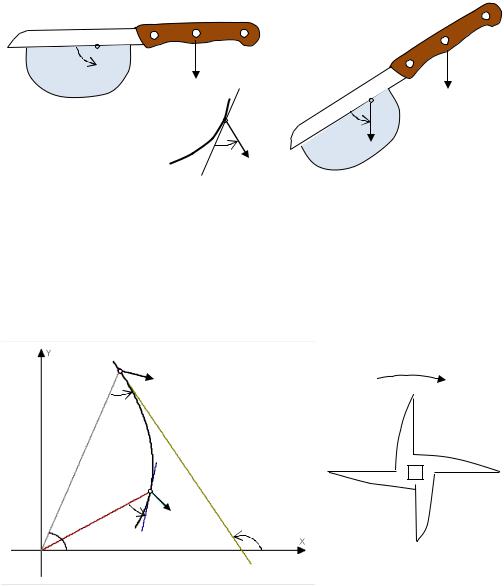
90° 
α
Рис. 41.1
Во многих инструментах режущая часть вращается, как например нож мясорубки. Если нож мясорубки имеет вид как на следующем рисунке, то он будет резать плохо, как отмечено выше.
( , )
α
|
φ |
α |
ψ |
|
|
|
|||
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 41.2 |
|
Возникает вопрос: нельзя ли для вращающегося ножа отказаться от режущей кромки в виде прямой линии, но чтобы угол резания в каждой точке режущей кромки ножа был один и тот же. Ответ на этот вопрос важен с технической точки зрения для эффективной эксплуатации разного рода режущих инструментов.
Если режущая кромка ножа отлична от прямой линии, то под углом резания в данной точке будем понимать угол между касательной в этой точке к режущей кромке и направлением перемещения точки режущей кромки ножа (см. рис. 41.1).
Итак, пусть нож, режущая кромка которого имеет форму некоторой кривой Г, вращается вокруг точки O . Поскольку угол резания в каждой точке один и тот же, то также будет постоянным и угол OMT между радиус-вектором точки M (x, y) и касательной MT к этой кривой в точке
M (x, y) (см. рис.2). В математической постановке задача формулируется

следующим образом: найти такую кривую |
|
y f (x) , |
чтобы в каждой её |
||||||||||||||||||||||||||||||||||
точке M (x, y) угол между касательной MT и радиус-вектором |
OM был |
||||||||||||||||||||||||||||||||||||
постоянен и равен |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для обозначенных на рисунке углов имеем |
|
|
|
, |
|
причём |
|||||||||||||||||||||||||||||||
|
|
tg |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, а |
x . Используя формулу тангенса суммы |
|
|
||||||||||||||||||||||||||||||||||
tg y |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
tg( ) |
|
tg tg |
|
, |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
1 tg tg |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
получаем дифференциальное уравнение первого порядка |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
x |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 k y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где обозначено k tg . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Для его решения выполним |
подстановку |
|
|
y |
t |
, т.е. от зависимой |
|||||||||||||||||||||||||||||||
|
|
x |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
переменной |
y перейдем к новой переменной t , являющейся функцией x . |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как y t x , то |
y |
t |
x dx и приходим к уравнению с разделяющимися |
||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
переменными |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
t x |
dt |
|
|
k t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
1 kt |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 kt |
dt k |
dx |
|
|
|
|
||||||||||||||
Разделяем переменные и интегрируем |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
||||||||||||||||||||||
|
|
1 t2 |
x |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
arctgt |
k |
ln(1 t2 ) k ln |
|
x |
|
k ln C . |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
x2 y2 |
|||
Возвращаясь к «старым» переменным, имеем |
|
arctg |
|
k ln |
|
|
|
. |
|||||||||||||||||||||||||||||
|
x |
|
C |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Полученную зависимость удобнее представить в полярной системе координат, что приводит к уравнению
r Ce k .
Это так называемая логарифмическая спираль. Она была известна многим математикам семнадцатого века, например, Декарту и Торричелли. Логарифмическая спираль часто встречается как в живой, так и неживой природе. Раковины улиток, а также рога некоторых животных закручены
по логарифмической спирали. В подсолнухе семечки расположены по дугам, близким к логарифмическим спиралям.
Например, полагая = 0,5 и |
k 1 |
при 0 |
, мы получим |
|
|
2 |
|
часть дуги логарифмической спирали |
r 0,5 e , по которой можно |
||
выточить режущие кромки ножа для мясорубки с углом резания 45
(см. рис. 41.3).
Рис. 41.3
41.3. Однородные дифференциальные уравнения. Рассмотренная нами задача позволяет выделить ещё один тип дифференциального уравнения первого порядка, интегрируемого в квадратурах. Для его характеристики привлечём понятие однородной функции. Такая функция выделяется следующим свойством:
f (t x,t y) f (x, y) , t,
т.е. при умножении её аргументов на одно и то же число значение функции не изменяется. Если в этом тождестве положить t 1/ x , то
|
y |
|
y |
|
|
f (x, y) f (1, |
|
) |
|
|
, |
|
|
||||
|
x |
x |
|
||
т.е. однородная функция может быть представлена как функция отношения своих аргументов.
Уравнение y f (x, y) , у которого правая часть однородная функция, называется однородным уравнением и сводится подстановкой
y |
t(x) , |
y t x , |
y t x |
dt |
|
x |
dx |
||||
|
|
|
к уравнению с разделяющимися переменными. Действительно,
t x |
dt |
(t) |
или |
xdt ( (t) t)dx |
|
dx |
|||||
|
|
|
|
Предполагая, что (t) t 0 и x 0 , разделяем переменные и интегрируем
dt
(t) t ln x C .
Обозначая интеграл слева через (t) , получаем общее решение исходного уравнения в виде
( |
y |
) ln |
|
x |
|
C . |
|
|
|
||||||
|
|||||||
|
x |
|
|
|
|
||
|
|
|
|
|
|||
К этому следует добавить решения, которые могут быть потеряны при |
|||||||
делении на функцию (t) t . Метод |
|
решения однородных уравнений |
|||||
открыл Иоганн Бернулли в 1695 году.

Лекция 42. Линейные дифференциальные уравнения. Приближенные методы решений дифференциальных уравнений первого порядка
42.1. Решение линейного уравнения и уравнения Бернулли.
Линейным дифференциальным уравнением первого порядка называется уравнение вида
A(x) y B(x) y C(x) 0
или, после деления на функцию A(x) , вида
y p(x) y q(x) 0 ,
в которые переменные y и y «входят» линейно. Покажем, что решение
этого уравнения может быть найдено в виде произведения двух функций, т.е.
y u(x)v(x) ,
каждая из них удовлетворяет уравнению с разделяющимися переменными. Подставляя y и производную y u v uv в исходное уравнение, его
можно представить в одном из следующих видов:
|
|
(42.1) |
u v u(v pv) q 0 |
||
или |
|
|
(u pu)v uv q 0 . |
|
|
Рассмотрим, например, первое уравнение. Выберем функцию |
v такую, |
|
чтобы выражение в скобке обратилось в ноль, т.е. удовлетворяющую дифференциальному уравнению с разделяющимися переменными относительно неизвестной функции v(x)
|
|
dv |
p(x)v 0 . |
|
|
|
|
|
|
dx |
|
Пусть v v (x) – одно из |
его решений (полученное, например, при |
||
постоянной интегрирования, |
равной нулю). При функции v v (x) |
||
уравнение (42.1) примет вид дифференциального уравнения с разделяющимися переменными относительно неизвестной функции u(x)
dudx v (x) q(x) .
Находя его общее решение в виде u u(x,C) , получим общее решение
