
9623
.pdf
|
|
e |
1 |
1 |
|
1 |
|
|
1 |
|
... |
1 |
|
|
|
e |
|
||
|
|
|
|
|
|
|
|
(n 1)! |
|||||||||||
|
|
|
|
1! |
|
2! |
3! |
|
n! |
|
|||||||||
где число |
находится на интервале (0,1). Очевидно, что на этом |
||||||||||||||||||
интервале |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
e 3 и потому |
|
|
|
. |
Так |
как |
|
|
8!= |
40320, то для |
|||||||||
(n 1)! |
(n 1)! |
|
|
||||||||||||||||
получения результата с заданной точностью достаточно вычислить первые 7 членов ряда (59.10) (их надо вычислять с точностью до 5-го знака, чтобы в результате суммирования не накопилась ошибка в 4 -ом знаке). Таким образом, чи сло e с точностью до 4-х знаков равно 2,7182.
Ряды Тейлора и Маклорена представляют собой разложения функций в степенные ряды. Они получены с помощью непосредственного вычисления значений производных в точке x=0. Можно получать такие разложения и другим и способами.
Найдем разложение функции f(x)=arctgx |
в степенной ряд |
|||||
методом интегрирования. Вспомним, что |
|
|||||
|
x |
1 |
|
|
||
arctgx |
|
|
dt. |
(59.12) |
||
|
|
|
||||
1 |
t 2 |
|||||
|
|
|
||||
|
0 |
|
|
|
|
|
Разложим подинтегральную функцию в ряд Маклорена. Для этого предварительно продифференцируем в области сходимости соотношение (59.5). Будем иметь
1 |
1 |
x x2 |
x3 ... ( 1)n xn ... |
|
|
||||
(1 x) |
||||
|
|
|
Подставим в это равенство вместо переменной x величину x2 . Получим требуемое разложение:
1 |
1 x2 x4 x6 ... ( 1)n x2n ... , |
|
1 x2 |
||
|
имеющее место при | x |<1. Подставив правую часть данного соотношения в равенство (59.12) и почленно проинтегрировав ряд, получим
arctgx x |
x3 |
|
x5 |
|
x7 |
... ( 1)n |
x2 n 1 |
... |
|
|
|
|
|
|
|||||
3 |
5 |
7 |
|
2n 1 |
|
||||
(59.13) |
|
|
|
|
|
|
|||
По ходу разложения мы находились в области | x |<1. Однако при x=1 и при x=-1 ряд в правой части равенства (59.13) по признаку
Лейбница также сходится. Поэтому равенство (59.13) имеет место в области -1≤x ≤1. Подставив x =1, получаем равенство
1 1 |
1 |
1 |
... ( 1)n |
1 |
|
... |
(59.14) |
||
2n 1 |
|||||||||
4 |
3 |
5 |
7 |
|
|
|
|||
59.3. Приложения степенных рядов. Приближенное вычисление функций. Как уже говорилось, степенные ряды позволяют с достаточной точностью вычислять значения функций с помощью простейших арифметических операций.
Пример. Вычислить с точностью до 0,001 значение функции
x |
sin t |
|
|
|
y |
|
dt |
при х=1. |
|
t |
||||
0 |
|
|
Будем считать, что подинтегральная функция при t=0 равна 1. Как известно, по формуле Ньютона – Лейбница данный интеграл вычислить не удается, ибо первообразная для подинтегральной
функции является |
|
неэлементарной |
функцией. Разложим |
|||||||||||||||
подинтегральную функцию |
в степенной ряд: |
|
|
|
|
|||||||||||||
|
sin t |
|
1 |
|
t3 |
t5 |
t 7 |
t 2 |
t 4 |
t 6 |
||||||||
|
|
|
|
|
|
(t |
|
|
|
|
|
....) 1 |
|
|
|
|
|
.... |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
t |
|
|
t |
|
3! |
5! |
7! |
3! |
5! |
7! |
|||||||
А теперь почленно проинтегрируем данный ряд в пределах от 0 до х, в результате чего получим разложение нашей функции y(x) в степенной ряд:
|
|
x |
sin t |
|
|
|
|
|
x3 |
|
|
x5 |
|
|
|
|
x7 |
|
|
||||||
|
y |
|
|
|
dt x |
|
|
|
|
|
|
|
|
|
|
.... |
|
||||||||
|
|
t |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
0 |
|
|
|
|
|
|
3 3! |
|
5 5! |
7 7! |
|
|
||||||||||||
Подставив в |
данный |
|
ряд |
|
|
х=1, |
|
получим |
сходящийся |
||||||||||||||||
знакочередующийся числовой ряд. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
1 |
1 |
|
|
|
|
1 |
1 |
|
1 |
…. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y(1) 1 3 3! |
5 5! 7 7! .... 1 18 600 |
5840 |
|||||||||||||||||||||||
|
|||||||||||||||||||||||||
Для получения |
значения |
|
|
y(1) с заданной точностью достаточно |
|||||||||||||||||||||
ограничиться первыми тремя слагаемыми, т. е. |
y(1)=0,946. |
|
|
||||||||||||||||||||||
59.4. Решение дифференциальных уравнений с помощью степенных рядов. С помощью степенных рядов возможно интегрировать дифференциальные уравнения. Рассмотрим линейное дифференциальное уравнение вида:
y(n) p1 (x) y(n 1) p2 (x) y(n 2) ... pn (x) y f (x) .
Будем искать решение этого уравнения, удовлетворяющее начальным условиям
y(x0 ) y0 , y (x0 ) y0 , …, y(n 1) (x0 ) y0 (n 1)
в некоторой малой окрестности точки x0. Представим искомое решение y(x) уравнения в виде степенного ряда с неопределенными коэффициентами
= 0 + 1 + 2 2 + .
Для нахождения неизвестных коэффициентов ci, данное выражение подставляется в уравнение, причем при необходимости все функции, входящие в уравнение также раскладываются в степенные ряды. Выполняя при этом необходимые действия со степенными рядами (дифференцирование, сложение, вычитание, умножение и пр.), приравниваются коэффициенты при одинаковых степенях в левой и правой частях данного уравнения. В результате с учетом начальных условий получается система уравнений, из которой последовательно определяются коэффициенты ci.
Отметим, что этот метод применим и к нелинейным дифференциальным уравнениям.
Пример. Найти решение уравнения y xy 0 c начальными условиями y(0) 1, y (0) 0 . Решение ищем в виде
= 0 + 1 + 2 2 + .
Отсюда
′ = 1 + 22 + 33 2 + 44 3 +
′′ = 22 + 63 + 124 2 + 205 3 +
Подставляем полученные выражения в исходное уравнение:
(2c2 6c3 x 12c4 x2 20c5 x3 ...) (c0 x c1x2 c2 x3 c3x4 ...) 0
2c2 x(6c3 c0 ) x2 (12c4 c1 ) x3 (20c5 c2 ) x4 (30c6 c3 ) ... 0
Приравнивая коэффициенты при всех степенях х к 0, получаем систему уравнений для определения коэффициентов:
2c2 0, |
6c3 c0 0 , 12c4 c1 0, 20c5 c2 0, 30c6 c3 0 |
||
… |
|
|
|
С учётом начальных условий |
c0 1, c1 0 , |
получаем, |
|
c 1; |
c 0; |
c |
|
0; |
c |
1 |
|
; |
c |
|
0; |
c 0; |
c |
1 |
; ... |
|||||
2 |
|
4 |
|
|||||||||||||||||
0 |
1 |
|
|
3 |
6 |
|
|
|
|
|
|
|
5 |
6 |
180 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
y 1 |
x3 |
|
x6 |
|
|
|
|
|
||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|||
|
|
6 |
|
180 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

Существует и другой метод решения дифференциальных уравнений с помощью рядов. Он носит название метод последовательного дифференцирования. Рассмотрим тот же пример. Решение дифференциального уравнения будем искать в виде разложения искомой функции в ряд Маклорена
y y(0) y (0) x y (0) x2 y (0) x3 ...
1! 2! 3!
Запишем дифференциальное уравнение в виде y xy . Если подставить заданные начальные условия y(0) 1, y (0) 0 . в уравнение, то получим, что y (0) 0. Теперь будем последовательно дифференцировать уравнение по х и находить значения всех производных в точке x=0:
y y xy ; |
y (0) y(0) 1; |
||
yIV y y xy ; |
yIV (0) 0; |
||
yV 2 y y xy ; |
|
yV (0) 0; |
|
yVI 3y y xyIV ; |
yVI (0) 4;... |
||
После подстановки полученных значений найдем
|
x3 |
|
x6 |
|||
y 1 |
|
|
|
|
... . |
|
6 |
180 |
|||||
|
|
|
||||
Лекция 60. Ряды Фурье
60.1. Введение. Рассмотрим тригонометрический ряд
a0 |
|
|
|
an cos nx bn sin nx A0 |
An sin(nx n ) , |
||
2 |
|||
n 1 |
n 1 |
представляющий собой сумму «гармоник» с целочисленными частотами. Нам удобнее далее иметь ряд в форме, указанной первой. Что ряды такого вида имеют право на существование, показывает следующий пример:
|
sin nx |
|
1 |
|
1 |
|
|
1 |
|
||
|
|
|
sin x |
|
sin 2x |
|
sin 3x |
|
|
sin 4x |
|
n |
2 |
4 |
9 |
16 |
|||||||
n 1 |
|
|
|
|
|
|
|||||
Действительно, для любого значения |
x |
мы имеем оценку |
|||||||||

|
|
|
sin nx |
|
1 |
, |
|
||
|
|
|
n2 |
|
n2 |
|
|||
|
|
|
|
1 |
|
|
2 |
|
|
причём |
известно, что |
|
|
|
|
|
1,65 . |
Следовательно, |
|
|
2 |
|
|||||||
|
|
|
n 1 |
n |
|
|
|
6 |
|
тригонометрический ряд сходится всюду и представляет собой некоторую функцию.
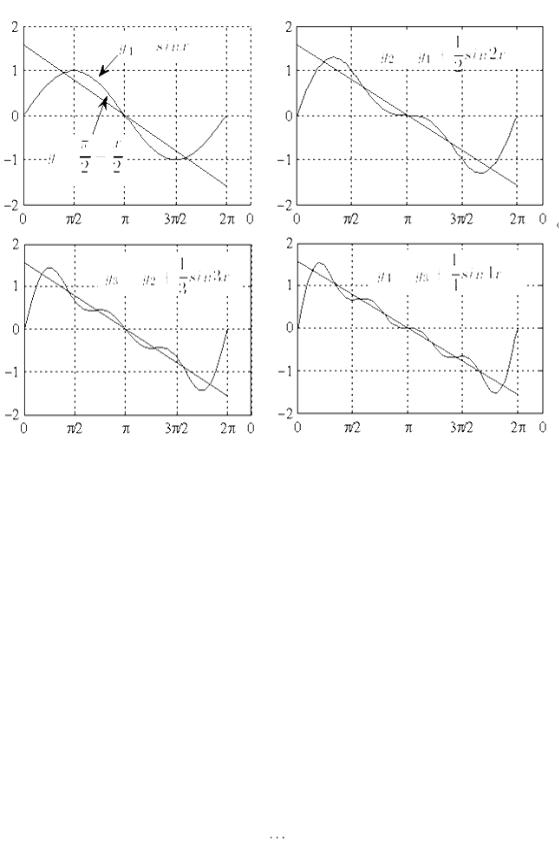
Немного истории. С периодическими движениями приходится иметь дело в самых различных областях знания – в физиологии (периодические колебания сердечной мышцы), музыке, акустике, электротехнике, теории упругости и т.д. И всюду простейшими периодическими движениями являются гармонические колебания. Что сложные колебания звука представляют собой сумму гармоник, человек понял, создав первый музыкальный инструмент. Исаак Ньютон показал, что такое интересное явление природы, как радуга, это разложение белого цвета на его составляющие. Случаи разложения некоторой функции на гармоники тоже были известны. Так, в 1744г. Л. Эйлер опубликовал пример:
|
|
x |
sin x |
1 sin 2x |
1 sin 3x |
, |
0 x 2 |
|
(60.1) |
|
2 |
2 |
|
2 |
3 |
|
|
|
|
На рис. 60.1 приведены графики функции левой части этого выражения |
|||||||||
и первых пяти слагаемых правой части. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Рис. 60.1 |
|
|
|
|
|
Впервые тригонометрические ряды как метод решения возник при |
|||||||||
изучении уравнения, описывающего колебания струны. В 1753г. Даниил |
|||||||||
Бернулли (1700-1782) пришел к выводу, что самыми общими решениями уравнения струны должны быть решения в виде линейных комбинаций стоячих волн, т.е. в виде тригонометрического ряда. Как ни странно, Эйлер
сэтим не согласился. Он сомневался в возможности представления произвольной функции тригонометрическим рядом. В 1759г. Ж.Л.Лагранж (1736-1813), изучая колебания уже не струны, а аппроксимирующей её нити
снанизанными «бусинками», и затем совершая предельный переход, «почти примирил» противоречивые точки зрения Бернулли и Эйлера.
В 1807г. Ж.Фурье (1768-1830) вывел уравнение, описывающее распространение тепла в твёрдом теле и применил тригонометрические ряды к его решению. Анализ Фурье не был принят сразу. Когда Фурье огласил его на одном из заседаний французской академии наук, Лагранж заявил, что это невозможно. Тем не менее, академия удостоила Фурье премии за математическую теорию теплопроводности (с оговорками относительно строгости и общности применяемого им метода). Публикация была отложена до 1815г. Идеи Фурье положили начало глубокому изучению теории тригонометрических рядов, где на многие возникшие там вопросы до сих пор нет ответов. Так в 1829г. немецкий математик Дирихле (1805-1859) нашёл условия, при которых функция может быть представлена тригонометрическим рядом. В 1853г. немецкий математик Риман (18261866), изучая условия, при которых функция представляется тригонометрическим рядом, пришёл, в частности, к своему известному определению интеграла (которым мы и пользуемся).
Рассмотрим теперь на графике, как «приближаются» частичные суммы ряда в примере Эйлера к функции, являющейся его суммой.
Рис. 60. 2
Мы видим, что чем больше гармоник, тем график их суммы «ближе» к графику функции
y ( x) / 2 .
Не будем детально вникать в смысл понятия «сходимости» последовательности частичных сумм ряда к его сумме. Просто будем помнить, что при каждом фиксированном x тригонометрический ряд сходится к значению f (x) как числовой ряд.
60.2. Коэффициенты ряда Фурье. Если функция y f (x)
«допускает» представление в виде тригонометрического ряда
|
a0 |
|
|
|
f (x) |
an cos nx bn sin nx , |
(60.2) |
||
|
||||
2 |
n 1 |
|
||
то задача получения такого разложения в ряд сводится к нахождению
коэффициентов a0 , an ,bn , n 1, 2, |
. Проделаем формально следующую |
|
операцию: проинтегрируем равенство (60.2) от |
до : |
|
|
|
a0 |
|
|
|
|
|
|
f (x)dx |
dx an cos nxdx bn cos nxdx. |
|||||
2 |
|||||||
|
|
|
|
n 1 |
|
|
|
Поскольку все интегралы под знаком суммы равны нулю, то мы получаем
1
a0 f (x)dx .
Ясно, что для существования интеграла подынтегральная функция должна быть «достаточно хороша». С другой стороны, многое в теории рядов Фурье становится более естественным и понятным, если расширить само понятие интеграла до так называемого интеграла Лебега. Мы ограничимся понятием интеграла Римана, которым до сих пор пользовались.
Функцию f (x) будем предполагать далее
интеграл
f (x) dx .
В частности, это не исключает наличия разрывов функции.
Вернёмся теперь к правой части равенства (60.2), которую мы почленно проинтегрировали, что не всегда законно. Для этого ряд должен обладать определёнными свойствами, которые мы также не будем здесь обсуждать. Продолжаем «добывать» остальные коэффициенты. Умножим
обе части равенства на функцию cos nx |
при любом, но фиксированном |
|
значении n 1, 2, . |
Затем опять проинтегрируем по промежутку , . |
|
Справа получаем |
|
|
|
|
|
am cos mx cos nxdx bm sin mx cos nxdx . |
||
m 1 |
|
|
Первый член исчез, а «немой» индекс суммирования мы сменили. Под знаком суммы также «пропадут» все слагаемые кроме одного, а именно члена ряда с номером m n . В самом деле, если m n, то
|
1 |
|
|
||
sin mx cos nxdx |
|
sin(m n)x sin(n m)x dx 0, |
|||
2 |
|||||
|
|
|
|
||
|
1 |
|
|
||
cos mx cos nxdx |
|
|
cos(m n)x cos(n m)x dx 0 |
||
|
2 |
||||
|
|
|
|
||

|
|
|
|
|
1 |
|
|
|
|
В случае, когда m n , имеем |
|
cos2 nxdx |
|
1 cos 2nx dx , |
|||||
|
2 |
||||||||
|
|
|
|
|
|
|
|
||
поэтому |
|
|
|
|
|
|
|
|
|
a |
|
1 |
|
|
f (x) cos nxdx . |
(60.3) |
|||
|
|
|
|||||||
|
|
|
|||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При n 0 мы получаем формулу для вычисления |
a0 , что и объясняет, |
||||||||
почему начальный член ряда обозначен нами через a0 |
2 . |
||||||||
Аналогичным образом, умножая равенство |
(60.2) на функцию sin nx |
||||||||
и интегрируя, получим формулу для вычисления коэффициента bn |
|||||||||
b |
|
1 |
|
|
f (x)sin nxdx . |
|
(60.4) |
||
|
|
|
|
||||||
|
|
|
|
||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Формулы (60.3) и (60.4) для коэффициентов |
an и bn называются |
||||||||
формулами Эйлера-Фурье, а сам ряд с такими коэффициентами называют рядом Фурье для функции f (x) , независимо от того, сходится ли
полученный ряд хотя бы в одной точке, а если где-то и сходится, то может оказаться, что совсем не к той функции, которая его «породила». Поэтому, пока не указаны условия сходимости ряда Фурье к той функции, из которой он получен, знака равенства в формуле (60.2) не ставят:
f (x) ~ a0 an cos nx bn sin nx .
2 n 1
Чтобы исключить «неприятности» такого рода, используем условия Дирихле, при которых ряд Фурье сходится к функции, его породившей.
Теорема. Если функция f (x) периода |
2 |
кусочно-монотонна в |
|||
промежутке , |
и имеет в нём не более, |
чем конечное число точек |
|||
разрыва, то её ряд Фурье сходится к сумме |
f (x0 ) в каждой точке |
||||
непрерывности и к сумме |
|
|
|
||
|
|
f (x0 0) f (x0 0) |
|
|
|
|
2 |
|
|
|
|
в каждой точке разрыва. |
|
|
|
||
Напомним, что |
символы f (x0 0) |
и |
f (x0 0) означают, |
||
соответственно, левый и правый пределы функции в точке x0 .
Пример 1. Составим ряд Фурье для функции
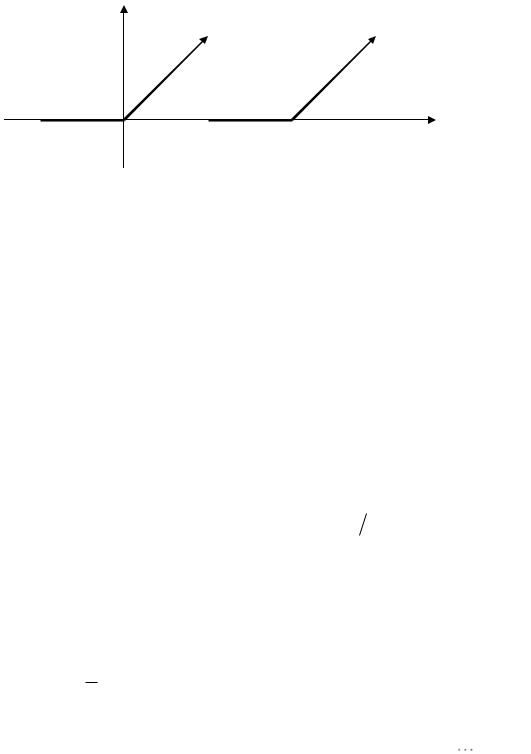
0, x 0 f (x)
x, 0 x
Поскольку ряд Фурье даст периодическую функцию (если он сходится), то продолжим далее эту функцию периодически с периодом 2π.
у
π –
׀ |
|
|
• |
• |
׀ |
|
-π |
0 |
π |
|
2π |
3π |
х |
Рис. 60.3
Получилась разрывная функция, определенная на всей числовой прямой, а значение функции в точке разрыва функции равно нулю. Вычисляем коэффициенты ряда Фурье:
a |
1 |
|
f (x) dx |
1 |
|
x dx |
1 |
|
x2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
0 |
|
|
|
2 |
|
|
|
2 |
||
|
|
|
|
|
0 |
|
|||||||
|
|
1 |
x cos n x dx |
1 |
|
1 |
|
an |
|
|
|
x |
|
||
|
|
n |
|||||
|
|
|
|
||||
|
|
0 |
|
|
|
|
|
|
|
|
n |
|
|
sin nx |
|
|
1 |
sin nx dx . |
|
|
|||||
|
0 |
|
|
0 |
|
Здесь была применена формула интегрирования «по частям». Далее
|
|
1 |
|
1 |
|
|
|
1 |
|
|
0, |
|
n четное |
|
|
|
|
|
|
|
|
|
|||||||
an |
|
|
|
|
|
cos nx |
|
|
|
|
cos n 1 |
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|||||||
|
|
|
|
n |
|
|
0 |
|
n |
|
2 |
n |
|
, n нечетное |
Таким образом, коэффициенты с четными номерами при косинусах в разложении отсутствуют.
Вычисляем коэффициенты при синусах:
1 bn 0
xsin nx dx |
1 |
|
|
x |
|
|
|
|
|||
|
|
||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
cos nx |
|
|
n 0 |
cos nx dx |
|
|
|
0 |
|
|
|
||
|
1 |
|
|
|
1 |
|
|
|
1 |
n 1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
cos n |
sin n |
|
|
|
, n 1, 2, |
||||
|
n |
n2 |
n |
||||||||
|
|
|
|
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Итак, ряд Фурье данной функции имеет вид:
