
9428
.pdf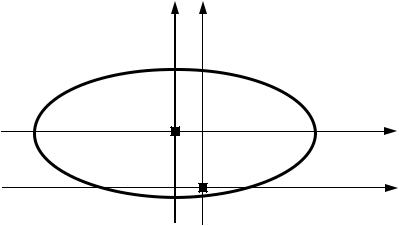
Пример. Привести к каноническому виду уравнение: x2 + 2x + 4 y2 - 16 y = 8 .
|
Решение. Здесь потребуется сначала выделить полные |
|||||
квадраты |
|
|
|
|
||
|
(x2 + 2x + 1)- 1+ 4(y2 - 4y + 4)- 16 = 8 |
|||||
или |
(x + 1)2 + 4(y - 2)2 = 25. |
|||||
Тогда после параллельного переноса, задаваемого формулами |
||||||
|
м |
|
|
|
|
|
|
пп xў= x + 1 |
, |
|
|||
|
н |
|
|
|
||
|
ппyў= y - 2 |
|
|
|||
|
о |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
уравнение приобретает вид |
xў |
+ |
yў |
= 1. |
||
25 |
25 |
|||||
|
|
|
|
|||
|
|
|
|
4 |
|
|
Получилось каноническое уравнение эллипса с полуосями a = 5
и |
b = 5 , центр которого находится в новом начале координат |
|||||
|
2 |
|
|
|
|
|
Oў(- 1;2). Отражаем это рисунком 6.3. |
||||||
|
|
2 |
|
2 |
|
|
|
Ответ: |
xў |
+ |
yў |
= 1. |
|
|
25 |
25 |
|
|||
|
|
|
|
|
||
|
|
|
|
4 |
|
|
|
|
|
|
|
y |
y |
O 2
x
1 O
x
Рис. 6.3
60

Классификация кривых второго порядка
Если исходное уравнение кривой второго порядка вида (5.1) содержит произведение координат x и y (т.е. B 0 ), то для приведения его к каноническому виду используется поворот системы координат (мы его здесь не рассматриваем).
Если же в уравнении (5.1) присутствуют переменные x и y
без квадратов ( D 0 или Е 0 ), то выполняется параллельный перенос осей координат для того, чтобы уравнение в новой системе координат приобрело канонический вид. Этих преобразований достаточно для решения поставленных задач.
Проанализируем возникающие ситуации. Для этого рассмотрим коэффициенты A и C при квадратах переменных в канонических уравнениях основных линий и найдём их произведение.
Для канонического уравнения эллипса A a12 , C b12 , т.е.
произведение AC 0 ;
для гиперболы A a12 , C b12 , т.е. AC 0; для параболы A 0 , C 1, т.е. AC 0 .
Остальные виды канонических уравнений можно распределить по типам таким образом, чтобы для каждого из уравнений первого типа число AC было положительно, отрицательно для второго и равно нулю для уравнений третьего типа. Тогда получаем классификацию:
61
I. Эллиптический тип:
|
x2 |
|
y2 |
|
|||
1) |
|
|
+ |
|
|
= 1 |
(эллипс или окружность), |
a |
2 |
b |
2 |
||||
|
|
|
|
|
|
||
|
x2 |
+ |
y2 |
= 0 |
|
|
2) |
|
|
(точка), |
|||
a2 |
b2 |
|||||
|
|
|
|
|
x2 |
+ |
y2 |
= - 1 (пустое множество). |
||||||||||||
3) |
|
|
|
|
|
|
|
|
|
|||||||
a |
2 |
b |
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
II. Гиперболический тип: |
||||||||||||||||
4) |
|
x2 |
- |
|
|
y2 |
|
= 1 |
(гипербола), |
|||||||
|
a2 |
|
b2 |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
x2 |
|
- |
|
|
y2 |
|
= 0 |
|
||||||
5) |
|
|
|
|
|
|
|
|
|
|
(пара пересекающихся прямых). |
|||||
|
a |
2 |
|
|
b |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
III. Параболический тип: |
||||||||||||||||
6) |
|
y2 = 2 px (парабола), |
||||||||||||||
7)y2 = a2 (пара параллельных прямых),
8)y2 = 0 (прямая),
9)y2 = - a2 (пустое множество).
Полученную классификацию можно использовать в любой задаче, связанной с уравнением второго порядка – даже если, например, в нём B 0 . Оказывается, по исходным коэффициентам уравнения (5.1), которые присутствуют в конкретной задаче, можно сразу определить, к какому типу относится линия, задаваемая этим уравнением:
I. Если |
AC B2 0 , |
то |
уравнение |
задаёт |
линию, |
относящуюся к эллиптическому типу. |
|
|
|||
II. Если |
AC B2 0 , |
то |
уравнение |
задаёт |
линию, |
относящуюся к гиперболическому типу. |
|
|
|||
|
|
62 |
|
|
|
III. Если |
AC B2 0 , |
то |
уравнение задаёт линию, |
относящуюся к параболическому типу. |
|||
Пример. |
Определить |
тип |
кривой, заданной уравнением |
xy 3.
Решение. В заданном уравнении A C 0, 2B 1. Так как
AC B2 14 0 , оно задаёт линию гиперболического типа, В
этом случае для построения можно пользоваться привычной записью уравнения гиперболы в виде y 3x (x 0) .
Ответ: уравнение задает кривую гиперболического типа. Итак, чтобы разобраться с построением линий по
уравнению второго порядка (5.1), нужно сначала определить тип линии, задаваемой уравнением. Далее приводят уравнение к каноническому виду, выполняя соответствующие преобразования координат.
§7. Поверхности второго порядка
Переходим к изучению поверхностей в трехмерном пространстве. Будем рассматривать поверхности, задаваемые уравнениями, включающими вторые степени текущих координат x , y и z или их взаимное произведение. Уравнение вида
Ax2 By2 Cz2 2Dxy 2Exz |
|
||||
2Fyz 2Gx 2Hy 2Kz L 0 , |
(7.1) |
||||
где коэффициенты A, B,C, D, E , F ,G , H , K и L |
— любые |
||||
действительные |
числа, |
но, по крайней |
мере, одно из чисел |
||
A, B,C, D, E |
или |
F |
отлично от |
нуля (т.е. |
|
A2 B2 C2 D2 E2 |
F 2 |
0), |
называется |
общим |
|
уравнением поверхности второго порядка. |
|
||||
|
|
|
63 |
|
|
Также как и для кривых второго порядка, для поверхностей второго порядка существует полная классификация. С помощью подходящего параллельного переноса и поворота осей координат (теперь уже выполняемых в пространстве) любое уравнение второго порядка может быть приведено к одному из семнадцати видов. Этим уравнениям в пространстве отвечают классические поверхности: эллипсоид, однополостный и двуполостный гиперболоиды, конус, эллиптический и гиперболический параболоиды, а также целая группа поверхностей, называемых цилиндрическими.
Цилиндрические поверхности
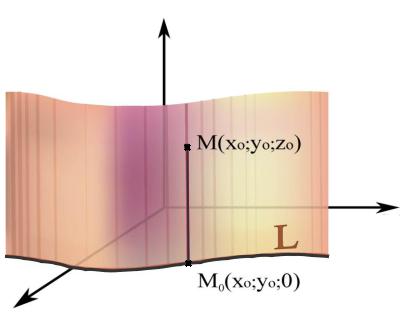
Поверхность, состоящая из параллельных прямых (так называемых образующих), проходящих через каждую точку заданной линии L (направляющей), называется
цилиндрической поверхностью. Образно можно представить,
что цилиндрические поверхности образуются движением прямой, которая перемещается в пространстве вдоль кривой L , сохраняя постоянное направление (рис. 7.1).
В качестве направляющей цилиндрической поверхности
рассмотрим расположенную в плоскости xOy линию L , |
которая |
|
задаётся уравнением |
F(x, y) 0 . Пусть M0 (x0 , y0 ,0) – |
|
произвольная точка |
направляющей (рис. 7.1). |
Тогда |
F (x0 , y0 ) 0 .
Рассмотрим цилиндрическую поверхность, образующие которой параллельны координатной оси Oz . Если такая
образующая проходит через M0 (x0 , y0 ,0) , то абсциссы всех её точек равны x0 , а ординаты равны y0 . Поэтому координаты произвольной точки M (x0 , y0 , z0 ) этой образующей тоже удовлетворяют уравнению F(x, y) 0 при любом значении z0 .
64
z
y
x
Рис. 7.1
Точка M0 (x0 , y0 ,0) выбиралась произвольно, поэтому можно утверждать, что координаты всех точек цилиндрической поверхности удовлетворяют уравнению F (x, y) 0 .
Ясно, |
что |
уравнение |
вида |
F (x, z) 0 |
задаёт |
цилиндрическую поверхность с |
образующими, параллельными |
||||
оси Oy , |
а уравнение вида F ( y, z) 0 |
задаёт цилиндрическую |
|||
поверхность с образующими, параллельными оси O x .
Если направляющей цилиндрической поверхности является кривая второго порядка, то поверхность называется цилиндрической поверхностью второго порядка (или цилиндром второго порядка). В зависимости от конкретного вида уравнения получаются различные типы цилиндров второго порядка. Их названия соответствуют названиям направляющих линий L .
Например, уравнение |
x2 |
|
y2 |
1 |
задаёт в пространстве |
|
a2 |
b2 |
|||||
|
|
|
|
цилиндрическую поверхность с образующими, параллельными оси Oz . Его направляющей является эллипс, а поверхность, задаваемая этим уравнением, называется эллиптическим
65
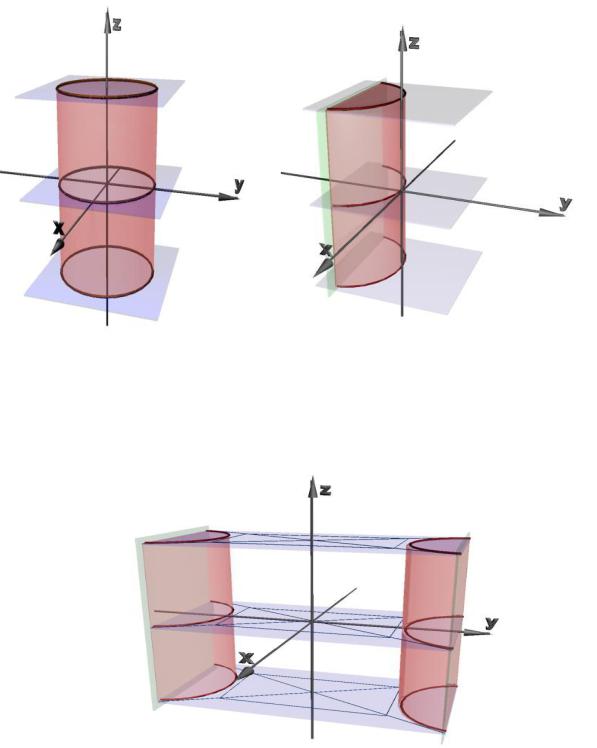
цилиндром (рис. 7.2). Частным случаем эллиптического цилиндра является круговой цилиндр. Его уравнение в
каноническом виде имеет вид x2 + y2 = R2 .
Уравнение вида x2 2 py определяет в пространстве
параболический цилиндр (рис. 7.2).
Рис. 7.2
Уравнение вида |
y2 |
|
x2 |
1 |
определяет в пространстве |
|
b2 |
a2 |
|||||
|
|
|
|
гиперболический цилиндр (рис. 7.3).
Рис. 7.3
66
Поверхности вращения Поверхности вращения образуются вращением какой-либо
плоской линии L (образующей) вокруг прямой (оси поверхности вращения), расположенной в плоскости этой линии. Примером служит сфера: её можно рассмотреть как поверхность, образованную вращением полуокружности вокруг её диаметра. Покажем, как можно получить уравнение поверхности вращения, исходя из уравнения образующей (лежащей в одной из координатных плоскостей) и уравнения оси вращения (совпадающей с одной из координатных осей, расположенных в той же плоскости).
Будем вращать расположенный в плоскости yOz эллипс с
уравнением |
y2 |
|
z2 |
1 |
вокруг |
координатной оси Oz . |
|
b2 |
c2 |
||||||
|
|
|
|
|
|||
Полученную поверхность |
рассечём |
плоскостью, параллельной |
|||||
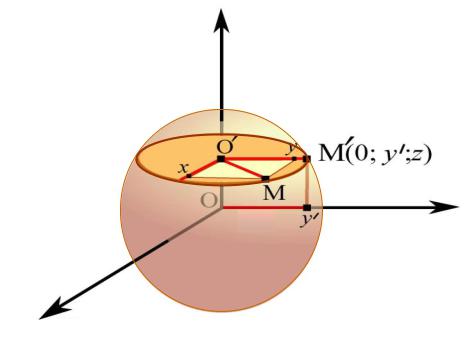
координатной плоскости xOy и проходящей через фиксированную точку O (0, 0, z) (рис. 7.4).
z
y
x
Рис. 7.4
67
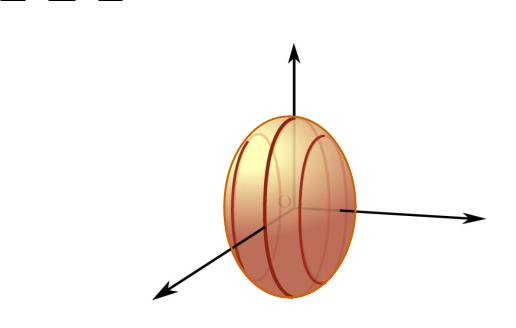
Пусть M (x, y, z) |
– произвольная точка поверхности вращения, |
||||
лежащая в плоскости сечения. Рассмотрим в |
плоскости yOz |
||||
точку поверхности |
M (0, y , z) . Её |
ордината |
по абсолютной |
||
величине равна |
радиусу окружности, на которой лежит точка |
||||
M (x, y, z) |
, т.е. O M O M , поэтому |
x2 y2 y 2 |
. Находящаяся в |
||
|
|
||||
плоскости yOz |
точка M (0, y , z) |
принадлежит и плоскости |
|||
сечения, и исходному эллипсу. Это означает, что её координаты
удовлетворяют уравнению |
y 2 |
|
z2 |
1. |
Подставляя в это |
||
b2 |
c2 |
||||||
|
|
|
|
|
|||
уравнение выражение y |
через |
x |
и y , |
получим |
|||
|
x2 |
|
y2 |
|
z2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1. Это |
и |
есть |
искомое |
уравнение |
поверхности |
|||
|
b |
2 |
b |
2 |
c |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
вращения, называемой эллипсоидом вращения. |
|
||||||||||||||||
|
|
|
Если вращать эллипс |
|
y2 |
|
z2 |
1 вокруг оси Oy , получится |
|||||||||
|
|
|
|
b2 |
c2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
другой |
|
эллипсоид |
вращения (рис. |
7.5) с |
уравнением |
||||||||||||
x2 y2 z2 1. c2 b2 c2
z
y
x
Рис. 7.5
68
От этих примеров нетрудно перейти к алгоритму получения уравнения поверхности вращения по уравнению исходной кривой, если осью вращения служит одна из координатных осей. В уравнении кривой слагаемое с переменной, наименование которой совпадает с наименованием оси вращения, останется без изменения, а квадрат другой переменной меняется на сумму квадратов этой переменной и переменной, отсутствовавшей в уравнении.
§8. Канонические уравнения поверхностей второго порядка
Теперь перейдем к другим поверхностям второго порядка, определяемым общим уравнением
Ax2 By2 Cz2 2Dxy 2Exz
2Fyz 2Gx 2Hy 2Kz L 0 .
Каждая поверхность может быть построена по её уравнению методом сечений. Проследим, как образуются поверхности второго порядка, проявляясь постепенно по мере стыковки разных сечений.
Эллипсоиды
Начнём с уравнения эллипсоида
x2 |
|
y2 |
|
z2 |
1 . |
|
|
|
|
|
(8.1) |
||||
a2 |
b2 |
c2 |
|||||
|
|
|
|
Уравнение сечения этой поверхности координатной плоскостью xOz получается, если в исходном уравнении (8.1) принять y 0 :
x2 |
|
z2 |
1 |
. По виду уравнения мы узнаём эллипс и можем |
|
a2 |
c2 |
||||
|
|
|
изобразить его в соответствующей плоскости (рис. 8.1).
69
