
9405
.pdf
Находя его общее решение в виде u = u(x,C) , получим общее решение исходного линейного дифференциального уравнения в виде
y = u(x,C)v (x) .
В качестве примера вернемся к уравнению m dy = mg − ky , которое
|
|
|
|
|
dt |
|
|
|
|
описывает изменение скорости y(t) падающего |
тела. |
Приведем это |
|||||||
уравнение к виду |
|
y ′ + a y = g , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где для краткости |
a = k / m . |
Подстановка |
y = uv |
приводит сначала к |
|||||
уравнению v ′ + a v |
= 0 , решение которого |
v (t) = e−at . |
Далее |
||||||
|
|
|
|
|
|
|
|
|
|
получим уравнение |
u ′ = ge a t |
, откуда найдем |
u |
= |
g |
e a t |
+ C . |
||
|
|||||||||
|
|
|
|
|
|
|
a |
|
|
Наконец, получим общее решение исходного уравнения |
|
|
|
|
|||||
|
y ( t ) = ( g a + C e − a t ) . |
|
|
|
|
|
|||
Отметим, что так называемое уравнение Бернулли, имеющее вид |
|||||||||
|
′ |
|
α |
= 0, |
|
|
|
|
|
|
y + p(x) y + q(x) y |
|
|
|
|
|
|
||
сводится к линейному уравнению следующим образом. Будем считать, что a ¹ 0 и a ¹1, т.к. оба эти случая соответствуют линейным уравнениям.
Поделим обе части уравнения на yα
y′ + 1−α + = yα p(x) y q(x) 0
и введем новую переменную z = y1−α . В новых переменных исходное уравнение будет линейным
1z′ + p(x)z + q(x) = 0 .
1− α
42.2.Приближенные методы решения дифференциальных уравнений первого порядка. Теперь остановимся на приближенных методах. Сначала рассмотрим метод Пикара (метод последовательных приближений). Представим задачу Коши
y′ = f (x, y), y(x0 ) = y0
21
в следующем эквивалентном виде: найти функцию y(x) такую, что
x
y(x) = y0 + ∫ f (x, y(x))dx .
x0
Фактически, мы заменили дифференциальное уравнение интегральным уравнением, в котором неизвестная функция y(x) входит ещё и под знак
интеграла. Если под знаком интеграла функцию y(x) заменить её значением y0 , получим так называемое первое приближение
x
y1(x) = y0 + ∫ f (x, y0 )dx .
x0
Затем заменяем y(x) найденной функцией y1 (x) и получаем второе приближение
x
y2 (x) = y0 + ∫ f (x, y1 (x))dx .
x0
Продолжая процесс далее, найдем
x
yn (x) = y0 + ∫ f (x, yn−1 (x))dx .
x0
Таким образом, получаем последовательность функций
y1 (x), y2 (x), K, yn (x), K |
(42.2) |
Оказывается, что при определенных условиях эта последовательность сходится к решению исходной задачи Коши. Под этим понимается, что для каждого x из рассматриваемого интервала числовая последовательность (42.2) имеет пределом соответствующее значение решения y(x) .
Справедлива следующая теорема, которую приведём без доказательства.
Теорема. Пусть в окрестности точки (x0 , y0 ) |
функция |
f (x, y) и ее |
|||
частная производная |
f y′(x, y) непрерывны. Тогда в некотором интервале, |
||||
содержащем точку |
x0 , последовательность |
функций (42.2) сходится к |
|||
функции |
y(x) , являющейся решением |
задачи |
Коши |
для данного |
|
уравнения.
Пример. Решим этим методом следующую задачу
y′ = x − y, y(0) = 1, y(x) = ?
|
x |
Запишем уравнение в интегральной форме |
y(x) = 1 + ∫(x − y)dx . |
|
0 |
Подставив под знаком интеграла вместо неизвестной функции y(x) начальное значение y0 = 1 , получим первое приближение
22
|
|
|
|
x |
|
|
2 |
|
|
|
|
|
|
|
|
y1 (x) = 1 + ∫(x − 1)dx = 1 − x + x |
. |
|
|
|
|
|
|||
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Второе приближение получаем, вычисляя интеграл |
|
|
|
|
|
|
||||||
|
|
|
x |
|
|
|
|
|
3 |
|
|
|
|
|
y2 (x) = 1 + ∫(x − y1 (x))dx = 1 − x + x2 − x |
. |
|
|
|
||||||
|
|
|
0 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
0.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2=1-x+x2-x3/6 |
|
|
|
|||
0.8 |
|
|
|
|
|
|
|
|
|
|
|
|
0.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=2exp(-x)+x-1 |
|
|
|
||
0.6 |
|
y1=1-x+0.5x2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
0.5 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
|
0.7 |
|
0.8 |
|
|
|
0 |
|
|
|
||||||||
|
|
|
|
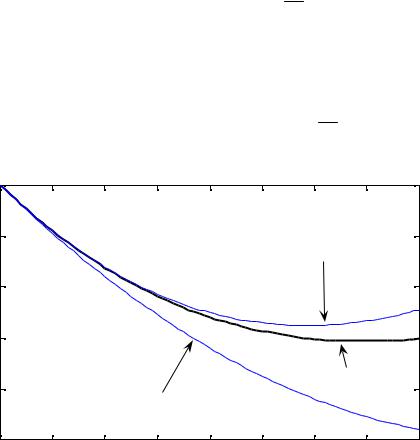
Рис. 42.1 |
|
|
|
|
|
|
|
|
На рис. 42.1 |
приведены графики точного решения |
y(x) = 2e− x |
+ x −1 и |
|||||||||
два полученных приближения. Существуют оценки погрешности метода |
||||||||||||
Пикара, которые мы здесь рассматривать не будем. Важно знать, что они |
||||||||||||
существуют. |
|
|
|
|
|
|
|
|
|
|
|
|
Теперь перейдем к численным методам приближенного решения |
||||||||||||
дифференциального уравнения первого порядка. Численно решить |
||||||||||||
дифференциальное уравнение |
|
|
|
|
|
|
|
|
|
|||
|
|
|
y′ = f (x, y), |
y(x0 ) = y0 |
|
|
|
|
|
|
||
это значит, что |
для заданной последовательности аргументов |
x1, x2 ,K, xn |
||||||||||
найти такие значения |
y1, y2 ,K, yn , что |
yk |
≈ y(xk ) , |
k = 1, 2,K, n , |
|
где |
y(x) |
|||||
искомое решение уравнения. |
|
|
|
|
|
|
|
|
|
|||
Рассмотрим один из самых простых численных методов |
– |
метод |
||||||||||
Эйлера. Идеи, положенные в его основу, являются исходными для ряда |
||||||||||||
других, более точных методов. |
Пусть требуется найти решение уравнения |
|||||||||||
на отрезке |
[x0 , x0 + H |
]. Разобьём отрезок на n равных частей и получим |
||||||||||
последовательность точек |
|
|
|
|
|
|
|
|
|
|||
23
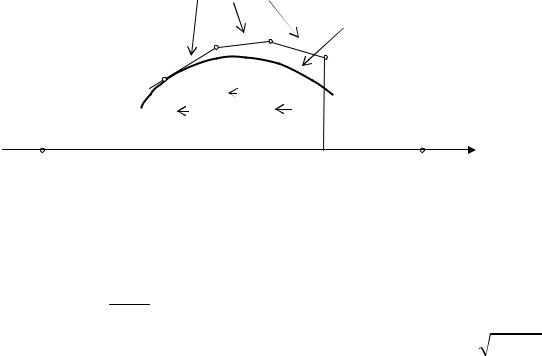
xk = x0 + kh, k = 0,1,K, |
n −1, |
h = H / n . |
В точке (x0 , y0 ) известно направление |
поля |
f (x0 , y0 ) , т.е. угловой |
коэффициент касательной к неизвестной интегральной кривой. Поэтому из
уравнения касательной в этой точке y − y0 = f (x0 , y0 )(x − x0 ) |
мы можем |
||
получить приближённое значение ординаты y1 ≈ y(x1 ) |
искомой |
кривой |
|
(см. рис. 42.2) |
|
|
|
y1 = y0 + f (x0 , y0 )(x1 − x0 ) = y0 + f (x0 , y0 )h . |
|
|
|
В точке (x1, y1 ) нам опять известно направление поля |
f (x1, y1 ) |
и |
можно |
вычислить y2 ≈ y(x2 ) |
|
|
|
y2 = y1 + f (x1, y1 )h . |
|
|
|
Таким образом, приближённо искомая интегральная кривая заменяется ломаной и приближённые значения искомого решения вычисляются по формуле
yk = yk −1 + f (xk −1, yk −1 )h .
Решение уравнения представляется в виде таблицы с шагом аргумента h
График прибл. реш.
Точное
|
|
y0 |
|
y1 |
y2 |
|
|
|
|||
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
x0 |
x1 |
|
x2 |
||
Рис. 42.2
Пример. Методом Эйлера на отрезке [ 0;0,8 ] получить решение
уравнения y′ = y + x , y(0) = 1. y − x
На рис. 42.3 приведен график точного решения y(x) = x + 
 2x2 + 1 , которое можно получить, решив уравнение как однородное (решите!), а
2x2 + 1 , которое можно получить, решив уравнение как однородное (решите!), а
также графики приближённых решений, |
вычисленные с шагом h = 0, 2 |
(нижняя ломаная) и h = 0,1 (средняя |
кривая) соответственно. Для |
24 |
|
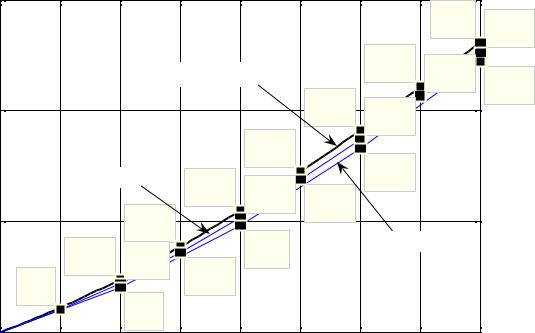
сравнения приведены также значения точного и приближённых решений в соответствующих точках.
2.5
|
|
|
X: 0.8 |
X: 0.8 |
|
|
|
Y: 2.31 |
|
|
|
|
Y: 2.269 |
|
|
|
|
|
|
|
|
X: 0.7 |
X: 0.7 |
|
y=x+sqrt(2x2+1) |
|
Y: 2.107 |
X: 0.8 |
|
|
Y: 2.066 |
|||
|
X: 0.6 |
|
|
Y: 2.224 |
2 |
X: 0.6 |
|
|
|
Y: 1.911 |
|
|
||
|
|
Y: 1.872 |
|
|
|
|
|
|
|
X: 0.5 |
|
|
|
|
|
|
|
|
|
Y: 1.725 |
|
X: 0.6 |
|
|
|
|
h=0.1 |
|
|
|
|
|
||
|
|
X: 0.4 |
X: 0.4 |
|
Y: 1.828 |
|
|
||
|
|
|
|
Y: 1.549 |
X: 0.5 |
|
|
|
|
|
|
|
|
Y: 1.516 |
|
|
|
||
|
|
|
|
|
Y: 1.688 |
|
|
|
|
1.5 |
|
|
X: 0.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Y: 1.386 |
|
|
|
|
|
|
|
|
|
|
|
X: 0.4 |
|
h=0.2 |
|
||
|
|
X: 0.2 |
X: 0.2 |
|
|
|
|||
|
|
|
Y: 1.48 |
|
|
|
|
||
|
Y: 1.239 |
|
|
|
|
|
|||
|
Y: 1.22 |
X: 0.3 |
|
|
|
|
|
||
|
X: 0.1 |
|
|
|
|
|
|
||
|
|
|
Y: 1.359 |
|
|
|
|
|
|
|
Y: 1.1 |
|
|
|
|
|
|
|
|
|
|
X: 0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y: 1.2 |
|
|
|
|
|
|
1 |
0.1 |
|
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0 |
|
||||||||
Рис. 42.3
25

Лекция 43. Дифференциальные уравнения второго порядка
43.1. Задача Коши. Перейдем теперь к изучению дифференциального уравнения второго порядка. Общий вид этого уравнения следующий
′ |
′′ |
(43.1) |
F (x, y, y , y |
) = 0 . |
Если из этого уравнения можно выразить старшую производную как функцию остальных переменных
y |
′′ |
= |
′ |
(43.2) |
|
f (x, y, y ) , |
то такое его представление называют формой Коши.
Общее решение уравнения второго порядка содержит две произвольные постоянные. Например, уравнение y′′ = x легко решается
путем повторного интегрирования
y′ = x + C1 , y = x2 + C1x + C2 .
2
Для выделения частного решения требуется задать два условия. Один из возможных вариантов их задания представляет собой задачу Коши,
состоящую в нахождении решения |
y(x) , удовлетворяющего |
заданным |
|
начальным условиям |
|
|
|
y(x0 ) = y0 , |
′ |
(43.3) |
|
y |
(x0 ) = y1 . |
||
Геометрически они означают, что интегральная кривая проходит через заданную точку ( x0 , y0 ) и касательная к интегральной кривой в этой
точке имеет заданный угловой коэффициент y1 . Условия существования и
единственности решения задачи Коши формулируются в следующей теореме.
Теорема Коши. Пусть функции f (x, y, y′) , f y′(x, y, y′) и f y′′ ( x, y, y′) непрерывны в некоторой окрестности точки (x0 , y0 , y1 ) трехмерного
пространства. Тогда существует и единственно решение уравнения (43.2), удовлетворяющее начальным условиям (43.3).
В отличие от дифференциального уравнения первого порядка, для которого при выполнении условий теоремы Коши интегральные кривые не пересекались на плоскости ( x, y) , для дифференциального уравнения
второго |
порядка |
они, |
вообще |
говоря, |
пересекаются в |
этой |
плоскости. |
Однако, |
если |
рассмотреть |
кривые |
′ |
в |
трехмерном |
|
(x, y(x), y (x)) |
|||||||
|
|
′ |
то согласно теореме Коши они не пересекаются. |
||||
пространстве (x, y, y ) , |
|||||||
|
|
|
|
26 |
|
|
|
43.2. Задача о цепной линии. Прежде, чем перейти к изложению некоторых методов решения дифференциальных уравнений второго порядка, рассмотрим задачу о так называемой цепной линии: какую форму принимает под действием силы тяжести однородная гибкая нерастяжимая тяжёлая нить с закреплёнными концами?
Эта задача возникла очень давно. Леонардо да Винчи (1452-1519) считал, что нить примет форму дуги окружности (если стрела прогиба нити невелика), а голландский математик Альбер Жирар (1595-1633) высказал предположение, что нить примет форму параболы. Получим дифференциальное уравнение, решением которого и будет функция, описывающая форму цепной линии. Выберем систему координат как на рис. 43.1.
y
R
T
α
B 
R
H
A
o
x
|
Рис. 43.1 |
|
|
Рассмотрим часть кривой |
AB так, что касательная в точке |
A |
|
горизонтальна. На неё действуют следующие силы: в точке |
A |
– |
|
горизонтальное натяжение H , в точке B – направленное по касательной |
|||
натяжение T и вес части нити |
AB , пропорциональный её длине. Вес |
||
участка AB равен · , где p – |
вес единицы длины нити, а s – |
длина |
|
дуги AB . Согласно условиям равновесия сумма проекций вертикальных и горизонтальных составляющих всех сил должна быть равной нулю. Поэтому получаем
|
T cos α = H |
|
. |
T sin a = p × s
Разделив второе равенство на первое, находим
′ |
|
dy |
|
p × s |
|
|
= = |
. |
|||||
tgα = yx |
||||||
|
|
dx |
H |
|||
27 |
|
|
|
|
||
Наша задача свелась к решению этого дифференциального уравнения.
Для того чтобы исключить переменную |
|
|
|
s , продифференцируем его по |
|||||||||||||||||||||||||||||||||||||||
переменной x . В итоге получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
′′ |
= |
|
|
|
p d s |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
yxx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H d x |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds = |
|
|
|
|
dx , |
|
|
||||||||||||||
Так как дифференциал дуги равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + y′2 |
то получим |
||||||||||||||||||||||||||||
дифференциальное уравнение второго порядка |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y′′ = |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + y′2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решим его, понизив порядок уравнения. |
|
|
|
Введем новую переменную z , |
|||||||||||||||||||||||||||||||||||||||
обозначив |
y′( x) = z( x) , и пусть, для краткости, |
|
p |
= |
1 |
. Тогда уравнение |
|||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
a |
|
|
|||
примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
dz |
= |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + z2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
«Разделим» переменные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
= |
1 |
dx . |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
1 + z2 |
|
|
|
|
a |
|
|
|
|
|
|
|
|
||||||||||||||||||||
Интегрируя, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
x |
+ C . |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
ln |
z + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
1 + z2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из условия, что при x = |
0 |
′ |
|
|
|
|
|
|
|
|
|
= 0 (см. рис. 43.1), следует C = 0 . |
|||||||||||||||||||||||||||||||
y |
(0) = z(0) |
||||||||||||||||||||||||||||||||||||||||||
Таким образом, имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
z + |
|
1 + z2 = ex a . |
|
|
|
|
|
|
(43.4) |
||||||||||||||||||||||||||||||
Для того чтобы выразить z , умножим обе части этого равенства на |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
−1 = (z − |
|
|
|
|
|
z − |
|
= −e− x a . |
|||||||||||||||||||||||||||||||
z − |
|
|
|
1 + z2 |
) ex a |
|
|
|
|
|
1 + z |
||||||||||||||||||||||||||||||||
1 + z2 |
и получим |
или |
|
|
|||||||||||||||||||||||||||||||||||||||
Сложив (43.4) с последним равенством, приходим к дифференциальному уравнению первого порядка
z = y′ = 12 (ex a − e−x
a − e−x a ).
a ).
Интегрируя, находим |
y = |
a |
(ex a + e−x a ) + C . |
|
|||
|
2 |
1 |
|
|
|
||
28
8 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
-5 |
||||||||||
|
|
|
|
|
|
Рис. 43.2 |
|
|
|
|
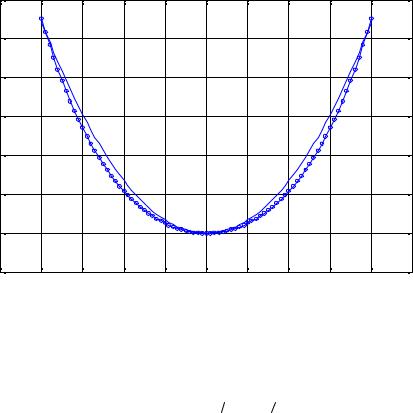
Ясно, что любая кривая этого семейства имеет одну и ту же форму цепной линии
2 |
( |
|
) |
|
a |
||
y = |
a |
|
ex a + e− x a |
|
= a ch |
x |
. |
|
|
|
|
||||
На рис. 43.2 эта кривая приведена для сравнения вместе с параболой. Таким образом, оказывается, что нить принимает форму
гиперболического косинуса. В оправдание выдающихся ученых, занимающихся этой задачей, стоит сказать, что в то время ещё не было показательной функции с основанием e ≈ 2,71828... . Задачу о провисающей верёвке решил в 1697г. оксфордский астроном и математик Д. Грегори (1661-1708).
43.3. Методы понижения порядка уравнения. Для решения задачи о цепной линии был использован метод, который применяется для дифференциальных уравнений второго порядка вида
y |
′′ |
|
|
′ |
|
|
|
= f (x, y ) , |
|
||||
не содержащего явно переменной |
y . |
|
|
|||
Другой метод относится к уравнениям, не содержащим явно |
||||||
независимой переменной x , т.е. |
|
|
|
|
||
|
|
y |
′′ |
= f |
′ |
(43.5) |
|
|
|
( y, y ) . |
|||
29

Введем новую функцию p = p( y) так, чтобы выполнялось y′(x) = p( y(x)) . При этом предполагается, что y(x) ¹ const , так как в этом случае этот
метод не применим (поэтому наличие таких решений нужно проверять отдельно). Найдем
y′′ = dp dy = dp p . dy dx dy
Тогда уравнение (43.5) сводится к уравнению первого порядка
dp p = f ( y, p) dy
относительно неизвестной функции p = p( y) . Пусть p = p( y,C1 ) – его
общее решение. Возвращаясь к исходной переменной, получим дифференциальное уравнение первого порядка
dy = p( y,C1 ) dx
с разделяющимися переменными, решая которое, окончательно найдем общее решение уравнения (43.5)
dy
∫ p( y,C1 ) = x + C2 .
Заметим, что решение получилось как зависимость x = x( y,C1,C2 ) .
30
