
9397
.pdfточнее объём «ступенчатого» тела будет соответствовать тому числу, которое следует считать объёмом тела G . За точное значение объёма естественно принять предел сумм (49.1) при неограниченном увеличении числа подобластей Di . Переходя к пределу при n → ∞ , потребуем, чтобы
все частичные области стягивались в точку. Для этого введём понятие диаметра области Di как наибольшего расстояния между её точками.
Диаметром разбиения называется наибольший из диаметров областей Di . Обозначим его dn .
Будем считать теперь по определению, что объём тела G есть предел, если он существует, к которому стремится сумма (49.1) при диаметре разбиения, стремящемся к нулю
n |
|
V = lim ∑ f (xi , yi ) Si . |
|
dn →0 i=1 |
|
49.2. Определение двойного |
интеграла. Чтобы ввести |
математическое понятие двойного интеграла функции f ( x, y) по области
D , будем сохранять способ рассуждений, использовавшийся для определения объёма цилиндрического тела.
Рассмотрим в плоскости xOу область D , ограниченную замкнутой
линией L без самопересечений, причём точки, лежащие на границе, будем считать принадлежащими области. Такие области называются
замкнутыми. |
Пусть в |
области D задана функция f ( x, y) . |
Разобьём |
||
область |
на |
|
n частей |
D1, D2 , ..., Dn . В каждой подобласти Di |
выберем |
точку Pi ( xi , yi ) и сформируем так называемую интегральную сумму |
|||||
|
|
|
|
n |
|
|
|
|
|
I n = ∑ f ( xi , yi ) S i , |
|
|
|
|
|
i =1 |
|
где f ( x , y |
) – |
значение функции в точке Pi , а Si – площадь области D . |
|||
i |
i |
|
|
|
i |
Рассмотрим произвольную последовательность интегральных сумм, составленных для функции f ( x, y) в области D при различных
способах разбиения её на части. Будем предполагать, что диаметр разбиения стремится к нулю при n → ∞ .
Если существует предел интегральных сумм In при диаметре разбиения, стремящемся к нулю, и этот предел не зависит ни от способов разбиения области D на подобласти D1, D2 , ..., Dn , ни от выбора точек Pi в каждой подобласти Di , то этот предел называется двойным интегралом функции f ( x, y) по области D и обозначается
∫∫ f ( x, y)ds .
D
Функция f ( x, y) в этом случае называется интегрируемой в области D ; область D называется областью интегрирования.
61
Используем независимость предела интегральных сумм для интегрируемой функции от способа разбиения исходной области на
подобласти. Мы можем разбить область |
D на части прямыми линиями, |
||||
параллельными координатным осям ( x = const и y = const ). |
При этом |
||||
площадь |
области |
Di выражается |
через |
приращения |
координат |
Si = xi |
yi , а интегральная сумма приобретает вид |
|
|||
|
|
n |
|
yi . |
|
|
|
I n = ∑ f ( xi , yi ) xi |
|
||
|
|
i =1 |
|
|
|
Поэтому для двойного интеграла в декартовых координатах используется ещё одно обозначение
∫∫ f ( x, y)dxdy .
D
Достаточным условием существования двойного интеграла является непрерывность функции f (x, y) в области D , граница которой
представляет собой кусочно-непрерывную кривую.
Пользуясь рассуждениями предыдущего параграфа, мы приходим к геометрическому смыслу двойного интеграла. Он состоит в том, что для функции z = f (x, y) ³ 0 двойной интеграл равен объёму V цилиндрического тела, ограниченного поверхностью z = f ( x, y) . Итак,
V = ∫∫ f ( x, y)ds .
D
Если же функция z = f (x, y) ≤ 0 , то V = − ∫∫ f ( x, y)ds
D
Рис. 49.3
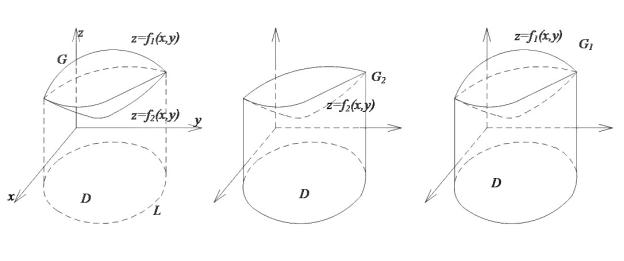
Полученный результат можно использовать для вычисления объёма
тела, ограниченного двумя поверхностями. |
Пусть тело |
G ограничено |
|
сверху поверхностью |
z = f1 ( x, y ) ³ 0 , |
снизу – |
поверхностью |
z = f 2 ( x , y ) ³ 0 , причём |
проекцией обеих |
поверхностей |
на плоскость |
xOу является область D (рис. 49.3).
62
Объём такого тела равен разности объёмов двух цилиндрических тел
V = ∫∫ f1 (x, y)dxdy - ∫∫ f2 (x, y)dxdy .
D |
|
D |
|
|
Формула верна не только |
для |
неотрицательных функций |
f1 ( x, y) |
и |
f 2 ( x, y) , но для любых |
непрерывных функций |
f1 и |
f2 , |
|
удовлетворяющих условию |
f1 (x, y) ³ f2 (x, y) . |
|
|
|
49.3. Свойства двойного интеграла. Поскольку двойной интеграл вводится по той же схеме, по которой вводился определённый интеграл функции одной переменной на отрезке, то свойства этих интегралов аналогичны. Они вытекают из рассмотрения соответствующих интегральных сумм. В частности, двойной интеграл суммы двух (или любого конечного числа) функций по области D равен сумме двойных интегралов по этой области каждой из функций в отдельности
∫∫( f (x, y)+ g(x, y))dxdy = ∫∫ f (x, y)dxdy + ∫∫ g(x, y)dxdy .
D D D
Постоянный множитель можно выносить за знак двойного интеграла, т.е. при c = const верно равенство
∫∫cf (x, y)dxdy = c∫∫ f (x, y)dxdy .
D D
Если область D разбита на конечное число областей D1 , D 2 , ..., D n без общих внутренних точек, то
|
|
n |
|
|
|
∫∫ f (x, y)dxdy = ∑ ∫∫ f (x, y)dxdy . |
|||
|
D |
i =1 |
D |
|
|
|
|
i |
|
Если |
f (x, y) ³ g (x, y) |
в области |
D , то |
для интегралов верно |
аналогичное неравенство |
|
|
|
|
|
∫∫ f (x, y)dxdy ³ ∫∫ g(x, y)dxdy . |
|||
|
D |
D |
|
|
Если |
в качестве подынтегральной |
функции |
рассмотреть функцию, |
|
тождественно равную единице ( f (x, y) ≡ 1) , то в интегральной сумме все слагаемые будут представлять площади частичных областей
n |
|
|
|
I n = ∑ 1 × D S i = S . |
|
|
|
i = |
1 |
|
|
Видим, что интегральная сумма при любом n |
в этом случае |
равна |
|
площади области S . Таким же, |
естественно, |
оказывается и |
предел |
|
63 |
|
|

интегральных сумм. Тем самым, получаем способ вычисления площади плоской области D с помощью двойного интеграла
∫∫1d x d y = S .
D
Из последних двух свойств вытекает, что если m ≤ f ( x, y) ≤ M в области D , то
m S ≤ ∫∫ f ( x , y ) d x d y ≤ M S .
D
Это даёт оценку отношения двойного интеграла к площади области
m ≤ S1 ∫∫D f ( x, y )d xd y ≤ M .
Введём понятие среднего значения функции f (x, y) в области D
f ср = S1 ∫∫D f ( x , y ) d x d y .
Его геометрическая интерпретация состоит в следующем. Если дана
функция z = f ( x, y) ³ 0 |
в области D , |
то объём цилиндрического |
тела, |
|
ограниченного сверху |
поверхностью |
z = f ( x, y ) , равен |
произведению |
|
площади его основания на среднее значение функции V |
= f ср × S . Тем |
|||
самым, f с р является высотой прямого цилиндра с основанием D , |
объём |
|||
которого равен объему исходного цилиндрического тела.
Поскольку функция, непрерывная в замкнутой и ограниченной области D , принимает все свои промежуточные значения между наименьшим и наибольшим, то в этой области найдётся точка ( ξ , η ) , в которой достигается среднее значение функции, т.е.
∫∫ f ( x, y)dxdy = f (ξ, η) S .
D
Последнее свойство является аналогом теоремы о среднем значении для определённого интеграла функции одной переменной.
64

Лекция 50. Вычисление двойного интеграла в декартовых
иполярных координатах
50.1.Вычисление двойного интеграла в прямоугольных декартовых координатах. Чтобы вычислить двойной интеграл, следуя введенному выше определению, мы должны были бы находить предел интегральных сумм, доказывая при этом его независимость от разбиения области и выбора точек в каждой подобласти. Такой способ при необходимости применяется в приближенных вычислениях двойных интегралов. Однако, подобно тому, как определенный интеграл по отрезку, являющийся пределом соответствующих интегральных сумм, находится с помощью формулы Ньютона-Лейбница, двойной интеграл может быть вычислен путем двух операций последовательного интегрирования.
Для этого нужно, прежде всего, точно описать область, по которой ведётся интегрирование. Область D назовем правильной в направлении
оси Oy , если |
существуют две непрерывные на отрезке |
[ a , b ] |
функции |
|||||||
y = ϕ1( x) |
и |
y = ϕ2 (x) , |
такие, |
что для |
всех точек |
( x , y ) области |
||||
выполняются |
условия |
ϕ1(x) ≤ y ≤ ϕ2 (x) . |
Иными |
словами, |
область |
|||||
ограничена графиками |
указанных функций y = ϕ1( x) |
и y = ϕ2 (x) , а также, |
||||||||
быть может, прямыми |
x = a |
и x = b . |
|
|
|
|
||||
Область называется правильной в направлении оси Ox , если |
||||||||||
существуют |
непрерывные |
на |
отрезке |
[c, d ] функции |
x = ψ1 ( y) и |
|||||
x = ψ2 ( y ) |
(см. рис. 50.1) такие, что ψ1 ( y ) ≤ ψ 2 ( y ) , |
и для точек области |
||||||||
выполняются условия c ≤ y ≤ d , ψ1 ( y) ≤ x ≤ ψ2 ( y) .
Это означает, что для правильной в направлении оси Oy (Ox) области всякая прямая, параллельная оси Oy (Ox) и проходящая через
внутреннюю точку области, пересекает границу области ровно в двух точках.
На рис. 50.1 изображены области, правильные в направлении обеих осей.
65
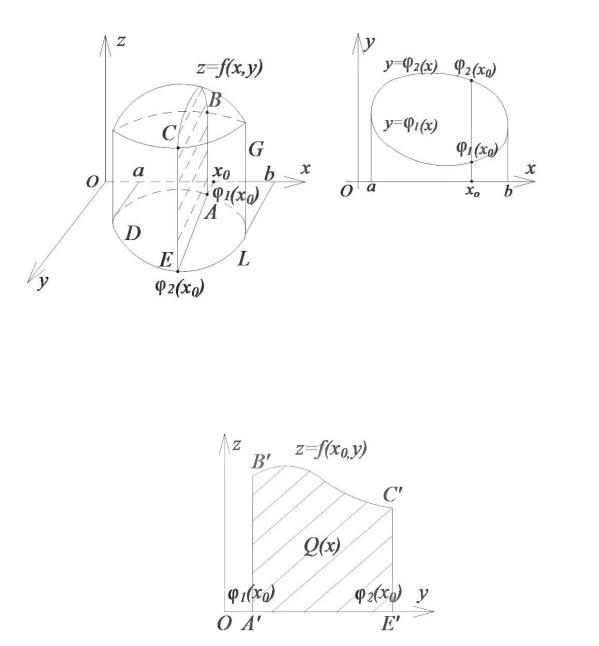
Рис. 50.1
Пусть z = f ( x, y ) ³ 0 – непрерывная на этой области функция. Напомним, что объём тела можно вычислить как интеграл от площадей его плоских сечений. А именно, если для каждого x [a,b] известна площадь S (x) сечения тела плоскостью, перпендикулярной оси Ox , то его объём
b
выражаетcя формулой V = ∫ S ( x)d x .
a
Используем эту формулу для вычисления двойного интеграла, помня, что он равен объёму цилиндрического тела. Сечение цилиндрического тела плоскостью x = x0 представляет собой криволинейную трапецию ABCE
(рис. 50.2).
Рис. 50.2
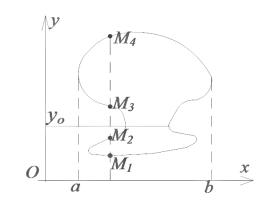
Если эту трапецию спроецировать параллельно оси Ox на плоскость
zOу , то получится трапеция |
′ ′ ′ ′ |
(рис. 50.3), для точек которой |
A B C E |
||
выполняются условия ϕ1(x0 ) ≤ y ≤ ϕ2 (x0 ), |
0 ≤ z ≤ f (x0 , y) . |
|
Рис. 50.3
66
|
|
ϕ |
2 ( x 0 ) |
|
Площадь такой трапеции равна |
S ( x 0 ) = |
∫ f ( x 0 , y ) d y . |
|
|
|
|
ϕ |
1 ( x 0 ) |
|
Таким образом, имеем |
|
ϕ2 ( x ) |
|
|
|
b |
|
|
|
∫∫ f (x, y)dxdy = ∫ dx |
∫ f ( x, y)dy . |
(50.1) |
||
D |
a |
ϕ1 ( x ) |
|
|
Интеграл в правой части формулы (50.1) носит название повторного интеграла. Для его нахождения сначала вычисляется внутренний интеграл
по переменной y в предположении, что x |
– постоянная величина. |
Затем |
|
полученный результат интегрируется по |
переменной |
x – то |
есть |
вычисляется внешний интеграл. Для таких областей используется порядок интегрирования, при котором внешним является интеграл по переменной y . Рассуждая так же, как для областей, правильных в направлении оси Oy
,но, рассекая цилиндрическое тело |
плоскостью y = y0 |
(рис. 50.4), |
|
получим формулу |
|
|
|
∫∫ f (x, y)dxdy = |
d |
ψ2 ( y) |
|
∫ dy |
∫ f ( x, y)dx . |
(50.2) |
|
D |
c |
ψ1( y) |
|
|
|
||
Если область D не является правильной в выбранном направлении, то её разбивают на правильные области. Например, область на рис. 50.4 разбита прямой y = y0 на области D1 и D2 , являющиеся правильными
в направлении оси Oy .
Рис. 50.4
Если область D является прямоугольником со сторонами, параллельными осям координат, для координат точек которого
выполняются неравенства |
a ≤ x ≤ b, c ≤ y ≤ d , то формула (50.1) |
|
приобретает вид |
|
|
|
b |
d |
∫∫ f (x, y)dxdy = ∫dx∫ f (x, y)dy . |
||
D |
a |
c |
|
67 |
|

Заметим, что внешние пределы в повторном интеграле всегда постоянны, а во внутреннем интегррале пределы бывают постоянными числами только в том случае, если D – прямоугольник.
Рассмотрим для примера вычисление с помощью двоойного интеграла объема тела, ограничеенного гиперболическим параболоиддом z = xy
цилиндром, y = x2 и плоскостью y = x (рис. 50.5).
Рис. 50.5
Как видим, область D является правильной в направлении обеих осей, тем самым можно использовать любой порядок интегрирования.
Заменим двойн ой интеграл повторным по формуле (50.1)
|
1 |
x |
∫∫xydxdy = ∫dx ∫ xydy . |
||
D |
0 |
x2 |
Найдём сначала внут ренний интеграл по переменной y , считая
переменную x константой, затем проинтегрируем по x полученную функцию, зависящую уже только от переменной x
1 |
|
x |
|
1 |
|
y 2 |
|
|
x d x = |
1 |
|
|
x 5 |
|
|
1 |
|
|
∫ |
d x |
∫ |
xyd y = |
∫ |
x |
|
|
∫ |
|
x 3 |
− |
d x |
= |
. |
||||
|
|
|
2 |
2 4 |
||||||||||||||
|
|
2 |
|
|
x 2 |
2 |
|
|
|
|
||||||||
0 |
|
x 2 |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Рассмотрим для той же области, изображённой на рисунке 50.5, |
||||||||||||||||||
другой порядок |
инт егрирования. |
В этом |
случае |
у |
внешнего интеграла |
|||||||||||||
пределы останутся прежними, так как в области D переменная y меняется от 0 до 1, а для нахождения функций ψ1( y) и ψ2 ( y) следует выразить x через переменную y из уравнений линий, ограничивающих D . По формуле (50.2) получается, что
68

|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
y |
|
|
|
||||||||
|
|
|
∫ dx ∫ xydy = ∫ dy ∫ xydx . |
|
|
|
|||||||||||||
|
|
|
0 |
x2 |
0 |
y |
|
|
|
||||||||||
Теперь внутренний интеграл берётся по переменной |
x , а |
внешний – по |
|||||||||||||||||
переменной y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 dy |
|
y |
|
1 |
|
x2 |
|
|
|
|
1 |
y2 |
|
y3 |
dy = |
|
|
||
∫ |
xydx = |
y |
|
|
y dy = |
− |
1 |
|
|||||||||||
∫ |
|
|
|
24 . |
|||||||||||||||
∫ |
|
2 |
|
y |
∫ 2 2 |
|
|||||||||||||
0 |
y |
|
0 |
|
|
|
|
|
|
0 |
|
|
|
||||||
50.2. Вычисление двойного интеграла в полярных координатах.
Все проведённые до сих пор вычисления выполнялись в прямоугольной декартовой системе координат. Использование полярной системы координат даёт возможность упростить вычисление двойного интеграла во многих случаях, например, если область интегриррования является сектором круга или кольца.
Введём на плоскости полярную систему координат, полюс которой совпадает с началом декартовой системы координат, а полярная ось – с осью Ox . В этом случае полярные координаты связаны с декартовыми
соотношениями |
{x = r cos ϕ |
|
|
|
|
|
y = r sin ϕ |
(50.3) |
Эти соотношения позволят перейти в записи уравнений границы области от декартовых координат к полярным.
Пусть в декартовой системе координат задана некоторая область D . Двойной интеграл определялся как предел интегральных сумм. Поскольку этот предел для интегрируемой функции не зависит от способа разбиения исходной области на подобласти, мы можем разрезать оббласть D на части
любым |
|
|
способом. |
Р азобьём область |
|
|
D сетью координатных линий |
|||||||||||||||||||||||||||||||||||||||||||
ϕ = const, r = const |
на |
|
|
|
частей. Рассмотрим одну из частей площадью |
|||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
, расположенную внутри области |
|
|
|
(см. рис. 50.6). Площадь |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
подсчитаем как разность |
|
|
площадей круговых секторов с центральным |
|||||||||||||||||||||||||||||||||||||||||||||||
углом |
|
|
|
|
|
и радиусами |
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
69
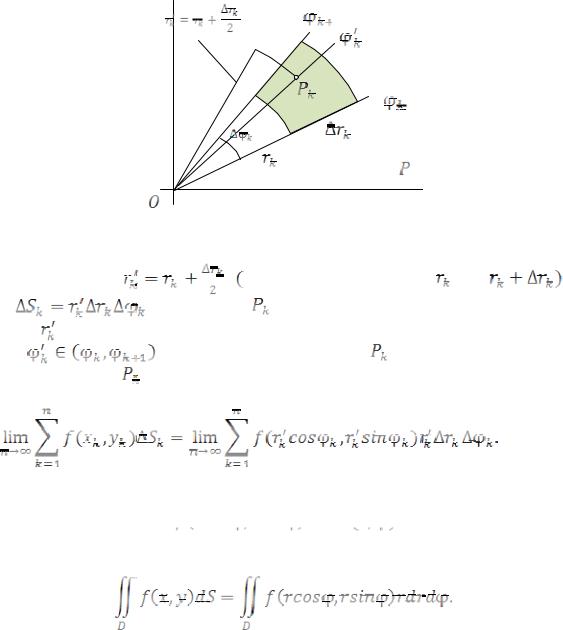
Рис. 50.6 |
Обозначим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
средний радиус между и |
|
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точку |
|
|
|
выберем лежащей на окружности |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
радиуса |
|
|
|
|
|
(мы расп олагаем свободой в выборе промежуточной точки). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
полярный угол точки |
|
|
. В ыражая декартовы |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
координаты точки |
|
|
|
|
|
|
|
через её полярные координаты, получаем |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В правой части последней формулы мы видим предел интегральной суммы для функции 



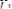































 , поэтому получаем формулу вычисления двойного интеграла в полярных координатах
, поэтому получаем формулу вычисления двойного интеграла в полярных координатах
Коротко можно сказать, что при переходе в дво йном интеграле к
полярным координатам |
подынтегральная |
функция |
в ыражается |
через |
|||
переменные |
r и |
ϕ с |
помощью формул |
(50.3), а |
в ыражение |
dxdy |
|
заменяется на произв едение |
rdrdϕ. |
|
|
|
|||
Вычисление |
дво йного |
интеграла в полярных |
координатах |
также |
|||
производится |
повторным интегрированием, только теперь по переменным |
||||||
r и ϕ . Область интегрирования D должна быть в этом случае правильной по отношению к полярной системе координат (рис. 50.7). Это означает, что
она будет ограничена лучами ϕ = ϕ1 и ϕ = ϕ2 , а также кривыми r = r1 (ϕ) и
то есть для точек области выполнены условия ϕ1 ≤ϕ≤ ϕ2 , r1(ϕ) ≤ r ≤ r2 (ϕ) .
70
