
9397
.pdf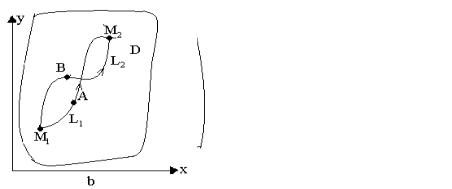
не зависит от кривой, соединяющей точки А и B. 3) Внутри области D выполняется тождество
|
|
′ |
′ |
(x, y) . |
(56.2) |
||
|
|
Py |
(x, y) ≡ Qx |
||||
4) |
Существует |
функция U (x, y) |
, |
называемая |
потенциальной |
||
функцией векторного поля F ( x, y ) = {P ( x, y ), |
Q ( x, y )} , для которой |
||||||
|
′ |
( x, y ) = |
P(x,y) , |
′ |
( x, y ) = Q(x,y) , |
(56.3) |
|
|
U x |
U y |
|||||
или иными словами, для которой полный дифференциал определяется по формуле
dU = P(x, y)dx + Q(x, y)dy . |
(56.4) |
Данную теорему надо понимать следующим образом: если одно из ее утверждений выполняется, то выполняются и все остальные. Поэтому доказать теорему можно по схеме: 1)→ 4)→ 3)→ 2)→ 1), из которой будет следовать эквивалентность всех утверждений. Приведем реализацию лишь последних двух фрагментов этой схемы. Покажем, что из справедливости
3) вытекает 2). |
′ |
′ |
|
|
|
|
Итак, пусть |
( x, y) |
в области D |
и пусть C |
|||
Py |
( x, y) ≡ Qx |
произвольный замкнутый контур без самопересечений, целиком лежащий
в области D, а D1 |
есть область, ограниченная контуром C . По формуле |
||
Грина |
′ |
′ |
(x, y))dxdy = ∫∫0dxdy = 0 . |
|
|||
∫ P(x, y)dx + Q(x, y)dy = ∫∫(Qx |
(x, y) − Py |
||
L |
D1 |
|
D1 |
Таким образом, криволинейный интеграл по любому замкнутому контуру C равен нулю.
Докажем, что из справедливости 2) следует 1). Пусть M1 и M2 любые две точки из области D и пусть L1 и L2 два пути, их соединяющие (рис. 56.1,а).
Рис. 56.1
121
Пусть |
C есть контур M1 AM 2 BM1 . |
По условию интеграл по контуру C |
|||
равен |
нулю. |
Свойства криволинейных интегралов позволяют записать |
|||
цепочку равенств: |
|
|
|
||
|
0 = ∫ Pdx + Q dy = ∫ Pdx + Q dy + |
∫ |
Pdx + Q dy = |
||
|
C |
M 1 AM 2 |
M 2 BM 1 |
|
|
|
|
= ∫ Pdx + Q dy − ∫ Pdx + Q dy , |
|||
|
|
L1 |
L2 |
|
|
откуда и вытекает равенство |
|
|
|
||
|
|
∫ P d x + Q d y = ∫ P d x + Q d y . |
|||
|
|
L1 |
L 2 |
|
|
На рис. 56.1,a рассмотрен случай, |
когда пути |
L1 |
и L2 , соединяющие |
||
точки M1 и M2 |
не пресекаются. В случае, когда эти пути пересекаются, |
||||
вышеприведенное равенство доказывается несколько сложнее (рис. 56.2,б). Пусть функции P( x, y), Q( x, y) таковы, что выполняются условия
выше сформулированной теоремы. Как находить потенциальную функцию U(x, y) , о которой говорится в утверждении 4)? Заметим, что эта задача
является обобщением на двумерный случай задачи о нахождении первообразных для функций от одной переменной.
Будем рассуждать следующим образом. Пусть M0(x0, y0) – некоторая фиксированная точка в области D, а M(x, y) – произвольная точка в области D. В силу теоремы, криволинейный интеграл
∫ P(x, y)dx + Q(x, y)dy
|
M0M |
|
|
|
зависит лишь |
от положения точки |
M(x, y) и, значит, является функцией |
||
переменных x |
и. y. Эту функцию обозначим через U0(x, y) . Итак, |
|
||
|
U 0 (x, y) = ∫ |
P(x, y)dx + Q(x, y)dy. |
(56.5) |
|
|
M 0M |
|
|
|
Если в области D зафиксировать |
другую точку M1 (x1, y1 ) , |
то наши |
||
рассуждения дадут другую функцию: |
|
|
||
|
U1(x, y) = |
∫ |
P(x, y)dx +Q(x, y)dy. |
(56.6) |
M1M
Но по свойствам криволинейного интеграла
U1 (x, y) − U0 (x, y) = ∫ P(x, y)dx + Q(x, y)dy = const,
M0M1
аэто говорит о том, что функции U1 (x, y) и U0 (x, y) отличаются друг от
друга на постоянную величину (также как любые две первообразные для одной и той же функции).
122

Для вычисления значений функции U0 (x, y) можно опять
воспользоваться независимостью криволинейного интеграла от пути интегрирования. Пусть точка M (x, y) лежит в области D. Предположим,
что ломаная M 0 M 1 M (для которой M 0 M 1 параллельна оси OX , а M 1 M
параллельна оси OY ) целиком лежит в области D. В этом случае точка M1 имеет координаты ( x , y 0 ) . При этом вдоль отрезка M 0 M 1 нет
изменения переменной y и потому dy = 0 , а вдоль отрезка M1M нет изменения переменной x и потому dx = 0 . В таком случае будем иметь
U0 (x, y) = ∫ P(x, y)dx + Q(x, y)dy = ∫ P(x, y)dx + Q(x, y)dy +
|
M 0 M1M |
M 0 M1 |
|
x |
y |
+ ∫ P(x, y)dx + Q(x, y)dy = ∫ P(x, y0 )dx + ∫ Q(x, y)dy. |
||
M1M |
x0 |
y0 |
И, следовательно, искомая потенциальная функция может вычисляться по формуле
x |
y |
|
U 0 (x, y) = ∫ P(x, y0 )dx + ∫ Q( x, y)dy . |
(56.7) |
|
x0 |
y0 |
|
Если ломаная М0М1М не лежит целиком в области D, то можно построить ступенчатую ломаную, звенья которой будут параллельны осям координат и которая целиком лежит в области D. Тогда значение функции U0 (x, y)
будет равно сумме интегралов по соответствующим переменным по каждому звену этой ломаной.
Следствие. Из приведенных выше рассуждений становится
понятным, что, если для поля F ( x, y) = {P( x, y), Q( x, y)} существует потенциальная функция U(x, y) , то для любых двух точек A(x1, y1) и B(x2, y2) , лежащих в области D выполняется равенство
∫ P(x,y)dx +Q(x,y)dy =U(B) −U(A) =U(x2, y2) −U(x1, y1) . (56.8)
AB
Оно означает, что работа по перемещению материального тела из одной точки пространства в другую равна разности значений потенциальной функции в конечной и начальной точках перемещения.
Пусть дано силовое поле
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|||
F (x, y) = P(x, y) i+ Q(x, y) j = |
|
|
, |
|
|
|
|
|
2 + y2 |
|
|
+ y2 |
|||
|
|
x |
2 |
. |
|||
x |
|
|
|
|
|
||
123 |
|
|
|
|
|
|
|

Покажем, что это поле потенциальное, найдем потенциальную функцию и
определим работу по перемещению |
материального объекта из точки |
||||||
A(2, 1) в точку B(3, 4) . |
|
|
|
|
|
|
|
Находим |
2xy |
|
|
|
|
|
|
P′ (x, y) = − |
|
и |
′ |
( x, y) = − |
2 xy |
. |
|
|
|
|
|||||
y |
(x2 + y2) |
2 |
|
Qx |
( x 2 + y 2)2 |
||
|
|
|
|
|
|||
Так как эти производные совпадают, то данное поле действительно является потенциальным. Для нахождения потенциальной функции
воспользуемся |
формулой (3.7), |
|
взяв |
в |
качестве точки M0(x0,y0) точку |
||||||
M0(1,1) . Итак, |
U0 |
(x, y) = ∫ x |
dx+ ∫ |
y |
|
dy = |
|
||||
|
|
|
|||||||||
|
|
x |
|
y |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
1 x2 +1 |
1 x2 +y2 |
. |
|||||||
1(ln(x2 |
+1)−ln2)+1(ln(x2 |
+ y2)−ln(x2 +1)) = 1(ln(x2 |
|||||||||
+ y2 )−ln2). |
|||||||||||
2 |
|
2 |
|
|
|
|
|
2 |
|
||
Потенциальная функция определяется с точностью до постоянной величины. Поэтому в качестве потенциальной функции данного силового
поля можно |
взять и функцию U (x, y) = |
1 |
ln(x2 + y2 ) . |
Работу |
W по |
|
|||||
|
2 |
|
|
|
|
перемещению |
материального объекта из точки A(2, 1) в |
точку |
B(3, 4) |
||
определяем теперь как разность потенциалов в этих точках т.е.
W=U(B)−U(A)=U(3,4)−U(2,1) =1ln25−1ln5=1ln5.
2 |
2 |
2 |
56.2. Случай пространственного силового поля. Для |
||
пространственного силового поля |
|
|
F (x, y, z) = {P(x, y, z), Q(x, y, z), R(x, y, z)} |
(56.9) |
|
аналог теоремы, сформулированной в пункте |
55.1, |
звучит следующим |
образом. |
|
|
124
Теорема. Если функции P( x, y, z), Q ( x, y, z ), R( x, y, z ) и частные
производные |
|
|
|
|
|
|
′ |
′ |
′ |
′ |
′ |
′ |
( x, y, z ) |
Py |
( x, y, z ), Pz |
( x, y, z ), Q x |
( x, y, z ), Q z |
( x, y , z ), R x |
( x, y, z ), R y |
|
непрерывны в односвязной пространственной области D, то следующие утверждения эквивалентны:
1) Если замкнутый контур L , целиком лежит в области D, то
∫ P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz = 0.
L
2) Для любых двух точек A и B, целиком лежащих в области D, криволинейный интеграл
∫ P ( x, y, z )dx + Q ( x, y, z )dy + R ( x, y, z )dz
AB
не зависит от кривой, соединяющей точки A и B . 3) Внутри области D выполняются тождества
Py′(x, y,z) ≡Qx′(x, y,z), Pz′(x, y,z) ≡ Rx′, Qz′(x, y,z) ≡Ry′(x, y,z). (56.10)
4) Существует функция U(x, y, z) , называемая потенциальной функцией векторного поля (56.9), для которой
′ |
′ |
′ |
(x, y, z) |
Ux |
(x, y, z) = P(x, y, z) , Uy |
(x, y, z) = Q(x, y, z) , Uz |
= R(x, y, z) , (56.11)
или, иными словами, для которой полный дифференциал определяется по формуле
dU = P( x, y, z) dx + Q( x, y, z) dy + R( x, y, z)dz . (56.12)
Нахождение потенциальной функции по ее полному дифференциалу в пространстве происходит по схеме, аналогичной плоскому случаю.
Пусть M0 (x0 , y0 , z0 ) – |
некоторая фиксированная точка в области D, а |
|
M ( x, y, z) – произвольная точка в области D. Рассмотрим функцию |
||
U0 (x, y, z) = ∫ |
P(x, y,z)dx + Q(x, y,z)dy + R(x, y,z)dz . |
(56.13) |
M 0 M |
|
|
|
125 |
|
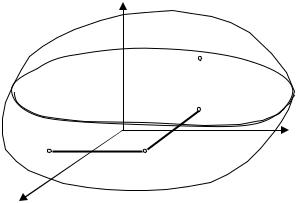
Для вычисления ее значений можно опять воспользоваться независимостью криволинейного интеграла от пути интегрирования.
Соединим точку M (x, y, z) |
ломаной M 0 M 1 M 2 M |
такой, |
что M 0 M1 |
параллельна оси OX , M1M 2 |
параллельна оси OY , |
а M 2 M параллельна |
|
оси OZ . При этом ломаная не выходит за пределы области. |
В этом случае |
||
точка M1 имеет координаты |
(x, y0 , z0 ) , а точка M2 имеет координаты |
||
(x, y,z0) .
Пусть
U0 (x, y, z) = ∫ |
P(x, y,z)dx + Q(x, y,z)dy + R(x, y,z)dz = ∫ |
+ ∫ |
+ ∫ |
M0M1M2M |
M0M1 |
M1M2 |
M2M |
, ,
 , ,
, ,
, ,
, ,
Рис. 56.2
Но, очевидно, что вдоль отрезка M 0 M 1 дифференциалы dy = 0 |
и dz = 0 , |
|||
вдоль отрезка |
M 1M 2 |
дифференциалы dx = 0 |
и dz = 0 , а вдоль отрезка |
|
M 2 M дифференциалы |
dx = 0 и dy = 0 . И потому |
|
||
U 0 ( x, y , z ) = |
x |
y |
z |
|
∫ P ( x, y0 , z0 )dx + ∫ Q ( x, y , z0 )dy + |
∫ R ( x, y, z )dz . |
(56.14) |
||
x0 |
y 0 |
z 0 |
|
|
В качестве конкретного примера рассмотрим поле силы тяжести. На тело массы m вблизи поверхности земли, которую будем считать плоской,
действует направленная вертикально вниз сила тяжести F , величина которой равна mg ( g – ускорение свободного падения).
126
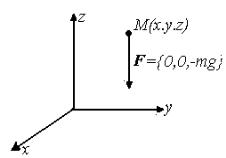
Рис. 56.3
Очевидно, что в данной ситуации
P(x, y, z) = 0, Q(x, y, z = 0, R(x, y, z) = −mg
и условия (56.11) выполнены. Отсюда |
и из формулы (56.14) следует, что |
|||
работа при перемещении материального тела из точки |
M0 (x0 , y0 , z0 ) |
в |
||
точку M(x, y, z) будет равна |
|
|
|
|
|
|
z |
|
|
U0 (x, y, z) = ∫ R(x, y, z)dz = − ∫ |
mgdz = −∫ mgdz = −mg(z − z0 ) . |
|
||
M0M |
M0M |
z0 |
|
|
Эта работа будет положительна, |
если точка M0 выше |
точки M, |
и |
|
отрицательна в противном случае. Потенциальная функция U(x, y,z) принимает вид U (x, y, z) = −mgz + C . Принимая значение этой функции на поверхности земли (z = 0) равным 0, получаем, что потенциалом поля силы тяжести является функция
U(x, y,z) = −mgz.
127
Раздел 11. Ряды
Лекция 57. Ряды
В данном разделе мы познакомимся с математическим обоснованием тех вычислительных процедур, которые реализуются (но которые мы даже не замечаем) при использовании в расчетах значений алгебраических, тригонометрических, и более сложной природы функций. Если до появления компьютеров приходилось обращаться к соответствующим таблицам (не задумываясь о том, как они составлены), то теперь вычисление их значений доверяется компьютерам. Но любой компьютер может выполнять лишь четыре арифметических и несколько простейших логических операций (правда, с очень большой скоростью). Теория рядов раскрывает и обосновывает возможность вычисления значения любой функции с заданной точностью путем выполнения указанных простейших операций.
57.1. Числовые ряды. Основные определения. Пусть имеется бесконечная числовая последовательность
u 1 , u 2 , u 3 ,..., u n ,... .
Если в этой записи везде вместо запятых поставить знак +, то получившаяся запись
u 1 + u 2 |
+ u 3 + ... + u n |
+ ... |
будет называться числовым |
рядом. Числа |
u1 ,u 2 ,... называются |
членами ряда, а un называется |
общим членом ряда (предполагается, что |
|
n принимает в качестве значения любое целое положительное число). Обычно для записи ряда используется сокращение
∞
u1 + u2 + u3 + ... + un + ... = ∑ un . (57.1)
n =1
Так, если имеются следующие четыре последовательности
|
|
|
|
1,1,1,…,1,…. ; |
1,-1,1,-1,….,(-1 |
)n ,..; |
|
||
1, |
1 |
, |
1 |
,..., |
1 |
,... ; a , a q , a q 2 , a q 3 , ..., a q n , ... ( a ¹ 0 ) |
, |
||
|
|
|
|||||||
2 |
3 |
|
n |
|
|
|
|||
то из них можно получить четыре числовых ряда: |
|
|
|||||||
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
1 + 1 + 1 + ... + 1 + ... = ∑1 |
|
(57.2) |
|||
n=1
128
1 −1 + 1 −1... + (−1)n + 1 + ... = |
|
∞ |
|
|
|||||||||
∑(−1)n + 1 |
(57.3) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
1 |
|
1 |
|
1 |
|
1 |
∞ |
|
1 |
|
|
|
1 + |
+ |
+ |
+ ... + |
+ ... = ∑ |
|
, |
(57.4) |
||||||
|
|
|
n |
n |
|||||||||
2 |
3 |
|
4 |
|
n=1 |
|
∞ |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a + aq + aq 2 |
+ aq 3 + ... + aq n |
+ ... = ∑ aq n . |
(57.5) |
||||||||||
n=0
В связи с чем возникает необходимость в рассмотрении такого бесконечного суммирования? Дело в том, что, как будет показано ниже, значения многих функций при каком-то значении аргумента может быть представлено в виде суммы бесконечного числа слагаемых, причем вычисление каждого слагаемого может быть реализовано посредством четырех арифметических операций: сложения, вычитания, умножения и деления. Чтобы понять, как происходит такое представление, наполним формально введенное понятие числового ряда, математическим содержанием, то есть придадим некоторый смысл процедуре сложения бесконечного числа слагаемых. Естественно при этом отталкиваться от изучения поведения сумм конечного, но все возрастающего числа слагаемых, которые мы будем называть частичными суммами ряда.
Итак, пусть дан ряд (57.1) и пусть
|
|
|
|
|
|
n |
|
|
S 1 |
= u 1 ; S2 = u1 + u2 ; |
Sn |
= u1 + u2 + ... + un = ∑uk . |
|
||||
|
|
|
|
|
|
k =1 |
|
|
Величина Sn |
n |
|
|
|
|
|
|
|
= ∑ uk (n = 1,2,...) называется n-ой |
частичной суммой |
|||||||
|
k =1 |
|
|
|
|
|
|
|
данного ряда. Если последовательность |
u 1 , u 2 ,..., |
u n ,... определена, то |
||||||
определена и последовательность частичных сумм S 1 , S 2 ,..., |
S n ,... |
. Если |
||||||
при этом существует конечное число S такое, что |
|
lim S n |
= S , |
то ряд |
||||
|
|
|
|
|
|
n → ∞ |
|
|
(1) называется сходящимся, число S называется его суммой и этот факт |
||||||||
|
|
∞ |
|
|
|
|
|
|
записывается так |
∑ u n = S . Если |
указанного |
конечного |
предела не |
||||
|
|
n =1 |
|
|
|
|
|
|
существует, то ряд (1) называется расходящимся. |
|
|
|
|
||||
Проанализируем приведенные выше примеры (57.2) – (57.5) с точки |
||||||||
зрения введенного |
определения. |
Рассмотрим |
ряд (57.2). Для него |
|||||
последовательность |
частичных |
сумм S1 , |
S2 ,..., S n …. выглядит |
|
следующим образом: |
|
= 1 , |
|
= n …. |
|
S1 |
S2 = 2 ,..., Sn |
||
Очевидно, что lim Sn |
= +∞ |
и, следовательно, ряд (2) расходящийся. |
||
n→∞
Рассмотрим ряд (57.3). Для него последовательность частичных сумм выглядит следующим образом:
129
|
|
|
|
|
|
|
S1 = 1 , |
S2 = 0 , S3 |
= 1, S4 |
= 0 ,..., S 2 n −1 = 1 , S2 n = 0 . |
||||||||||||||||||
Очевидно, что эта последовательность |
предела не имеет и потому ряд |
|||||||||||||||||||||||||||
(57.3) расходящийся. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Рассмотрим ряд (57.5). Его члены представляют геометрическую |
|||||||||||||||||||||||||||
прогрессию с первым членом |
u1 = a |
и знаменателем q . При q=1 ряд |
||||||||||||||||||||||||||
расходится. |
|
При |
q ¹ 1 по формуле |
суммы членов геометрической |
||||||||||||||||||||||||
прогрессии |
|
|
|
|
|
|
a (1 − q n ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
S = |
= |
|
a |
|
− |
aq n |
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− q |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
1 − q |
|
1 − q |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
|
q |
|
|
< 1 |
|
qn → 0 и, следовательно, ряд (5) сходится и его сумма |
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
S = lim |
S |
|
= |
|
|
a |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
− q . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|
1 |
||||||||||||
При |
|
q |
|
> 1 |
|
q |
|
n → +∞ и, поэтому при |
|
q |
|
> 1 ряд (5) расходится. |
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
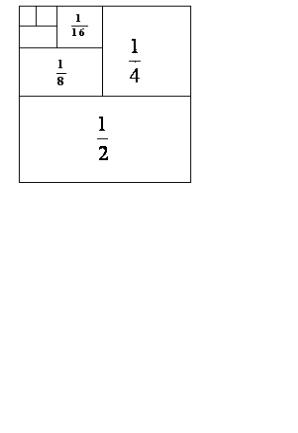
|
При |
a = 1 2 |
и q = 1 2 |
сумма |
S |
|
принимает значение 1 и этот |
|||||||||||||||||||||
факт становится наглядно очевидным из Рис. 57.1. На нем представлен квадрат со стороной равной единице длины. Будем представлять первый член суммы как площадь половины этого квадрата, второй – как площадь четверти квадрата и т.д. Интуитивно ясно, что сумма
S |
|
= |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
... + |
1 |
n |
|
|
|
|
2n |
||||||
|
2 |
4 |
8 |
16 |
|
||||||
|
|
|
|||||||||
«исчерпает» при n → ∞ всю площадь квадрата, т.е. lim Sn = 1.
n → ∞
Рис. 57.1
Рассмотрим теперь ряд (57.4). Он называется гармоническим рядом. Чтобы понять поведение частичных сумм S1 , S 2 ,..., ,... этого ряда,
рассмотрим другой ряд :
1 |
+ |
1 |
|
+ |
1 |
|
+ |
1 |
|
+ |
1 |
|
+ |
1 |
|
+ |
1 |
|
+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+...+ |
1 |
+... |
||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
2 |
4 |
8 |
8 |
8 |
8 |
16 |
16 |
16 |
16 |
16 |
16 |
16 |
16 |
16 |
32 |
32 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
130 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
