
9395
.pdf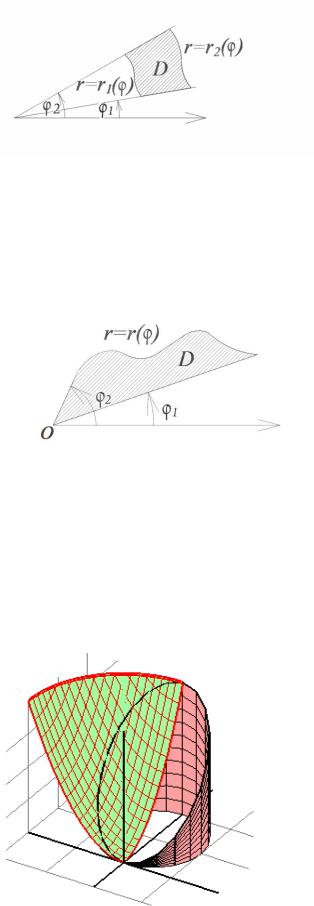
Рис. 50.7
Внешний интегр ал берётся по переменной ϕ , и формула замены двойного интеграла повторным в полярных координатах выглядит следующим образом:
|
ϕ2 |
r2 (ϕ) |
∫∫ f (r co sϕ,r sin ϕ) rdrdϕ = ∫ dϕ |
∫ f (r cosϕ,r sin ϕ) rdr . |
|
D |
ϕ1 |
r1(ϕ) |
Рис. 50.8
Если полюс принадлежит области интегрирования (рис. 50.8), то в этой
формуле r1 (ϕ) = 0 . |
|
|
Вычислим для примера |
объем тела, |
ограниченно го параболоидом |
z = x2 + y 2 , плоскост ью xOy и цилиндром |
x2 + y2 = 2Rx , направляющей |
|
которого служит ок ружность |
радиуса R с |
центром в точке(R,0) (рис. |
50.9). |
|
|
Рис. 50.9
71
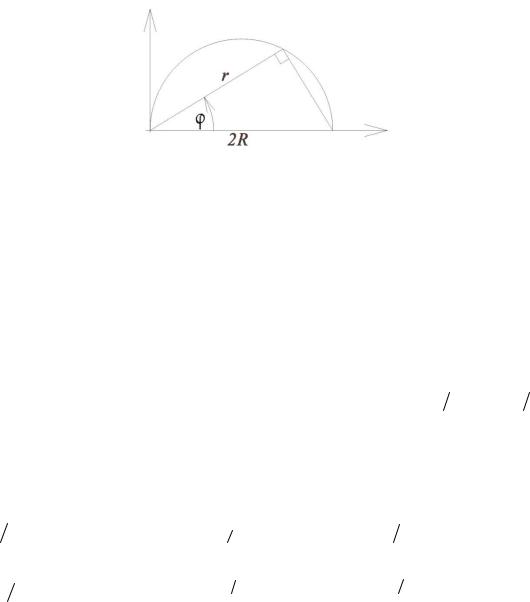
Рис. 50.10
Из геометрических соображений ясно, что полярные координаты точек окружности связаны в этом случае соотношением r = 2R cos ϕ (рис. 50.10). К такому же выводу мы придём, если запишем сначала уравнение
заданной окружности в декартовых координатах x2 + y2 = 2Rx , |
а затем |
подставим в него соотношения (50.3) и выразим переменную r |
через ϕ . |
Именно такой способ получения уравнения линии в полярных координатах
чаще всего используется в конкретных задачах. |
|
|
|
|
|
|
|
|
|
|
||||||||
Итак, область D , |
являющаяся основанием рассматриваемого тела, |
|||||||||||||||||
задаётся |
в полярных |
координатах |
условиями |
− π 2 ≤ ϕ ≤ π 2 , |
||||||||||||||
0 ≤ r ≤ 2Rcosϕ , поэтому объем тела вычисляем следующим образом |
||||||||||||||||||
∫∫ ( x 2 + y 2 ) d x d y = ∫∫ ( r 2 c o s 2 ϕ + r 2 s i n 2 ϕ ) r d r d ϕ = |
|
|||||||||||||||||
D |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
π 2 |
2 R cos ϕ |
|
|
|
π 2 |
|
|
|
|
|
|
|
π 2 |
|
1 + cos 2ϕ 2 |
|||
= ∫ d ϕ |
∫ |
r 3 dr = 4 R 4 ∫ cos4 ϕd ϕ = 4 R 4 |
|
∫ |
|
|
|
d ϕ = |
||||||||||
2 |
||||||||||||||||||
− π 2 |
0 |
|
|
|
− π 2 |
|
|
|
|
|
|
− π 2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= R 4 |
3 |
|
|
1 |
2 |
|
= |
3 |
|
|
|
||||||
|
|
|
ϕ + s in 2 ϕ + |
|
s in 4 ϕ |
|
|
|
|
|
|
π R 4 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
8 |
|
− |
π |
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72
Лекция 51. Применение двойных интегралов для вычисления площади поверхности и решения задач механики
51.1. Вычисление площади поверхности с помощью двойного интеграла. Мы умеем вычислять площади поверхности цилиндра и конуса, переходя к их развёрткам на плоскость (рис. 51.1 и 51.2).
r
h |
S = 2π r h |
|
2π r
|
Рис. 51.1 |
|
|
|
Развёртка конуса с радиусом основания |
r и |
образующей |
l – это |
|
сектор круга радиуса l и |
длиной дуги |
2πr . |
Если всей |
длине |
окружности 2πl соответствует площадь πl2 , |
то сектору с длиной дуги |
|||
2πr соответствует площадь |
πrl . |
|
|
|
|
|
|
l |
|
|
S = πrl |
|
|
|
l |
|
|
|
|
r |
|
|
2πr |
|
|
|
|
|
|
r |
|
|
|
|
Рис.51. 2
Перейдём к более сложной ситуации. Рассмотрим в пространстве поверхность, заданную уравнением z = f ( x, y ) . Часть этой поверхности,
ограниченную линией Г , обозначим Q . Предполагаем при этом, что функция z = f ( x, y ) является непрерывной вместе со своими частными производными. Ставим задачу найти площадь S поверхности Q . Для её
решения можно использовать двойной интеграл. Но вначале нужно определить, что понимать под площадью поверхности в этом случае.
73
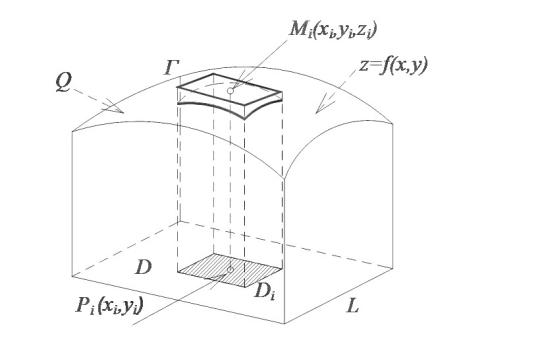
Проекцию пространственной линии Г на плоскость xOу обозначим
L . Проекцию поверхности Q на плоскость xOу обозначим D – |
это |
|
плоская область, ограниченная линией L . |
Разобьём область D на |
n |
частей D1, D2 , ..., Dn . В каждой подобласти |
Di выберем точку Pi ( xi , yi ) . |
|
Этой точке соответствует на поверхности |
Q точка M i ( xi , yi , zi ) (рис. |
|
51.3). |
|
|
Рис. 51.3
Проведём через точку Mi касательную плоскость |
αi к поверхности |
|||||||||||
Q . Её уравнение имеет вид |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
∂f |
|
∂f |
|
|
|||
z − zi |
= |
|
|
( x − xi ) + |
|
( y − yi ) , |
||||||
∂y |
||||||||||||
|
|
|
|
|
∂x i |
|
i |
|
||||
где коэффициенты |
∂ f |
|
и |
|
|
∂ f |
|
представляют собой значения частных |
||||
|
∂x |
i |
|
|
|
∂ y |
i |
|
|
|
|
|
производных функции |
z = f (x, y) |
в точке |
Mi (xi , yi , zi ). |
На касательной |
||||||||
плоскости выделим область Qi , которая проецируется на частичную подобласть Di в плоскости xOу (рис. 51.4). Площадь подобласти Qi обозначим qi . Если для всех частей Di плоской области найти соответствующие им области Qi на касательных плоскостях к исходной
|
n |
|
поверхности, то сумма их площадей |
I n = ∑ qi |
даст некоторое |
приближённое значение искомой площади. |
i =1 |
|
|
|
|
74 |
|
|
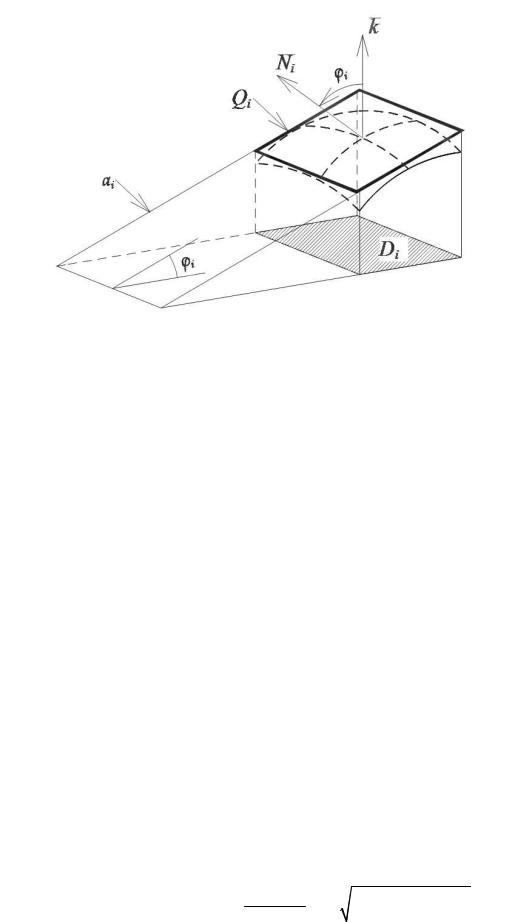
Рис. 51.4
Ясно, что чем «мельче» будет разбита область D на части, тем точнее сумма In будет соответствовать тому числу, которое следует считать
площадью поверхности Q . За точное значение S площади поверхности Q естественно принять предел сумм In при неограниченном увеличении числа подобластей Di . Как обычно, будем предполагать, что диаметр разбиения стремится к нулю при n → ∞ , т.е.
|
n |
qi . |
S = |
lim ∑ |
|
|
d n → 0 i =1 |
|
Итак, определение площади |
S мы |
дали. Чтобы её вычислить, |
необходимо связать величины площадей |
qi и Si плоских областей |
|
Qi и Di . Касательная плоскость αi |
образует с координатной плоскостью |
|
xOу двугранный угол, измеряющийся линейным углом, который мы
обозначим ϕ i |
(рис. 51.4). Поэтому |
qi |
= |
Si |
. |
|
| co s ϕi | |
|
|||||
|
|
|
|
|
|
|
Нормальный вектор к касательной плоскости αi |
имеет координаты |
|||||
UUUR |
, − ( f y′ ) ,1) , а нормаль |
|
|
|
|
|
N i = (− ( f x′ ) |
к |
плоскости |
xOу – вектор |
|||
i |
i |
|
|
|
|
|
k = {0 , 0 ,1} . Поскольку угол между плоскостями равен углу между
нормальными векторами к ним, для угла ϕ i |
получим соотношение |
||||||||||
|
|
|
UR UUR |
|
|
|
|
|
|||
|
|
(k, N i ) |
|
|
|
|
|
||||
| cos ϕ |= |
|
|
= 1/ |
( f ′) |
2 + ( f ′) 2 +1 |
||||||
|
|
UR |
|
UUR |
|
|
|||||
|
|
|
|
|
|||||||
i |
|
k |
|
N i |
|
|
|
x i |
y i |
||
|
|
|
|
|
|
|
|
|
|
||
Тем самым, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
75 |
|
|
|
|
|||||
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + ( f x′)i 2 + ( f y′)i 2 . |
|
|
|
|
|||||||||||||
|
∑ qi = ∑ Si |
|
|
|
|
||||||||||||||||
|
i =1 |
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Заметим, что это интегральная сумма для функции |
|
1 + z′ |
2 |
+ |
z′ 2 |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
поэтому формула пл ощади |
S всей поверхности |
Q |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
∂z |
2 |
|
|
∂z |
2 |
|
|
|
|
|
|||
|
l im |
|
|
|
∫∫ |
|
|
|
|
|
|
|
|
|
|||||||
S = |
∑ |
q |
i |
= |
|
|
∂x |
|
+ |
|
∂y |
|
|
|
|
|
|
||||
d n → 0 i =1 |
|
|
1 + |
|
|
|
|
d xd y . |
|
|
|||||||||||
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдём площад ь поверхности полусферы радиуса R (рис. 51.5). В декартовых коорди натах верхняя полусфера задается уравнением
z = 
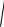 R2 −x2 − y2 .
R2 −x2 − y2 .
Рис. 51.5
Найдём подынтеграль ное выражение
|
|
|
|
|
|
∂z |
=− |
|
|
x |
|
, |
|
∂z |
=− |
|
|
y |
||||
|
|
|
|
|
|
∂x |
|
|
|
|
∂y |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
R2 |
−x2 −y2 |
|
|
R2 −x2 −y2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1+ ∂z 2 |
+ ∂z 2 = |
|
|
|
R |
|
. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
∂x |
∂y |
|
|
R2 − x2 − y2 |
||||||||
Область |
D |
представляет собой круг |
|
радиуса |
R в плоскости xOу. |
|||||||||||||||||
Поэтому, переходя к полярным координатам, получаем |
||||||||||||||||||||||
2π |
R |
R |
|
|
|
|
|
2π |
R |
|
|
|
|
|
1 |
|
|
|
|
2π |
||
S = ∫ dϕ∫ |
|
|
|
rdr |
=− ∫ dϕ∫ |
R2 (R2 −r2 )_ 2 d(R2 |
−r2 ) = ∫ R2dϕ=2πR2 . |
|||||||||||||||
|
|
|
|
|||||||||||||||||||
2 |
2 |
|||||||||||||||||||||
0 |
0 |
|
R −r |
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
76 |
|
|
|
|
|
|
|
|
|
|

51.2. Масса, статические моменты, координаты центра тяжести и моменты инерции плоской фигуры. Если плоскую область рассматривать как материальную пластинку, толщиной которой можно пренебречь, то с помощью двойного интеграла можно находить для неё координаты центра тяжести и моменты инерции относительно некоторой оси или точки.
Напомним, что для системы n материальных точек (xi , yi ) , с массами mi (i = 1, 2, K, n) , расположенных на плоскости координаты центра тяжести вычисляют по формулам
n |
n |
n |
n |
xc = ∑mi xi |
∑mi , yc = ∑mi yi |
∑mi . |
|
i=1 |
i=1 |
i=1 |
i=1 |
Величины |
n |
n |
|
|
|
||
M y = ∑mi xi , |
M x = ∑mi yi |
||
|
i=1 |
i=1 |
|
называются статическими моментами системы точек относительно координатных осей Oy и Ox .
Моментом инерцииI1 материальной точки P с массой m
относительно какой-либо оси называется произведение массы m на квадрат расстояния r от точки P до этой оси I1 = mr2 . Если в качестве r
рассматривается расстояние от точки P до точки O , то момент инерции точки P с массой m относительно точки O определяется по той же формуле. Моментом инерции системы n материальных точек с
массами mi (i = 1, 2, K, n) относительно оси или точки O называется
сумма моментов инерции точек системы, т.е., моменты инерции относительно координатных осей Oy и Ox имеют вид
n |
n |
Iny = ∑mi xi2 |
и Inx = ∑mi yi2 , |
i=1 |
i=1 |
а момент инерции относительно |
начала координат равен их сумме |
Ino = Iny + Inx . |
|
Физические понятия, рассмотренные для системы масс, перенесём на плоские области. Определим их для пластинки, занимающей некоторую
область D в плоскости xOу. Рассмотрим |
произвольную |
точку |
P |
||
пластинки, окружив её малой областью Di площади Si . Пусть |
Mi – |
||||
количество массы, приходящейся на площадь |
Si . Тогда приближённым |
||||
значением плотности области D можно считать их отношение |
γ = |
|
Mi |
. |
|
|
|
||||
i |
|
i |
Si |
||
77 |
|
|
|
|
|
Поверхностной плотностью γ в точке P называется предел приближённого значения плотности, если Di стягивается в точку и
Si → 0
γ = lim |
Mi |
. |
|
||
Si →0 |
S |
|
|
i |
|
В каждой точке области D поверхностная плотность, вообще говоря, своя, отличная от плотности в других точках, то есть поверхностная плотность является функцией точки. Поскольку точка P на плоскости xOу задаётся двумя координатами, получаем функцию двух переменных
γ= γ(x, y) .
Разобьём область D на малые подобласти Di , в каждой из которых выберем произвольную точку Pi (xi , yi ) с плотностью γ(xi , yi ) в
ней. Будем считать плотность подобласти Di |
постоянной и равной |
|
γ(xi , yi ) . Тогда масса Di |
равна M i ≈ γ(xi , yi ) |
Si , а приближённое |
значение массы M всей пластинки |
|
|
n |
n |
|
∑ |
M i ≈ ∑ γ(xi , yi ) Si . |
|
i=1 |
i=1 |
|
Точное значение массы рассматриваемой плоской пластинки D получим, устремив к нулю размеры частей Di , на которые она раздроблена
|
n |
Si = ∫∫ γ( x, y)dxdy . |
M = lim ∑ γ( xi , yi ) |
||
|
dn→0 i=1 |
D |
Если далее считать, |
что вся масса Mi |
подобласти Di сосредоточена в |
точке Pi (xi , yi ) , то |
можно рассматривать фигуру D как систему |
|
материальных точек. Это даёт приближённое значение статических моментов D относительно координатных осей Oy и Ox
n |
n |
|
n |
γ(xi, yi) Si . |
My ≈∑xi |
Mi ≈∑xi |
γ(xi, yi) Si, |
Mx ≈∑yi |
|
i=1 |
i=1 |
|
i=1 |
|
При диаметре разбиения, стремящемся к нулю, интегральные суммы перейдут в пределе в двойные интегралы, которые называются
статическими моментами плоской фигуры D относительно осей Oy и
Ox
78
M y = ∫∫ x γ( x, y )dxdy и M x = ∫∫ y γ( x, y )dxdy .
D D
Формулы, позволяющие вычислять координаты центра тяжести плоской фигуры, имеют тот же вид, что и для системы материальных
точек xc = |
M y |
, |
yc = |
M x |
, только статические моменты и масса |
|
M |
|
|
M |
|
вычисляются уже не через суммы, а с помощью двойных интегралов.
Для однородной пластинки D , имеющей постоянную во всех точках поверхностную плотность γ(x, y) ≡ γ, масса выражается через её площадь M = γS , а при вычислении статических моментов постоянный множитель γ можно вынести за знак двойных интегралов. Поэтому формулы для координат центра тяжести в этом случае приобретают вид
xc = |
1 |
∫∫ |
x d x d y , yc = |
1 |
∫∫ |
y d x d y . |
S |
S |
|||||
|
|
D |
|
|
D |
|
Рассуждая аналогичным образом, моментом инерции плоской фигуры D относительно некоторой оси или точки назовём двойной интеграл по этой области от функции, равной квадрату расстояния от точки фигуры до этой оси или точки. В частности, моменты инерции относительно координатных осей приобретут вид
I x = ∫∫ y2 γ(x, y)dxdy, |
I y = ∫∫ x2 γ(x, y)dxdy . |
D |
D |
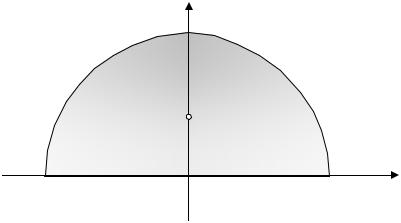
Определим координаты центра |
тяжести однородного полукруга |
радиуса R (см. рис. 51.6) |
|
y |
|
С(0,?)
|
Рис. 58.7 |
x |
− R |
O |
R |
|
Рис. 51.6 |
|
79

Перейдём в двойном интеграле к полярным координатам и вычислим
его
|
|
|
|
πR 2 |
∫∫ |
|
πR |
2 ∫∫ |
|
|
||
|
|
yc = |
2 |
|
ydxdy = |
2 |
|
|
|
r sin ϕ rdrd ϕ = |
||
|
|
|
D |
|
|
|
D |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
π |
R |
|
|
2 |
|
|
π |
R 3 |
s in ϕ d ϕ = 4 R . |
= |
|
∫ d ϕ ∫ r 2 s in ϕ d r = |
|
∫ |
||||||||
π R |
2 |
π R |
2 |
3 |
||||||||
|
0 |
0 |
|
|
0 |
3π |
||||||
Итак, центр тяжести полукруга имеет координаты (0, 43πR) .
Вычислим далее момент инерции круга радиуса R относительно его центра. Для этого начало координат расположим в центре круга. Считаем плотность постоянной γ =1. Тогда
I o = ∫∫ ( x 2 + y 2 )d xd y .
D
После перехода к полярным координатам получим
Io = ∫∫(r |
2 |
cos |
2 |
ϕ+ r |
2 |
sin |
2 |
2π |
R |
3 |
2π |
R4 |
πR4 . |
|
|
|
|
ϕ)rdrdϕ = ∫ d ϕ∫ r |
dr = ∫ |
4 d ϕ = |
2 |
||||||
D |
|
|
|
|
|
|
|
0 |
0 |
|
0 |
|
|
80
