Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

9395

.pdf

Скачиваний:

Добавлен:

25.11.2023

Размер:

2.62 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2115 16 17 18 19 20 21 > Следующая >>>

является обобщенным гармоническим рядом с показателем k =2, и

потому он сходится. Следовательно, рассматриваемый ряд сходится

абсолютно.

Принципиальную разницу между абсолютно сходящимися и условно сходящимися рядами дает следующая теорема.

Теорема. При любой перестановке членов абсолютно сходящегося

ряда (при этом можно переставлять как конечное, так и бесконечное число членов) получается сходящийся ряд, сумма которого равна сумме членов исходного ряда. При перестановке бесконечного числа членов условно сходящегося ряда можно получить условно сходящийся ряд, имеющий

любую наперед заданную сумму, и даже расходящийся ряд.

Последний факт можно увидеть на следующем примере. Пусть

∞	1		1		1		1		1		1		1		1+	1		1		1		1		1		1		1		1
S= ∑(−1)n+1		=1−		+		−		+		−		+		−			−		+		−		+		−		+		−		+...

n =1	n 2 3 4							5 6 7						8 9 10 11 12 13 14 15 16

Переставим члены этого ряда так, чтобы после одного положительного члена стояли два отрицательных. Будем иметь:

1 1

1 1 1

1 1 1 1 1

1−

−

+...=

−

+...=

3 6

8 5 10 12

7 14

2 4 6 8 10 12 14 16

1 1

1 1 1

1−

−

+....

2 3

5 6 7

Таким образом, путем перестановки бесконечного числа членов данного ряда получается ряд, сумма которого в 2 раза меньше суммы исходного ряда.

58.3. Функциональные ряды. Основные определения. Пусть имеется бесконечная последовательность функций

f1 (x), f2 (x),..., fn (x),...,

определенных в некоторой общей области

D . Если в данной записи все

запятые заменить знаками +, то полученная запись:

( x ) + f

( x ) + ... +

∞

( x )

(58.5)

( x ) + ... = ∑

n =1

будет называться функциональным рядом, определенным в области D .

Пусть, например, имеются три последовательности функций:

sin x		sin 2x		sin nx		x1		x2		x3		xn
	,		,...,		,...,		,		,		,...,		,....
12						13		23		33		n3
	22			n2

e x , e 2 x , e3 x ,..., e nx ,...

141

Им будут соответствовать функциональные ряды

( а) : ∑ sin n x	,	( в ) : ∑ x	n
			3
∞		∞

		n = 1 n
n =1 n 2

которые определены на всей числовой оси. Пусть имеется функциональный ряд (58.5),

D. Если взять произвольное число x0 из области

xв (5), то получится числовой ряд:

∞

, (с): ∑ enx ,

n =1

определенный в области D и подставить вместо

∞

f1 ( x0 ) + f 2 ( x0 ) + ... + f n ( x0 ) + ... = ∑ f n ( x0 ) .

(58.6)

n =1

Если ряд (58.6) сходится, то

называется точкой

сходимости

функционального ряда (58.5), в противном случае x0

называется точкой

расходимости. Совокупность всех точек сходимости

образует область

сходимости D0

функционального ряда (58.5).

Найдем

области

сходимости

приведенных

выше

функциональных рядов.

Рассмотрим ряд

(a).

Для

произвольного числа

x0 сравним ряд

∞

sin nx 0

∞

∑

и сходящийся ряд ∑

Т.к.

sin nx0

то по признаку

n 2

n =1

n = 1 n 2

sin nx0

∞ sin n x0

∞

сравнения

ряд

∑

сходится, и потому ряд

∑

сходится

n 2

n=1

n = 1

абсолютно при любом

x0 . Таким образом,

область сходимости ряда (а)

совпадает со всей числовой прямой.

Рассмотрим

ряд

(b).

Для

произвольного числа

рассмотрим

∞

x 0n

≤ 1 выполняется неравенство

числовой ряд ∑

. При

≤

n = 1

, и, следовательно, по признаку сравнения данный ряд абсолютно

сходится. Если же	x0		> 1, то
				( x0 ("			( x0 (
		+					( x0 (			x0
	∞	'								x0
	∞	'			*	∞				( ( - 1
lim				)	*	lim	+	)		( ( - 1
"&						"&	√		*
"&						"&			*

и, следовательно, по радикальному признаку Коши данный ряд абсолютно расходится. Последнее неравенство показывает также, что при

отрицательных x0 , таких, что x0 > 1 общий член рассматриваемого ряда к

0 не стремится и поэтому он не может сходиться и условно. Таким образом, область сходимости ряда совпадает с отрезком [-1,+1].

142

∞	при любом числе x0 представляет сумму членов
Ряд ∑ e nx	при любом числе x0 представляет сумму членов
n =1

бесконечной геометрической прогрессии со знаменателем q = ex0 . Такой ряд сходится только, если q < 1 . Т.к. неравенство ex0 > 0 выполняется при любом x , а неравенство ex0 <1 выполняется только при x0 <0,

то область сходимости рассматриваемого ряда совпадает с бесконечным интервалом (-∞,0). Причем в точке x0 его сумма равна

e x0

1 − e x0 .

Приведенные примеры показывают, что область сходимости функциональных рядов может быть самой разнообразной.

∞

Пусть имеется функциональный ряд ∑ f n ( x) с областью

n =1

определения D и областью сходимости D 0 . Через S(x) обозначим функцию, определенную в области D 0 , значение которой в точке x0 равно

∞

сумме числового ряда ∑ f n ( x0 ) . Функция S(x) называется суммой

n =1

функционального ряда. При этом говорят, что ряд сходится к функции

S(x) в области D 0 . Записывается это так:

∞

∑ f n ( x ) = S ( x)

n =1

143

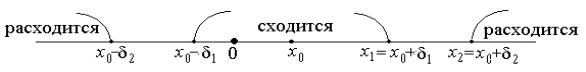
Лекция 59. Степенные ряды.

В предыдущей лекции наряду с числовыми рядами были введены функциональные ряды. Особое место среди функциональных рядов занимают степенные ряды. Их рассмотрению будет посвящена настоящая лекция.

59.1. Область сходимости степенного	ряда.	Теорема
Абеля.
Степенным рядом с центром в точке	x0 называется ряд
вида
∞
a0 + a1(x − x0 ) + a2 (x − x0 )2 + ...+ an (x − x0 )n + ... = ∑an (x − x0 )n ,		(59.1)
n=0

где a 1 , a 2 , a 3 ,..., a n ,... известные числа, называемые коэффициентами

степенного ряда.

Область сходимости произвольного степенного ряда имеет достаточно простую структуру. Для выяснения ее строения сформулируем сначала следующую теорему, доказательство которой похоже на доказательство признака Даламбера.

Теорема

Абеля

(Нильс Абель

(1802 – 1829) – норвежский

математик).

x = x1

Если при

степенной ряд (59.1) сходится, то он абсолютно

сходится при

x (x0 − δ1 , x0 + δ1 ) , где δ1 =

x2 − x0

Если при

x = x2

степенной ряд (1) расходится, то он расходится

при x

< x0 − δ2

и при x

> x0 + δ2 , где

δ2 =

x2 − x0

(рис 59.1).

Рис. 59.1

Из теоремы Абеля вытекает очень важное следствие о структуре области сходимости степенного ряда. А именно: область сходимости степенного ряда представляет собой открытый интервал, симметричный относительно центра степенного ряда x0 , к которому могут примыкать

один из концов или оба конца этого интервала. Иначе говоря, для всякого степенного ряда существует такое неотрицательное число R , называемое


радиусом сходимости степенного ряда,				что при значениях х из
интервала ( x0 − R, x0 + R) (т.е. когда		x − x0		< R ) ряд абсолютно сходится,
интервала ( x0 − R, x0 + R) (т.е. когда		x − x0		< R ) ряд абсолютно сходится,
а вне этого интервала (т.е. когда	x − x0		> R )	ряд расходится (рис. 59.2).
а вне этого интервала (т.е. когда	x − x0		> R )	ряд расходится (рис. 59.2).
144

Рис. 59.2

Как будет видно из нижеприводимых примеров, на концах данного интервала (т.е. при x = x0 − R и при x = x0 + R) м огут встречаться

различные ситуации, а именно: на обоих концах ряд может расходиться или на обоих концах ряд может сходиться, или на одном сходиться, а на другом расходиться. Причем и характер сходимости на концах интервала (условно или абсолютно) может быть различным.

Отметим, что могут встретиться два частных случая, когда

R = 0

когда R = +∞ .

Есл и R = 0 ,

то это означает,

что область сходимости

степенного ряда сост оит из единственной точки x = x0 , а если R = +∞ ,

то

это означает, что степенной ряд сходится при всех значениях x .

Признак Даламбера и радикальный признак

Коши

сходимости

знак оположительных

рядов

даю т

два

способа

нахождения радиус а сходимости степенного ряда (59.1).

Способ Даламбера. Если существует

n→∞

, то он равен радиусу

lim

n+1

сходимости степенного ряда, т.е.

R = lim

→∞ | a

n +1

Способ Коши.

lim n

Если существует

и он нее равен 0,

то

n →∞

R = 1 / lim

n → ∞

∞ 5n (x +1)n

Пример. Найти область сходимости D

ряда

∑

n=1

Центр данного

степенного

ряда

равен

x =−1,

. Для

коэффициентов степенного ряда имеем:

= n

¾¾®n→∞ 5 .

n n

Таким образом, радиус сходимости

R =1/ 5.

Значит,

ряд

сходится

абсолютно в интервал е (-6/5,-4/5).

145

Исследуем сходимость

ряда

на

концах данного

интервала. Пусть

x = −6 / 5 . Получаем числовой ряд:

∞

( x + 1)

∞

( − 1 / 5)

∞

( − 1)

∑

= ∑

n =1

который является знакочередующимся вариантом гармонического ряда и который, как ранее было показано, сходится условно.

Пусть x = −4/ 5. Получаем числовой ряд

∞

+ 1)

n ∞

(1/ 5)

n ∞

∑

= ∑

=∑

n=1

который является расходящимся гармоническим рядом. Таким образом, область D 0 = [− 6 / 5,−4 / 5 ).

Пример. Найти область сходимости ряда

∞

1 + x +

+ ... +

+ ...

= ∑

n =1

Находим радиус сходимости методом Даламбера:

R = lim

a n

= lim

( n + 1)!

= lim ( n + 1) = +∞ .

n →∞

a n +1

n →∞

Следовательно, данный ряд сходится при любом значении x .

∞

Пример. Найти область

сходимости

ряда

∑ n! x n . Проводя

n =1

рассуждения предыдущего примера, придем к выводу о том, что R = 0 и,

значит, данный ряд сходится лишь при x = 0 .

Пусть имеется степенной ряд (59.1) с областью сходимостиD0 . Через

f ( x) обозначим функцию, к которой

этот ряд сходится в области D0 . Из

общей теории функциональных рядов вытекают следующие факты:

1)Функция f ( x) непрерывна в любой замкнутой области, целиком лежащей в области D0 .

2)Если пределы интегрирования α,β лежат в областиD0 , то определенный интеграл от функции f (x) на участке [ α,β ] может быть

вычислен по формуле:

β β ∞

∫ f ( x)dx = ∫ ∑

αα n=0

∞ β

an ( x − x0 )n dx = ∑ ∫ an ( x − x0 )n dx .

n=0 α

146

Иначе говоря, интеграл от суммы ряда равен сумме ряда интегралов от его членов.

3) Во всех внутренних точках области D0 функция f ( x) дифференцируема, и ее производная может быть найдена по формуле

′	d	∞		n
f (x) =		∑ an ( x − x0 )
f (x) =		∑ an ( x − x0 )
	dx n =		0

∞

= ∑

n =0

d (an (x − x0 )n )= ∑∞ nan ( x − x0 )n −1 .
dx	n =0

Иначе говоря, производная от суммы ряда равна сумме ряда от производных его членов.

59.2. Ряды Тейлора – Маклорена. Все рассуждения о рядах,

изложенные в предыдущих разделах, были подготовительными к нижеприводимым утверждениям о том, что очень многие функции (практически все элементарные функции) могут быть представлены в виде степенных рядов. А т.к. в вычислении произвольного члена степенного ряда участвуют всего четыре арифметические операции, то это означает, что значения этих функций приближенно могут быть вычислены с использованием только этих операций.

Пусть функция f (x) определена в некоторой окрестности точки x0 , и в окрестности этой точки она имеет производные любого порядка.

Обозначив через f (n) (x0 ) составим ряд

f (x0 ) + f '(x0 )(x − x0 ) + 1!

значение n-ой производной функции в точке x0 ,

f ''(x	)			f	(n) x(	)
0	(x	− x )2	+ ... +		0	(x − x )n + ...
	(x	− x )2	+ ... +			(x − x )n + ...
2!		0			n!	0
2!					n!

∞

f (n) (x )

(59.2)

= f (x0 ) + ∑

(x − x0 )n

n=1

Этот степенной ряд называется рядом Тейлора функции

f ( x) в

окрестности точки x 0 .

Если x0 = 0 , то ряд (59.2) принимает вид

~ 0

′0

′′0

∞

" 0

и называется рядом Маклорена функции f (x).

Составим ряды Маклорена для функций

e x

, sinx ,

ln(1 + x) .

Для функции y = e x

значения самой функции и всех ее производных

в точке 0 равны 1.

Поэтому ряд Маклорена для нее имеет вид :

147

e x : 1 +

∞

+ ... +

+ .. = 1 + ∑

(59.3)

n=1 n!

Для функции

y = sinx

имеем:

при x0 = 0

сама функция и все ее

производные с четными номерами

равны 0; производные с номерами

1,5,9,… равны 1; производные с номерами 3,7,11,…

равны (–1). Таким

образом, ряд Маклорена для функции y = sinx имеет вид:

sin x:

(−1)n +1 x2 n −1

−

... +

(2n−1)!

+ ..

(59.4)

или кратко

∞

n +1

x2 n −1

sin x: ∑

(−1)

n=1

(2n−1)!

Составим таблицу производных для функции

f ( x ) = ln (1 + x ) .

f ( n ) ( x )

f (n) (0)

ln(1 + x)

(1 + x)-1

(-1) (1 + x)-2

(-1)

(-1)(-2) (1 + x)-3

(-1)(-2)= (-1)2 2!

(-1)(-2)(-3) (1 + x)-4

(-1)(-2)(-3)= (-1)3 3!

(-1)(-2)(-3)...(-n+1) (1 + x)-n

(-1)(-2)(-3)...(-n)=(-1)n-1 (n-1)!

Таким образом, ряд Маклорена для функции f ( x ) = ln (1 + x ) будет иметь вид:

ln (1 + x ):

( − 1) x 2

( − 1) 2 2 ! x 3

... +

( − 1) n − 1( n −1) ! x n

+ ...

или

2 !

x n +1

ln(1 + x) : x −

x 2

x 3

−

x 4

+ ... + (−1) n

+ ...

(59.5)

n + 1

Биномиальным рядом называется ряд Маклорена для функции f (x) = (1+ x)α

148

Нетрудно видеть,

что

f (n) (0) = α(α − 1)(α − 2)...(α − n + 1)

потому

биномиальный ряд выглядит следующим образом:

(1+x)α : 1 +

αx

α(α−1)x2

+ ... +

α(α−1)(α−2)...(α−n+1)xn

+ ...

(59.6)

Если α есть целое положительное число m, то производные, выше

m-го порядка, равны 0 и соотношение (5) превращается в равенство

(1+x)m = 1+

m(m−1)x

m(m−1)...(m− n +1)x

+ ... +

+ ...+xm = ∑Cmk xk

(59.7)

k=1

именуемое биномом Ньютона. Коэффициент

перед x k

обозначается C km и называется Он вычисляется по формуле

C km =

биномиальным коэффициентом.

	m!	.
	k ! ( m − k )!	.
	k ! ( m − k )!

Ряды Тейлора и Маклорена являются степенными рядами, каждый из которых имеют свою область сходимости. Естественно


возникает вопрос:		если ряд Тейлора составлен для функции f (x),
то каким числам		сходится такой ряд в точках из области
сходимости?	Для ответа на этот вопрос следует привлечь к
рассмотрению	следующий факт: для функции определенной в

окрестности точки x0 и имеющей в ней производные до (n+1)-го

порядка включительно, справедливо равенство, именуемое формулой Тейлора:

	f '(x )		f ''(x	)		f	(n) x(	)
f (x ) = f (x ) +	0	(x − x ) +	0	(x − x )2	+...+		0	(x − x )n + R (x ) ,		(59.8)
f (x ) = f (x ) +		(x − x ) +		(x − x )2	+...+			(x − x )n + R (x ) ,		(59.8)
0	1!	0	2!	0			n!	0	n
	1!		2!				n!

в котором величина Rn ( x) называется остаточным членом.

Сравнивая ряд Тейлора с формулой Тейлора, получаем следующий вывод. Если для некоторого значения x из области

сходимости ряда Тейлора остаточный член Rn ( x) в формуле (59.8)

стремится к 0 при n → ∞ , то ряд	Тейлора для функции			f (x)
сходится к значению этой функции в точке x .
Но как выяснить, верно ли, что	R	( x) → 0	при n → ∞ ? Для
	n
ответа на этот вопрос можно пользоваться			различными
формулами определения величины	R n ( x ) . По		одной из	таких

формул величина остаточного члена может быть записана в форме Лагранжа,

R		( x ) =	f ( n +1)	(c)	( x − x		)n +1	,	(59.9)
R	n	( x ) =	(n +	1)!	( x − x	0	)n +1	,	(59.9)
	n					0

				149

где f (n +1) (c) есть значение (n+1)-ой производной в некоторой точке с, находящейся на интервале ( x0 , x) .

Одно из достаточных условий сходимости ряда Тейлора для функции f (x) к значению этой функции в точке x приводится в

следующей теореме.

Теорема. Пусть модули всех производных функции f (x) в некоторой окрестности точки x0 ограничены одним и тем же числом С. Тогда для любой точки x из этой окрестности ряд Тейлора для функции f (x) сходится к значению этой функции в точке x.

Как правило, ряд Тейлора, составленный для функции f (x) ,

внутри области сходимости сходится к ее значениям в соответствующих точках. (Выделенные слова «как правило», подчеркивают тот факт, что следующее за ними предложение нельзя сформулировать в виде теоремы, ибо можно построить примеры, когда ряд Тейлора в области сходимости будет сходиться к значениям, отличным от значений функций, для которых он составлен.)

В частности, этот факт справедлив для функций, фигурирующих в соотношениях (59.3)-(59.5). Следовательно, в этих соотношениях в областях сходимости справа стоящих степенных рядов (и только в них) знак двоеточия может быть заменен на знак равенства.

Ранее было показано, что ряд в соотношении (59.3) сходится на всей числовой прямой и потому знак двоеточия может быть

заменен на знак равенства при любых значениях

x. В частности,

подставив x=1, получаем

∞

e = 1 +

+ ... +

+ .. = 1 +

∑

(59.10)

2 !

n =1 n !

В соотношении (59.3) знак двоеточия может быть также заменен на знак равенства при любых значениях x.

Ряд в правой части соотношения (59.5) сходится только в области (-1,1] и только в этой области знак двоеточия может быть заменен на знак равенства. В частности, если x =1, то получается равенство

ln 2 = 1 −	1	+	1	... +	(−1) n − 1	+ .. .	(59.11)
	2		3		n

150

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2115 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.20232.62 Mб09390.pdf
#
25.11.20232.62 Mб09391.pdf
#
25.11.20232.62 Mб09392.pdf
#
25.11.20232.62 Mб09393.pdf
#
25.11.20232.62 Mб09394.pdf
#
25.11.20232.62 Mб09395.pdf
#
25.11.20232.62 Mб09396.pdf
#
25.11.20232.62 Mб09397.pdf
#
25.11.20232.62 Mб09398.pdf
#
25.11.20232.62 Mб09399.pdf
#
21.11.202389.7 Кб094.pdf