
9051
.pdf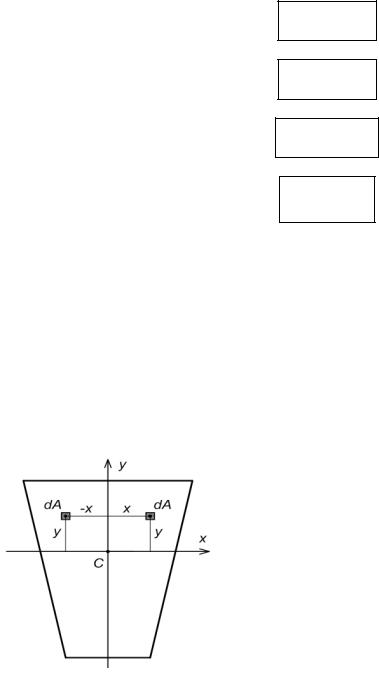
2.2. Моменты инерции сечений.
Для сечения, показанного на рис. 2.1, можно ввести следующие новые геометрические характеристики:
осевой момент инерции сечения относительно оси х:
Jx = ∫ y 2 dA ;
A
осевой момент инерции сечения относительно оси у:
Jy = ∫ x 2 dA ;
A
центробежный момент инерции сечения:
Jxy = ∫ xy dA ;
A
полярный момент инерции сечения:
Jp = ∫ ρ 2 dA .
Для моментов инерции можно указать следующие свойства:
моменты инерции имеют размерность мм4, см4 и т. д.;
осевые моменты инерции Jx, Jy и полярный момент инерции Jp всегда положительны и
не равны нулю;
центробежный момент инерции Jxy может быть положительным, отрицательным и равным нулю;
оси, относительно которых центробежный момент инерции равен нулю: Jxy = 0, в
дальнейшем будем называть главными осями инерции.
Рассмотрим сечение, у которого ось у, например, - ось сим-
метрии (рис.2.4).
Центробежный момент инерции двух площадок, расположен-
ных симметрично, равен:
dJxy = xydA – xydA = 0.
Интегрируя по площади сечения, имеем Jxy = 0.
Таким образом, центробежный момент инерции
Рис. 2.4
сечения относительно осей, из которых одна или обе являются осями симметрии, равен нулю.
Складывая осевые моменты инерции и учитывая, что ρ 2 = х2 + у2 (см. рис. 2.1), получим
Jx + Jy = ∫ y 2 dA + ∫ x 2 dA = ∫ (x 2 + y 2 ) dA = ∫ ρ 2 dA = Jp ,
A A A A
т.е. сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей рав-
на полярному моменту инерции относительно точки пересечения этих осей:
Jx + Jy = Jρ .
Осевой момент инерции сложного сечения относительно некоторой оси равен сумме осевых моментов инерции составляющих его частей относительно этой же оси.
Аналогично, центробежный момент инерции сечения относительно двух взаимно перпенди-
кулярных осей равен сумме центробежных моментов инерции составляющих его частей от-
носительно этих же осей.
Полярный момент инерции сложного сечения относительно некоторой точки равен сумме по-
лярных моментов инерции составляющих его частей относительно этой же точки.
Следует помнить, что нельзя суммировать моменты инерции, вычисленные относительно различных осей и точек.
2.3. Моменты инерции простейших сечений.
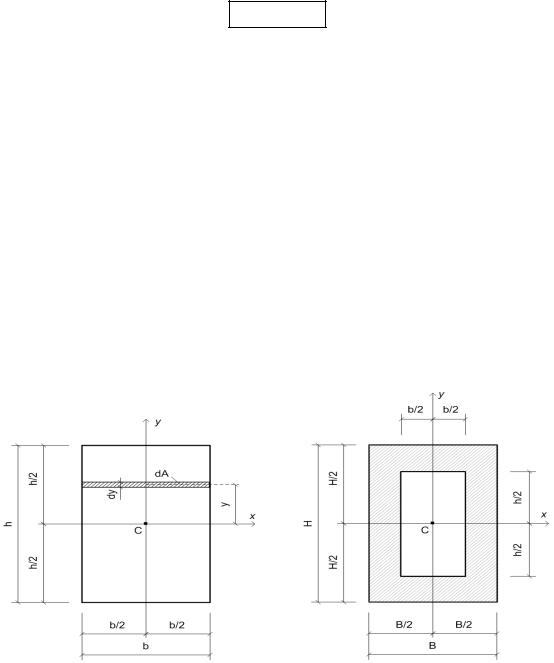
1). Осевые моменты инерции прямоугольного сечения шириной b и высотой h относительно осей симметрии прямоугольника х и у (рис. 2.5).
Рис. 2.5 |
Рис. 2.6 |
Выделим линиями, параллельными оси х, элементарную полоску высотой dy и шири-
ной b. Площадь этой полоски dA = b dy, а координата её центра тяжести – у. Пределы интег-
рирования: от y = - h/2 до y = + h/2. Вычислим осевой момент инерции прямоугольника от-
носительно оси симметрии х:
|
|
|
|
|
|
|
|
h / 2 |
b h |
3 |
|
||
|
|
|
Jx = ∫ y 2 dA = b ∫ y 2 dy = |
|
. |
||||||||
|
|
|
12 |
||||||||||
|
|
|
A |
|
|
|
|
−h / 2 |
|
||||
|
|
|
|
|
|
|
|
|
|
||||
Аналогично, J y |
= |
h b 3 |
. Оси х и у – |
оси симметрии фигуры, поэтому Jxy = 0. |
|||||||||
|
|||||||||||||
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
Для квадратного сечения h = b = a и |
J |
|
= J |
|
= |
a 4 |
. |
|
|
|
|||
x |
y |
|
|
|
|
||||||||
|
|
|
|
|
|
12 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
Для прямоугольного коробчатого сечения (рис. 2.6) моменты инерции равны разности моментов инерции большого прямоугольника и малого прямоугольника:
|
|
|
|
|
|
|
|
|
Jx |
= |
B H 3 − b h 3 |
; Jy |
= |
H B 3 − h b 3 |
|
|
; Jxy = 0 . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2). Равнобедренный треугольник |
3). Прямоугольный треугольник |
||||||||||||||||||||||||||||||||||
Jx |
= |
b h 3 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jx |
= |
|
b h 3 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
36 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
= |
h b 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jy |
= |
h b 3 |
|
|
|
|
|
|
|
|
|
|
||||
Jy |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
48 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jxy |
= ± |
b 2 h 2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Jxy = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
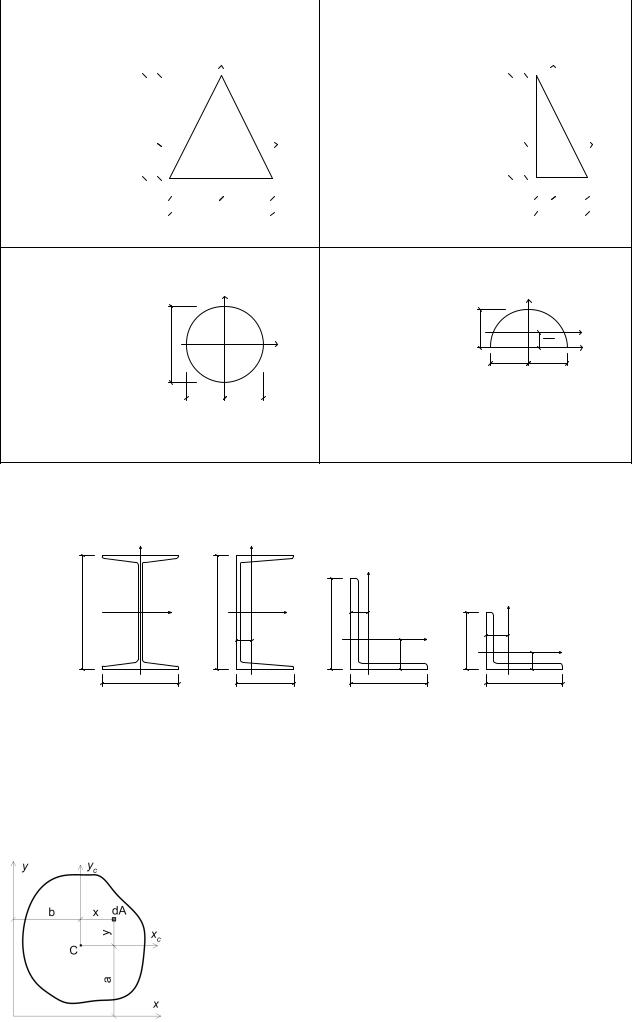
4). Круг |
|
|
5). Полукруг |
|
||
Jx |
= |
π d |
4 |
J x1 |
= π d 4 ; |
|
64 |
; |
|
128 |
4r |
||
|
|
|
|
= π d 4 |
3 π |
|
Jy |
= |
π d |
4 |
J y |
; |
|
|
; |
|
128 |
|
||
|
|
64 |
|
|
|
|
|
|
J |
x |
= π d 4 (1− |
64 |
) ; J |
xy |
= 0. |
|
|
|||||||
|
|
|
||||||
Jxy = 0 . |
|
|
128 |
9π 2 |
|
|||
|
|
|
|
|
||||
В строительстве широкое применение находит прокатная сталь. Сечения прокатных профилей показаны на рис. 2.7:
Рис. 2.7
Геометрические характеристики прокатных профилей определяют из таблиц на про-
катную сталь.
2.4. Преобразование моментов инерции при параллельном переносе осей.
Установим зависимость между моментами инерции одного и того же сечения относи-
тельно разных, но параллельных осей.
Предположим, что моменты инерции сечения относительно её цен-
тральных осей Jxc , Jyc , J xc yc известны (рис. 2.8).

Необходимо определить моменты инерции сечения относительно произвольных осей х и у, |
|
параллельных центральным осям хс и ус этого сечения. |
|
Используя обозначения рисунка 8, вычислим осевой момент |
инерции сечения относи- |
Рис. 2.8 |
тельно оси х. |
|
|
|
|
J x = ∫( y + а) 2 dA = ∫ y 2 dA + 2 a ∫ y dA + a 2 ∫dA = J xc + 2 a S xc + a 2 A . |
|||
|
A |
A |
A |
A |
Учитывая, что статические моменты фигур относительно центральных осей равны нулю:
Sxc = 0 , в результате получаем
Jx = Jxc + a 2 A .
Выполняя аналогичные вычисления для второго осевого момента инерции и центро-
бежного момента инерции, будем иметь следующие формулы преобразования моментов инер-
ции при параллельном переносе осей
Jx = Jxc + a 2 A . Jy = Jyc + b 2 A . Jxy = Jxc yc + a b A .
Из формул для осевых моментов инерции следует, что для всех параллельных осей наимень-
шее значение осевые моменты инерции имеют относительно центральных осей хс и ус.
Если заданное сечение можно разбить на простейшие фигуры, то полученные формулы вы-
числения моментов инерции при параллельном переносе осей можно записать в следующем виде
J x = ∑( J xi + a i2 A i ) ; J y = ∑( J yi + b i2 A i ) ; J xy = ∑( J xi yi + a i b i A i ) .
2.5. Преобразование моментов инерции при повороте осей.
Предположим, что моменты инерции сечения Jx, Jy, Jxy относительно заданной системы координат х, у известны. Повернём заданную систему координат вокруг начала координат на произвольный угол ά (рис. 2.9). Положительным будем считать угол поворота от положитель-
ного значения х к положительному значению у.
На рис. 2.9 показан положительный угол поворота для заданной системы координат.
Формулы, связывающие координаты центра тяжести элементарной площадки dA в новой (по-
вёрнутой) и старой системах координат, приведены на рис. 2.9.
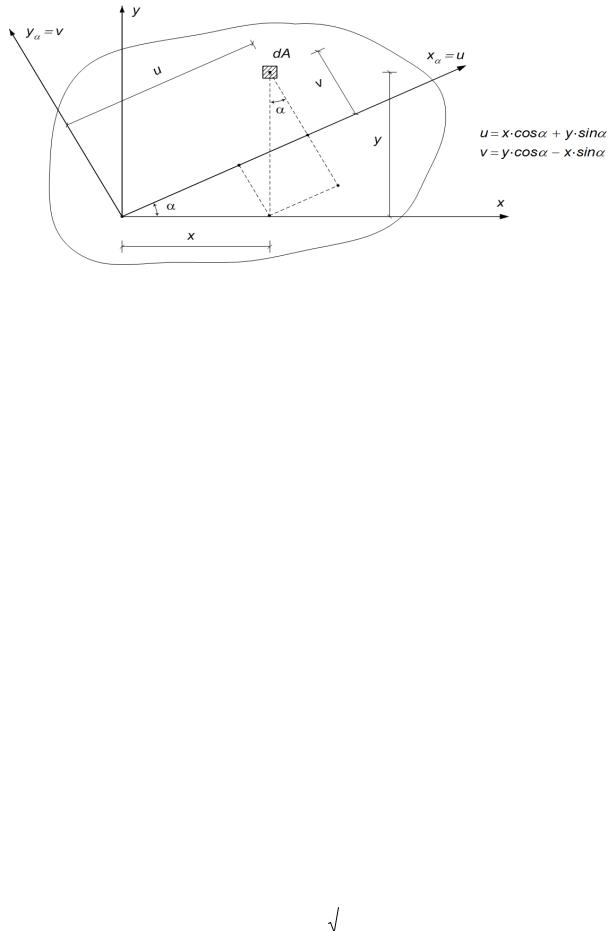
Рис. 2.9
2.6. Главные оси инерции. Главные моменты инерции.
Как было установлено ранее, Jx + Jy = Jp .
Если оси координат поворачивать в своей плоскости вокруг начала координат, то по-
лярный момент инерции останется неизменным, а осевые моменты инерции будут изменяться,
причём Jx + Jy = const.
Если сумма двух переменных величин остаётся постоянной, то одна из них уменьшает-
ся, а другая увеличивается. Следовательно, при каком-то положении осей один из осевых мо-
ментов инерции достигает максимального значения Jmax, а другой момент инерции - мини-
мального значения Jmin.
Оси, относительно которых моменты инерции имеют максимальное и минимальное зна-
чения, называются главными осями инерции, а моменты инерции – главными момен-
тами инерции.
В теории моментов инерции доказывается, что центробежный момент инерции равен
нулю: Jxy = 0 относительно главных осей инерции.
Ранее мы установили, что центробежный момент инерции равен нулю, если одна из
осей х или у – ось симметрии. Кроме того, ось симметрии – центральная ось.
Следовательно, оси симметрии фигуры являются главными центральными осями
инерции.
Величины главных моментов инерции можно определять по формуле
|
|
|
Jx + Jy |
|
1 |
|
|
|
|
J max |
= |
± |
|
( Jx − Jy ) 2 + 4 J 2xy . |
|||||
|
|
||||||||
|
|
2 |
2 |
|
|
|
|||
|
min |
|
|
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Ось, относительно которой момент инерции достигает максимального значения, называется осью максимум или первой главной осью инерции.
Ось, относительно которой момент инерции достигает минимального зна-
чения, называется осью минимум или второй главной осью инерции.
Поскольку сумма осевых моментов инерции должна оставаться постоян-
ной, то для проверки вычислений можно использовать равенство
Jx + Jy = Jmax + Jmin .
Углы наклона главных осей инерции относительного исходной оси х можно определять по следующим формулам
tg α max |
= |
|
Jxy |
; tg α min |
= |
|
Jxy |
. |
|
Jy |
− Jmax |
Jy |
− Jmin |
||||||
|
|
|
|
|
Из формул следует, что, если один из углов получится положительным, то другой бу-
дет обязательно отрицательным. Для проверки вычислений можно использовать условие, что сумма абсолютных значений углов должна быть равна девяносто градусов:
αmax + α min = 90o .
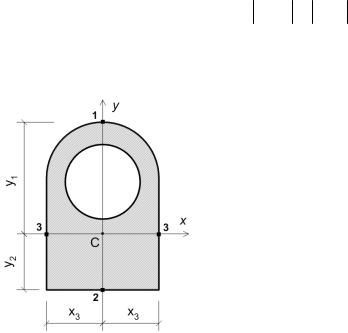
2.7.Моменты сопротивления сечений.
При решении задач изгиба и кручения используется геометрическая характеристика се-
чения, которая называется моментом сопротивления.
Осевым моментом сопротивления называют отношение главно-
го центрального момента инерции к расстоянию от главной цен-
тральной оси до самой удалённой точки на внешнем контуре се-
чения (рис.2.10):
Wx( 1) = |
|
|
J |
x |
|
|
; Wx( 2 ) = |
|
|
J |
x |
|
|
; Wy |
= |
|
|
Jy |
|
|
. |
|
|
y1 |
|
|
|
|
y2 |
|
|
|
|
x3 |
|
|
|||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Моменты сопротивления вычисляются в мм3, см3 и т. д.
Моменты сопротивления величины положительные и не равны нулю.
. Рис. 2.10 Моменты сопротивления сложных сечений не равны сумме моментов сопротивлений составных частей сечения, за исключением некоторых фигур.
Подсчитаем моменты сопротивления прямоугольного сечения (см. рис. 2.5).
|
|
|
b h 3 |
|
|
|
|
|
|
h b 3 |
|
|
|
|
||||
|
|
|
|
|
|
|
= |
b h 2 |
|
|
|
|
|
|
|
= |
h b 2 |
. |
W |
x |
= |
12 |
; W |
y |
= |
12 |
|||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
h |
|
6 |
|
|
|
b |
|
6 |
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
Момент сопротивления коробчатого сечения относительно оси х (рис. 2.6):

|
|
B H 3 − b h 3 |
|
B H 2 |
|
|
||
|
= |
12 |
= |
− |
||||
Wx |
|
|
|
|
1 |
|||
|
H |
|
6 |
|||||
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
Осевой момент сопротивления круглого сечения:
π d 4
Wx = Wy = |
64 |
= π d 3 |
||
|
||||
|
|
d |
|
32 |
|
2 |
|
|
|
b h 3 B H 3 .
.
При решении задач кручения круглых стержней используются полярный момент инерции и полярный момент сопротивления.
Полярный момент инерции круга: Jp = Jx |
+ Jy |
= π d 4 |
+ π d 4 |
= π d 4 . |
|||
|
|
|
64 |
64 |
32 |
||
|
|
|
π d 4 |
= π d 3 . |
|||
Полярный момент сопротивления круга: |
Wp |
= |
32 |
||||
|
|||||||
|
|
|
|
d |
|
16 |
|
|
|
|
2 |
|
|
|
|
2.8 Примеры решения задач на геометрию сечения
Задача 1. Для заданного поперечного сечения стального стержня, состоящего из следую-
щих элементов:
1.вертикального листа 400 х 12 мм;
2.прокатного двутавра №20;
3.прокатного швеллера №20;
4.неравнополочного уголка 100 х 65 х 10 мм,
необходимо определить:
-положение центра тяжести поперечного сечения (т. С);
-главные центральные оси поперечного сечения;
-главные центральные моменты инерции поперечного сечения;
-главные центральные радиусы инерции сечения.
Ре ш е н и е.
Геометрические характеристики элементов, составляющих заданное сечение:
№ |
|
Площадь в |
Моменты инерции сечения элементов в см4 |
||||||
эл- |
|
|
см2 |
|
|
|
|
|
|
Элементы |
|
|
Jx i |
|
Jy i |
Jx i y i |
|||
та |
|
|
Аi |
|
|
|
|
|
|
1 |
Вертикальный лист |
А1 |
= 48.0 |
Jx 1 |
= 6400 |
Jy 1 |
= 5.76 |
Jx 1 y 1 |
= 0 |
|
400х12 |
|
|
|
|
|
|
|
|
2 |
Двутавр №20 |
А2 |
= 26.8 |
Jx 2 |
= 115 |
Jy 2 |
= 1840 |
Jx 2 y 2 |
= 0 |
3 |
Швеллер №20 |
А3 |
= 23.4 |
Jx 3 |
= 1520 |
Jy 3 |
= 113 |
Jx 3 y 3 |
= 0 |
4 |
Уголок 100х65х10 |
А4 |
= 15.67 |
Jx 4 |
= 51.68 |
Jy 4 |
= 155.52 |
Jx 4 y 4 |
= 51.18 |
1). Общая площадь составного сечения
А = ∑ А i = 48.0 + 26.8 + 23.4 + 15.67 = 113.87 см2.
2). Статические моменты заданного сечения относительно осей х1 и у1 |
|
||||||||||||||
Sx 1 |
= ∑ Ai y i |
= 48 · 0 + 26.8 · 15 + 23.4 · (-10) + 15.67 · (-18.36) = - 119.7 см3, |
|||||||||||||
Sy 1 |
= ∑ Ai xi |
= 48 · 0 + 26.8 · 10.6 + 23.4 · 2.67 + 15.67 · (-3.97) = 284.35 см3. |
|||||||||||||
3). Координаты центра тяжести составного сечения |
|
|
|
|
|
|
|||||||||
|
|
xc = |
Sy |
1 |
= |
284.35 |
= 2.50 |
см, yc = |
Sx |
1 |
= |
−119.7 |
= −1.05 |
см. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
A |
|
113.87 |
A |
|
113.87 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
4). Координаты центров тяжести элементов сечения относительно осей х и у |
|||||||||||||||
точка С1: a1 |
= 1.05 см, |
|
|
|
|
|
b1 = - 2.5 см; |
|
|
|
|
|
|||
точка С2: а2 |
= 15 + 1.05 = 16.05 см, |
|
b2 = 10.6 – 2.5 = 8.1 см; |
|
|
||||||||||
точка С3: а3 |
= - (10.0 – 1.05) = - 8.95 см, |
b3 = 2.67 – 2.50 = 0.17 см; |
|
||||||||||||
точка С4: а4 |
= - (18.36 – 1.05) = - 17.31 см, |
b4 = - (3.97 + 2.5) = - 6.47 см. |
|
||||||||||||
5). Моменты инерции сечения относительно осей х и у
Jx = ∑( Jx i + Ai ai2 ) = [6400 + 48 · 1.052] + [115 + 26.8 ·16.052] +
+ [1520 + 23.4 · (-8.95)2] + [51.68 + 15.67 · (-17.31)2] = 21613.04 см4,
Jy |
= ∑( Jy i + Ai bi2 ) = [5.76 + 48 · (-2.5)2] + |
[1840 + 26.8 · 8.12] + |
|
|
|
||||||||||||||
|
|
+ [113 + 23.4 · 0.172] + [155.52 + 15.67 · (-6.47)2] = 4829.27 см4, |
|
|
|||||||||||||||
Jxy |
= ∑( Jx i y i + Ai ai bi |
) = [0 + 48 · 1.05 · (-2.5)] |
+ [0 + 26.8 ·16.05 · 8.1] |
+ |
|
||||||||||||||
|
|
+ [0 + 23.4 · (-8.95) · 0.17] + [51.18 + 15.67 · (-17.31) · (-6.47)] = 5128.68 см4. |
|||||||||||||||||
6). Главные центральные моменты инерции заданного сечения |
|
|
|||||||||||||||||
|
|
|
|
|
J max |
= J1,2 = |
Jx + Jy |
|
± |
1 |
[(Jx - Jy )2 + 4 J 2xy ] = |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
min |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
21613.04 + 4829.27 |
± |
1 |
|
[(21613.04 - 4829.27)2 + 4×5128.68 2 ] |
= 13221.16 ± 9834.99. |
|||||||||||||
|
|
|
|||||||||||||||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Jmax |
= J1 = 23056.15 см4, |
|
Jmin = J2 = 3386.17 |
|
см4. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверка: Jx + Jy = 21613.04 + 4829.27 = 26442.31 см4,
J1 + J2 = 23056.15 + 3386.17 = 26442.32 см4.
7). Углы наклона главных центральных осей инерции сечения |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
tgα max |
= |
|
|
Jxy |
|
|
= |
|
|
|
|
|
5128.68 |
|
= - 0.28138, |
|
α max |
= -15.72 |
o |
. |
|
|
||||||||||||||||
|
Jy |
|
|
|
|
|
4829.27 - 23056.15 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
- Jmax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
tgα min |
= |
|
|
Jxy |
|
|
|
= |
|
|
|
|
|
|
5128.68 |
|
|
= 3.5539325, |
|
αmax |
= |
74.28 |
o |
. |
|
|
||||||||||||
Jy |
|
|
|
|
|
4829.27 - 3386.17 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
- Jmin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Проверка: |
|
αmax |
|
+ |
|
α min |
|
= 15.72o + 74.28o = 90o. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
8). Главные центральные радиусы инерции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
imax |
= |
|
|
Jmax |
|
= |
|
23056.15 |
|
= 14.23 см, |
imin = |
Jmin |
|
|
= |
|
3386.17 |
|
= 5.45 см. |
||||||||||||||||||
|
|
|
A |
113.87 |
A |
113.87 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
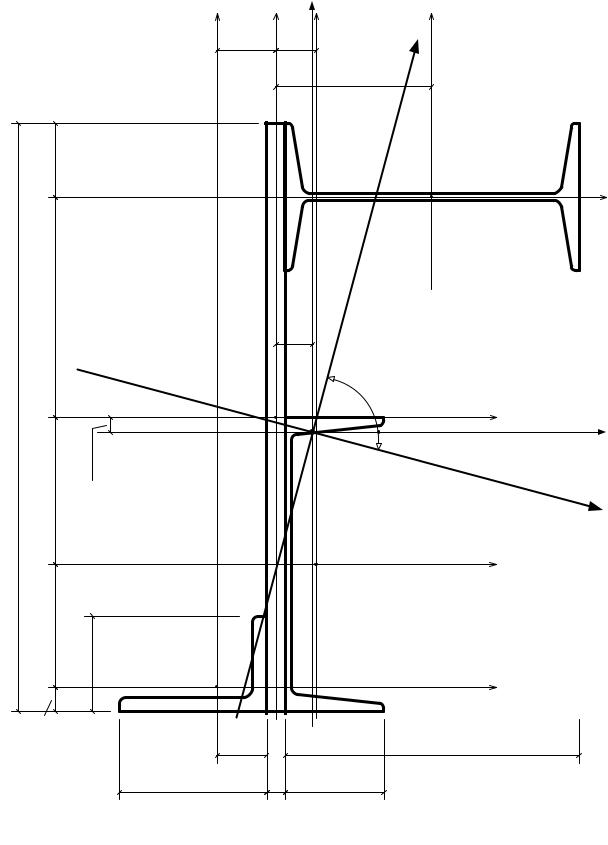
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
у4 |
|
у1 |
у3 |
|
|
|
|
у2 |
|
|
|
|
3.97 см |
|
2.67 см |
min (2) |
|
|
|
|
|
|||
|
|
|
|
10.60 см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х2 |
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
2.50 см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
.2 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
= |
7 |
|
|
|
|
|
|
|
|
|
|
|
IN |
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
c |
1 |
|
|
|
|
|
|
|
|
х1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
MAX = - |
15. |
72 |
O |
х |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max (1) |
|
|
|
|
|
|
|
|
|
|
|
|
х3 |
|
|
|
|
c3 |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
х4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
3.37 см |
|
|
|
|
|
|
20.00 см |
|
|||
10.00 см |
1.20 см |
7.60 см |
|
|
|
|
|
|
|
|||
|
|
|
Рис.2.11 |
|
|
|
|
|
|
|
|
|
