
9051
.pdfмента. Сосредоточенные моменты выражаются в единицах силы, умноженных на единицу длины (Н·м, кН·м и т.д.).
2). По характеру нагрузки делятся на статические, динамические и повторно-
переменные.
-К статическим относятся нагрузки, не меняющиеся со временем (например, нагрузки от собственного веса) или меняющиеся настолько медленно, что вызываемые ими ускорения и силы инерции элементов конструкции пренебрежимо малы (например, снеговая нагрузка).
-Динамические нагрузки в отличие от статических нагрузок меняют своё значение, по-
ложение или направление в короткие промежутки времени (движущиеся нагрузки, ударные,
сейсмические и др.), вызывая большие ускорения и силы инерции, которые необходимо учи-
тывать при расчёте.
- Повторно-переменные нагрузки многократно меняют со временем своё значение или значение и знак. Разрушение материала под действием таких нагрузок называется усталост-
ным, а способность противостоять ему – сопротивлением усталости.
3). По продолжительности нагрузки делят на постоянные и временные.
- К постоянным относятся нагрузки, действующие в течение всего времени существо-
вания конструкции или сооружения (например, вес конструкции, вес и давление грунта).
- Временные нагрузки действуют на протяжении отдельных периодов эксплуатации или возведения объекта. К ним относятся нагрузки от веса людей, материалов и оборудования;
давление жидкости, газов, сыпучих материалов; атмосферные нагрузки (снеговая, ветровая,
гололёдная); температурные, монтажные, сейсмические и прочие воздействия ограниченной продолжительности.
1.5 Понятие о внутренних силах.
Во втором параграфе была введена модель тела (модель материала), которая имеет сле-
дующие фундаментальные свойства: свойство сплошности, свойство однородности, свойство изотропности, свойства идеальной упругости. Теперь необходимо рассмотреть модель пове-
дения тела под действием внешних сил и других воздействий (например, температурных).
Внешние воздействия вызывают деформацию тела. В каждой точке тела возникает
внутренняя сила сопротивления (реакция) внешнему воздействию. Внутренние силы
можно рассматривать как реакции внутренних связей, обеспечивающих це-
лостность тела при его деформировании.
При изменении нагрузки будут меняться и внутренние силы, т. е. значение введённых внутренних сил зависит от внешних воздействий. При возрастании внешних сил увеличива-
ются и внутренние силы, но лишь до определённого предела, при превышении которого на-
ступает разрушение. Это предельное значение внутренних сил зависит от физико-
механических свойств материала данного тела.
Из введённого понятия внутренних сил следует, что внутренние силы определяются через внешние и что их величина ограничена свойствами материала тела. Таким образом, для расчёта на прочность необходимо иметь возможность определять внутренние силы по задан-
ным внешним силам.
Поскольку внутренние силы можно рассматривать как реакции внутренних связей тела,
то для их определения можно использовать законы теоретической механики и в частности ак-
сиому связей, которая гласит: равновесие тела сохраниться, если действие связей заменить их реакциями. Отсюда вытекает метод определения внутренних сил, который называется мето-
дом сечений. Рассмотрим суть этого метода.
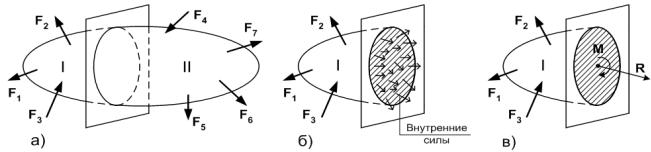
Пусть некоторое тело, находится в равновесии под действием заданных внешних сил
(рис. 1.4а). Напоминаем, что в число внешних сил F1,…, F7 входят как заданные активные си-
лы, так и реакции связей, закрепляющих тело в пространстве.
Рис. 1.4
Разрежем мысленно тело на две части некоторой произвольной плоскостью. Одну из частей (например, II) мысленно удаляем (отбрасываем) и рассматриваем оставленную часть I (рис. 1.4б). В каждой точке полученного сечения (разреза) необходимо приложить силы, кото-
рые для целого тела есть внутренние силы и которые являются силами взаимодействия между частями I и II тела. Закон распределения этих сил по сечению неизвестен, но, как любую сис-
тему сил, их можно заменить главным вектором R и главным моментом М (рис. 4в). Показан-
ные в сечении силы заменяют действие отброшенной части II на оставленную часть I и явля-
ются для части I внешними силами. Таким образом, применяя метод сечений, переводят си-
лы, являющиеся внутренними для тела в целом, во внешние для одной из его частей.
Внешние силы F1, F2, F3, действующие на рассматриваемую часть I, и силы в сечении
(рис. 1.4б,в) должны находиться в равновесии. Поэтому, составляя к отсечённой части тела
(рис. 1.4в) уравнения равновесия, можно выразить искомые внутренние силовые факторы R и
М через заданные внешние силы (нагрузку).
Мы рассмотрели равновесие части I тела. Принципиально совершенно безразлично, ка-
кую из частей тела (I или II) отбросить, так как из третьего закона Ньютона следует, что силы,
действующие от части II на часть I, равны по модулю и противоположны по направлению си-
лам действия части I на часть II. Практически удобно оставлять ту часть, к которой приложено меньше сил, так как уравнения для неё будут иметь более простой вид.
1.6. Внутренние силы в поперечном сечении бруса.
Рассмотрим определение внутренних сил в поперечном сечении бруса. Для этого сформулируем основные положения метода сечений:
1.разрезаем брус в интересующем месте плоскостью, перпендикулярной к оси бруса, на две части;
2.отбрасываем мысленно одну из образовавшихся частей (обычно ту, к которой прило-
жено больше сил), в результате чего нарушается равновесие оставшейся части;
3.заменяем действие отброшенной части на оставшуюся часть бруса внутренними сила-
ми;
4.составляем уравнения равновесия всех сил, приложенных к оставшейся части, из кото-
рых находим значения искомых внутренних сил через заданные внешние силы.
Систему координат для бруса выбираем следующим образом:
∙ось z – продольная ось бруса, проходящая через центры тяжести поперечных се-
чений его;
∙оси х и у – главные, центральные оси инерции поперечного сечения бруса, в ча-
стности, это оси симметрии.
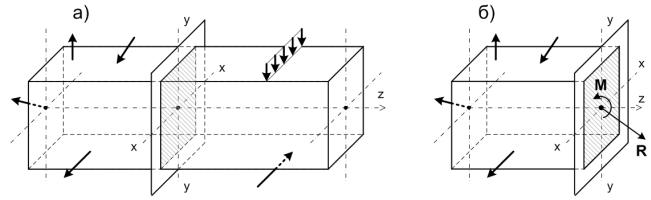
Пусть задан прямой брус, находящийся в равновесии под действием произвольной сис-
Рис. 1.5
темы внешних сил (рис. 1.5а). Рассечём его на две части некоторой произвольной плоскостью,
перпендикулярной к продольной оси z.
Одну из двух частей, например, правую отбрасываем, а в поперечном сечении оставшейся ле-
вой части прикладываем внутренние силы, которые заменяем статически эквивалентной сис-
темой сил – главным вектором R и главным моментом М, приведённым к центру тяжести се-
чения (рис. 1.5б).
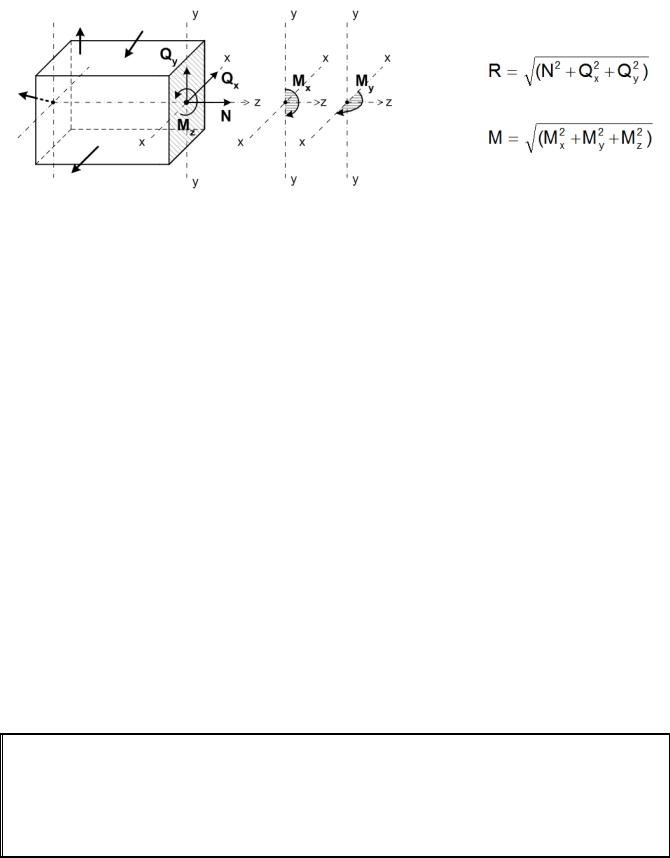
Каждый из этих двух векторов раскладываем на составляющие по осям координат (рис.1.6):
Qx, Qy, N - проекции главного вектора внутренних сил R на оси x, y, z.
Mx, My, Mz - проекции главного момента внутренних сил М на оси x, y, z.
Рис. 1.6
Полученные компоненты главного вектора и главного момента называются внутренними си-
ловыми факторами или усилиями.
Указанные шесть внутренних силовых факторов имеют следующие наименования:
N – продольная или нормальная сила,
Qx, Qy – поперечные силы в направлении соответствующих осей,
Mx, My – изгибающие моменты относительно соответствующих осей,
Mz - крутящий момент.
Для определения каждого внутреннего силового фактора надо составить соответст-
вующее уравнение равновесия для всех сил, действующих на оставленную часть бруса (рис.
1.6). Как известно, для пространственной системы сил таких уравнений может быть составле-
но шесть и в каждое из них войдёт лишь один внутренний силовой фактор, который и будет
определён из этого уравнения.
Σ x = 0: |
Qx + Σ Fix = 0, Qx = - Σ Fix . |
|
Σ y = 0: |
Qy + Σ Fiy = 0, Qy = - Σ Fiy . |
|
Σ z = 0: |
N + Σ Fiz = 0, N = - Σ Fiz . |
|
Σ mx = 0: |
Mx + Σ mx(Fi) = 0, |
.Mx = - Σ mx(Fi). |
Σ my = 0: |
My + Σ my(Fi) = 0, |
.My = - Σ my(Fi). |
Σ mz = 0: |
Mz + Σ mz(Fi) = 0, |
Mz = - Σ mz(Fi). |
На основании полученных уравнений можно сформулировать правила для определения
внутренних сил в поперечном сечении бруса.
Продольная сила N в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на продольную ось бруса z всех внешних сил, приложенных по одну сторону от рассматриваемого сечения.
Поперечные силы Qx и Qy в произвольном поперечном сечении бруса численно равны алгебраической сумме проекций на оси поперечного сечения бруса х и у всех внешних сил, приложенных по одну сторону от рассматриваемого сечения.
Изгибающие моменты Мx и Мy в произвольном поперечном сечении бруса численно равны алгебраической сумме моментов относительно осей поперечного сечения бруса х и у всех внешних сил, приложенных по одну сторону от рассматриваемого сечения.
Крутящий момент Мz в произвольном поперечном сечении бруса численно равен алгебраической сумме моментов относительно продольной оси бруса z всех внешних сил, приложенных по одну сторону от рассматриваемого сечения.
Правило знаков внутренних сил на плоскости y0z:
Усилие N > 0, если вызывает растяжение в поперечном сечении стержня (направлено «от сечения» и в левой и в правой его частях).
Усилие 

 > 0, если (совместно с внешней нагрузкой) стремится повернуть отсеченную часть стержня по часовой стрелке.
> 0, если (совместно с внешней нагрузкой) стремится повернуть отсеченную часть стержня по часовой стрелке.
Усилие 

 > 0, если вызывает растяжение в нижних волокнах стержня.
> 0, если вызывает растяжение в нижних волокнах стержня.
Усилие Мz > 0, если действует против часовой стрелки при взгляде на сечение со стороны внешней нормали.
1.7. Напряжения. Связь между напряжениями и внутренними силами в поперечном сечении бруса.
Внутренние силы, как уже указывалось, распределены по сечению тела (в частности,
бруса) сплошным образом, при этом в общем случае их значение и направление в отдельных точках сечения различны. Для суждения об интенсивности внутренних сил в определённой точке данного сечения вводится понятие о напряжении.
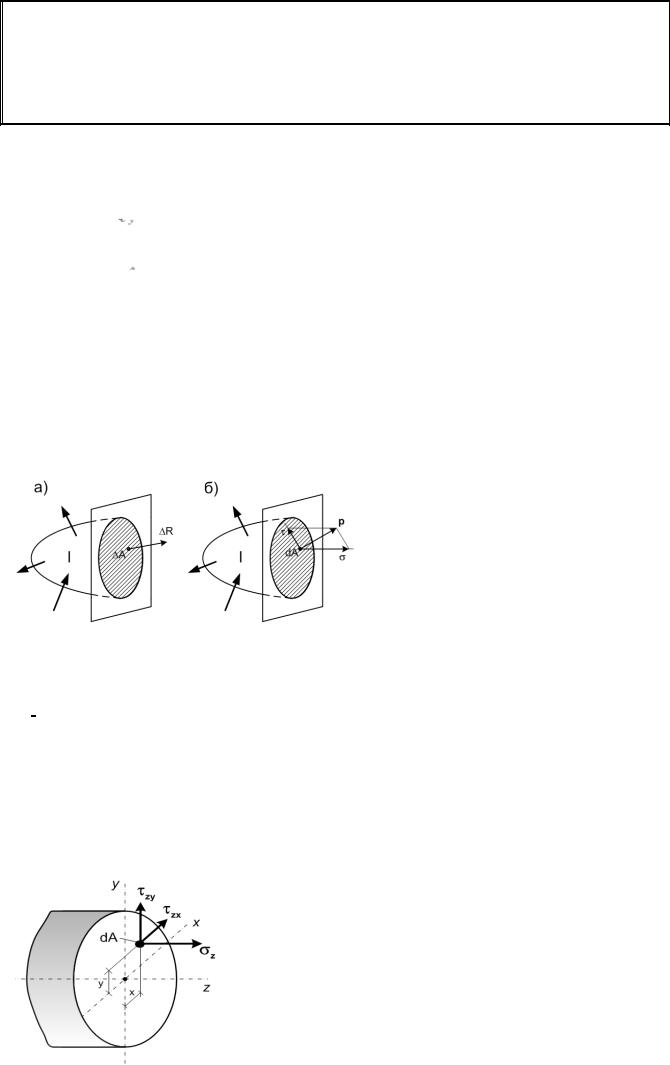
Выделим в окрестности интере-
сующей нас точки сечения малую пло-
щадку, площадью ∆А. Допустим, что на этой площадке возникает внутренняя сила
∆R (рис. 1.7а). Отношение этой внутрен-
Рис. 1.7 ней силы к площади выделенной площад-
ки называется средним напряжением рср в окрестности рассматриваемой точки по проведён-
ному сечению (по площадке ∆А):
рср = ∆R/∆А.
В пределе при стремлении ∆А к нулю получим истинное напряжение в данной точке рас-
сматриваемого сечения:
p = lim |
R = |
dR |
. |
|
|||
A→0 |
A dA |
||
В Международной системе единиц (СИ) в качестве единицы напряжения принят пас-
каль (Па). Паскаль – это напряжение, при котором на пло-
щадке в 1 м2 возникает внутренняя сила, равная 1Н. Но эта единица очень мала, поэтому используется кратная ей едини-
ца – мегапаскаль, 1 МПа = 106 Па.

Разложим вектор напряжения р на две составляющие: одну – направленную по норма-
ли к сечению, вторую – лежащую в плоскости сечения (рис.1.7б). Составляющую вектора на-
пряжения p, направленную по нормали к площадке её действия, называют нормальным на-
пряжением и обозначают σ (сигма), а составляющую, лежащую в плоскости сечения, - каса-
|
тельным напряжением и обозначают τ (тау). Между напряжениями р, σ и τ существует |
||||||||
|
|
|
|
p = |
|
|
. |
||
|
|
следующая зависимость: |
|
σ2 + τ2 |
|||||
.8 |
Установим теперь связь между напряжениями и внутренними силовыми факторами в попе- |
||||||||
|
|||||||||
|
речном сечении бруса (рис. 1.8). Разложим полное напряжение на три составляющие, направ- |
||||||||
|
ленные параллельно координатным осям. На рис. 1.8 показано это разложение применительно |
||||||||
|
к произвольной точке поперечного сечения бруса. |
|
|
|
|
||||
|
Для этих трёх составляющих принято следующее правило индексов: первый индекс |
||||||||
|
указывает, какой оси параллельна нормаль к площадке, а второй индекс показывает, вдоль ка- |
||||||||
|
кой оси действует данное напряжение. Обычно у нормального напряжения принято писать |
||||||||
|
лишь один индекс. |
|
|
|
|
|
|
|
|
|
Зависимость между полным напряжением и тремя его составляющими выражается оче- |
||||||||
|
видной формулой p = |
|
. |
|
|
|
|
|
|
|
σ2z + τ2zx + τ2zy |
|
|
|
|
|
|||
|
Умножая напряжения σz,, τzx , τzy |
на площадь dA площадки их действия, получим эле- |
|||||||
|
ментарные внутренние силы: |
|
|
|
|
|
|
|
|
|
|
dN = σz dA, |
dQx = τzx dA, |
dQy = τzy dA. |
|||||
|
Суммируя эти элементарные силы по всей площади сечения, получим выражения со- |
||||||||
|
ставляющих главного вектора внутренних сил в сечении: |
|
|
|
|||||
|
|
||||||||
|
N = ∫ σz dA , Qx = ∫ τzx dA , Qy = ∫ τzy dA . |
||||||||
|
|
A |
|
|
A |
|
|
A |
|
|
|
||||||||
|
Умножая каждую из элементарных сил на расстояние до соответствующей оси, полу- |
||||||||
|
чим элементарные моменты внутренних сил: |
|
|
|
|
||||
|
dMx = dN · y = (σz dA) · y; |
|
|
|
|
|
|
|
|
|
dMy = dN · x = (σz dA) · x; |
|
|
|
|
|
|
|
|
|
dMz = dQy · x - dQx · y = (τzy dA) · x - (τzx dA) · y. |
|
|
|
|
||||
|
Суммируя элементарные моменты по всей площади сечения, получим выражения для состав- |
||||||||
|
ляющих главного момента внутренних сил: |
|
|
|
|
||||
|
|
|
|
|
|||||
|
Mx = ∫ σz y dA , |
My = ∫ σz x dA , |
Mz |
= ∫ (τzy x dA − τzx y dA). |
|||||
|
A |
|
A |
|
|
|
A |
||
|
|
|
|
|
|
|
|
|
|
Таким образом, задача сопротивления материалов об определении напряжений, возни-
кающих в поперечных сечениях бруса при различных видах его нагружения, состоит в сле-
дующем: с помощью метода сечений определяем внутренние силовые факторы, а затем
из полученных формул находим напряжения.
1.8. Понятие о деформациях.
Под действием нагрузки тело деформируется, т.е. его формы и размеры изменяются.
Деформация состоит из двух частей: упругой, обратимой деформации, которая исчезает по-
сле удаления нагрузки, и неупругой, остаточной деформации, которая не исчезает после удаления нагрузки. Неупругая деформация, которая не сопровождается разрушением, называ-
ется пластической деформацией.
Деформации тела могут развиваться с течением времени при неизменной нагрузке. Та-
кие деформации называются деформациями ползучести.
Термин «деформация» употребляют в сопротивлении материалов в двояком смысле: в
первом - под деформацией подразумевают изменение формы и размеров тела, во втором – под деформацией рассматривают изменение длин и углов в окрестности точки тела. Рассмотрим та-
кие деформации.
|
|
|
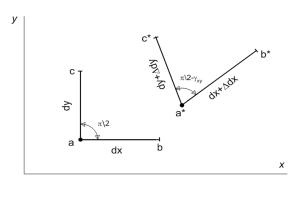
Мысленно через точку а тела проведём бесконеч- |
|||
|
|
|
но малые отрезки, параллельные осям координат |
|||
|
|
|
ab и ac. Длина этих отрезков равна dx, dy. На рис. |
|||
|
|
|
1.9 показаны эти отрезки в плоскости ху. При де- |
|||
|
|
|
формировании тела эти отрезки перемещаются |
|||
|
|
|
(положение |
a*, b*, c*), при этом длины отрезков |
||
|
|
|
и углы между ними изменяются. |
|||
Рис. 1.9 |
|
|
|
Изменение длин отрезков ∆x, ∆y, ∆z на- |
||
|
|
|
|
|
|
|
зываются абсолютными линейными деформациями. |
Отношение приращения длин отрез- |
|||||
ков к первоначальной длине называется относительной линейной деформацией: |
||||||
εx = |
dx , |
εy |
= |
dy , |
εz = |
dz . |
|
dx |
|
|
dy |
|
dz |
Изменение первоначально прямого угла между отрезками ab и ac после приложения нагрузки к телу, выраженное в радианах, представляет собой угловую деформацию γху в точ-
ке а в плоскости ху. Аналогично, γyz и γzх представляют собой угловые деформации в плоско-
стях yz и zx.

Деформации тела в каждой его точке по любым направлениям могут быть определены,
если известны линейные εx, εy, εz и угловые γху, γyz, γzх деформации. Линейные и угловые деформации – величины безразмерные.
1.9. Простейшие типы деформации бруса.
При произвольной форме тела его деформации могут быть весьма разнообразными.
Для бруса можно указать несколько простейших типов деформаций, возникающих при опре-
делённом способе приложения внешних сил.
Рассмотрим эти простейшие деформации бруса:
Рис. 1.10 1). Осевое растяжение или сжатие (рис. 1.10а).
При осевом растяжении или сжатии в поперечных сечения бруса возникают только продоль-
ные силы N. Брус, испытывающий растяжение или сжатие, называют стержнем. В зависи-
мости от вида конструкции сжатые стержни также называют стойками, колоннами, столбами. 2). Сдвиг (рис.1.10б).
При сдвиге в поперечных сечения бруса возникают только поперечные силы Q.
Деформации сдвига возникают в заклёпочных, болтовых, сварных, клеевых соединениях. 3). Кручение (рис.1.10в).
При кручении в поперечных сечения бруса возникают только крутящие моменты Mz. Стерж-
ни, работающие на кручение, называют валами. 4). Изгиб (рис.1.10г).
В поперечных сечения стержня возникают изгибающие моменты и поперечные силы, напри-
мер, Mx и Qy. Стержни, работающие на изгиб, называют балками.
В заключение отметим, что другие типы деформации стержней в большинстве случаев оказывается возможным рассматривать как комбинацию простых деформаций.
2. Стержень и его геометрические характеристики.
Стержень характеризуется осью и поперечным сечением.
Ось – линия соединяющая центры тяжести всех поперечных сечений стержня.
Поперечное сечение – плоская фигура, получающаяся при рассечении стержня плоскостью перпендикулярной его оси.
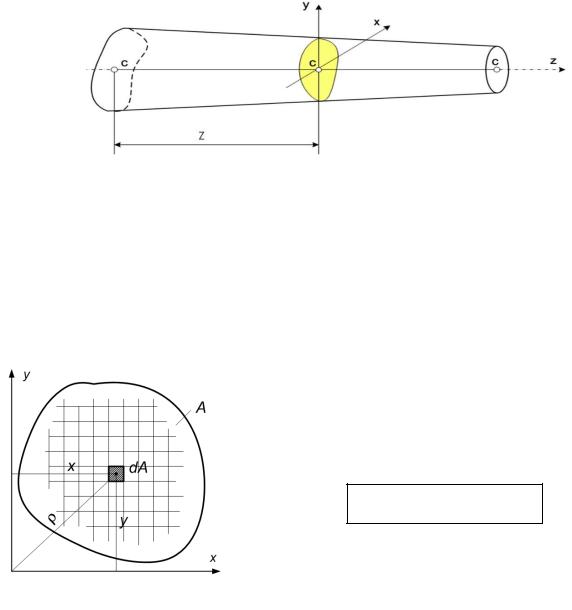
Ось стержня может быть прямолинейной или криволинейной.
Поперечное сечение может быть постоянным по длине стержня, но может быть и пере-
менным, как на рисунке.
При расчётах стержней на прочность используется не только площадь поперечного се-
чения стержней, но и более сложные геометрические характеристики сечений, которые необ-
ходимо ввести и научиться пользоваться ими.
2.1. Статические моменты сечений.
Разбиваем заданную фигуру на элементарные площадки dA
(рис. 2.1). Умножаем площадь каждой площадки на коорди-
наты их центра тяжести х и у. Интегрируя по площади сече-
ния, в итоге получим следующие результаты:
Sx = ∫ y dA , Sy = ∫ x dA .
A A
Sx и Sy называются статическими моментами сечения от-
носительно осей х и у.
Рис. 2.1
Для статических моментов можно указать следующие свойства:
статические моменты выражаются в см3, м3 и т. д.
статические моменты могут быть положительными, отрицательными и равными нулю.
статические моменты равны нулю относительно осей, проходящих через центр тяжести сечения – центральных осей.
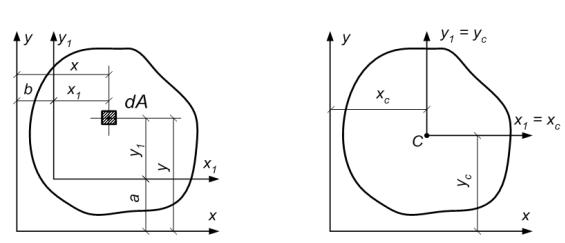
Рис. 2.2 |
Рис. 2.3 |
Установим зависимость между статическими моментами относительно пары парал-
лельных осей (рис. 2.2).
Sx1 = ∫ y1 dA ; Sx = ∫ y dA = ∫(y1 + a) dA = ∫ y1 dA + a ∫ dA = Sx1 + a × A .
A A A A A
Выполняя аналогичные вычисления для осей у и у1 , окончательно получим
Sx |
= Sx + a × A ; Sy |
= Sy |
+ b × A . |
|
1 |
|
1 |
Если оси х1 и у1 проходят через центр тяжести сечения (точка С, рис. 3), тогда
а = ус, b = хс и из полученных выше равенств будем иметь
Sxc = Sx - yc × A , Syc = Sy - xc × A .
Приравняв статические моменты Sxc и Syc нулю, получим формулы для определения поло-
жения центра тяжести сечения:
xc |
= |
Sy |
; yc = |
S |
x |
и Sx |
= yc × A ; Sy |
= xc × A . |
|
|
|||||||
A |
|
|
||||||
|
|
|
A |
|
|
|||
Из полученных формул следует:
статические моменты равны нулю относительно центральных осей;
оси симметрии являются центральными осями.
Если сечение можно разбить на ряд простых фигур (прямоугольники, треугольники,
круг, полукруг и т. д.), площади и центры тяжести которых известны, координаты центра тя-
жести сечения определяются по формулам:
xC |
= |
Σ ( Аi x i ); |
yC |
= |
Σ ( Аi y i ) . |
|
|
S Аi |
|
|
S Аi |
В отдельных случаях, когда заданное сечение нельзя разбить на простейшие, положе-
ние центра тяжести необходимо определять путём интегрирования.
