
9027
.pdfПолученную поверхность рассечём плоскостью,
параллельной |
координатной |
плоскости |
xOy и |
проходящей через фиксированную точку |
O (0, 0, z) |
||
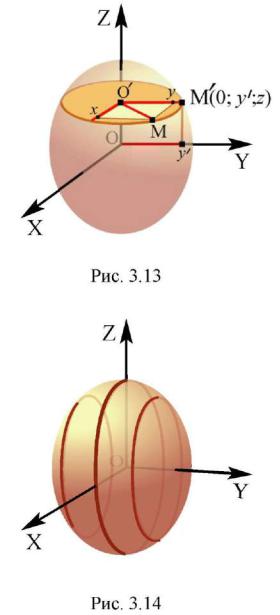
(рис. 3.13). |
|
|
|
Пусть |
M (x, y, z) |
– произвольная точка |
|
поверхности вращения, лежащая в плоскости сечения. Рассмотрим в плоскости yOz точку поверхности
M (0, y , z) . Её ордината по абсолютной величине равна
радиусу окружности, |
на |
которой |
|
лежит |
точка |
|||||
|
|
|
|
, поэтому x |
2 |
y |
2 |
y |
2 |
. |
M (x, y, z), т.е. O M |
|
O M |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Находящаяся в плоскости yOz точка M (0, y , z)
принадлежит и плоскости сечения, и исходному
эллипсу. |
Это |
|
означает, |
|
что |
её |
координаты |
||||||||||||||||
удовлетворяют уравнению |
|
y 2 |
|
|
z2 |
|
1. |
|
|||||||||||||||
|
b2 |
c2 |
|
|
|||||||||||||||||||
Подставляя в это уравнение выражение y через |
|||||||||||||||||||||||
x и y , получим |
|
x2 |
|
y2 |
|
z2 |
|
1. Это и есть искомое |
|||||||||||||||
|
b2 |
b2 |
|
c2 |
|
||||||||||||||||||
уравнение |
|
поверхности |
|
|
|
вращения, |
называемой |
||||||||||||||||
эллипсоидом вращения. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Если вращать эллипс |
|
|
y2 |
|
|
z2 |
1 вокруг оси Oy , |
||||||||||||||||
|
|
b2 |
|
c2 |
|||||||||||||||||||
получится |
другой эллипсоид |
|
вращения |
(рис. 3.14) с |
|||||||||||||||||||
|
|
x2 |
y2 |
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
уравнением |
|
|
|
|
|
1. |
|
|
|
|
|
|
|
||||||||||
c2 |
b2 |
c2 |
|
|
|
|
|
|
|
||||||||||||||
70
71
От этих примеров нетрудно перейти к алгоритму получения уравнения поверхности вращения по уравнению исходной кривой, если осью вращения служит одна из координатных осей. Если осью вращения служит ось Ox , то в уравнении кривой слагаемое с переменной x оставляем без изменения, а квадрат другой переменной заменяем суммой квадратов этой переменной и переменной, отсутствовавшей в уравнении. Аналогично – для других осей.
Итак, мы рассмотрели два способа формирования поверхностей, введя цилиндрические поверхности и поверхности вращения. При этом мы брали для изучения те случаи, которые оставляли нас в рамках поверхностей, определяемых уравнением (3.2). Чтобы полностью охватить всю панораму поверхностей второго порядка, будем двигаться теперь непосредственно от уравнений, выполняя построение методом сечений. Проследим, как образуются поверхности второго порядка, проявляясь постепенно по мере стыковки линий, являющихся сечениями поверхности плоскостями, параллельными координатным плоскостям.
3.5. Начнём с уравнения
|
x2 |
|
y2 |
|
z2 |
1 |
(3.3) |
|
a2 |
b2 |
c2 |
||||
|
|
|
|
|
|
|
|
Уравнение сечения этой поверхности координатной
плоскостью |
xOz получается, |
если |
в |
исходном |
||
уравнении |
(3.3) принять y 0 : |
x2 |
|
z2 |
1. |
По виду |
a2 |
c2 |
|||||
уравнения мы узнаём эллипс и можем изобразить его в соответствующей плоскости (рис. 3.15).
72
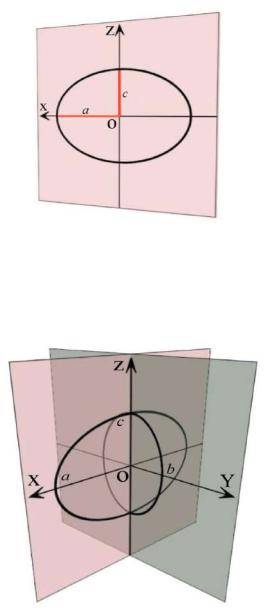
Рис. 3.15 |
|
|
|
|
|
При x 0 из (3.3) |
получаем уравнение |
y2 |
|
z2 |
1 |
b2 |
c2 |
||||
эллипса в плоскости |
yOz , имеющего те же точки |
||||
пересечения с осью Oz (рис. 3.16). |
|
|
|
|
|
Рис. 3.16
73
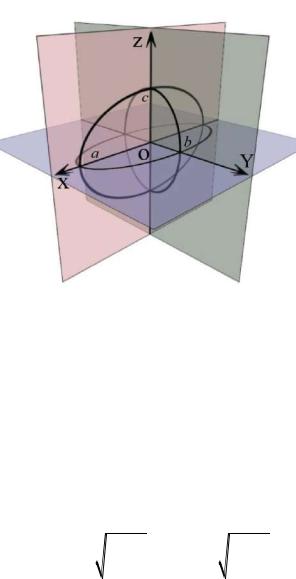
Рисунок дополняется эллипсом в плоскости xOy (рис.
3.17).
Рис. 3.17
Рассмотрим произвольную плоскость z h (где h – любое число), параллельную xOy . Сечение
исходной поверхности (3.3) этой плоскостью задаётся уравнением
|
x2 |
|
y2 |
1 |
h2 |
|
или |
|
|
|
x2 |
|
|
|
|
|
|
|
|
y2 |
|
|
1. |
|||||||
|
a2 |
b2 |
c2 |
|
|
|
a |
2 |
(1 |
|
h2 |
) |
|
b |
2 |
(1 |
h2 |
) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
c2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Тем самым при всех |
|
h |
c в сечении эллипсоида |
|||||||||||||||||||||||||
(3.3) |
плоскостями |
|
z h |
|
получаются |
|
|
эллипсы с |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
полуосями a |
|
a |
1 |
h2 |
|
и |
b |
b |
1 |
h2 |
|
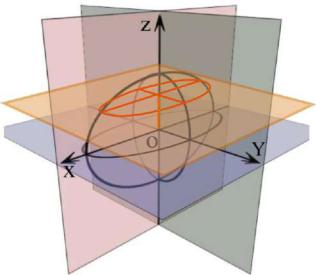
(рис.3.18). |
||||||||||||||||||
|
c2 |
c2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.18 |
|
|
|
|
|
Если |
|
h |
|
c , то ah a , bh b . При уменьшении |
|||
|
|
|
|
|
||||||
|
h |
|
полуоси |
|
|
|
ah и |
bh |
увеличиваются, достигая |
|
|
|
|
|
|
||||||
наибольших значений |
ah |
a и bh b , если |
h 0 . |
|||||||
Таким образом, «самый крупный» эллипс образуется в сечении координатной плоскостью xOy . Аналогичная картина получается в сечениях плоскостями, параллельными плоскостям xOz и yOz .
Рассмотрев h 2c , получим |
x2 |
|
y2 |
3. На |
a2 |
b2 |
плоскости нет точек, отвечающих такому условию. Следовательно, у поверхности, которую мы строим, нет пересечения с плоскостью z 2c , как и со всеми
плоскостями z h при |
h |
c , также и с плоскостями |
|
|
|
75
x h |
при |
|
|
h |
a |
или |
y h |
при |
h |
b . |
Плоскости |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z c |
и |
z c |
|
касаются |
поверхности, |
так |
как |
||||||||
уравнение |
|
|
x2 |
|
y2 |
|
0 |
задаёт точку. Общий |
вид |
||||||
|
a2 |
b2 |
|
||||||||||||
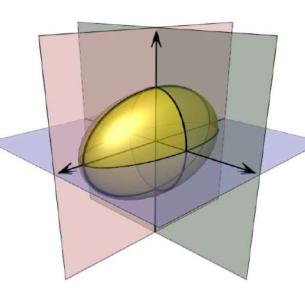
поверхности отражаем рисунком 3.19. Вполне естественно, что эта поверхность носит название «эллипсоид» – по названиям сечений.
|
Рис. 3.19 |
|
|
Эллипсоид |
обладает |
тремя |
взаимно |
перпендикулярными плоскостями симметрии (при данном выборе осей они совпадают с координатными плоскостями). Величины a , b и c называются полуосями эллипсоида. Если две из трёх полуосей одинаковы, то, эллипсоид становится эллипсоидом
вращения. Если |
a b c , то уравнение (3.3) |
определяет сферу. |
|
3.6. Далее рассмотрим уравнение
|
|
x2 |
|
y2 |
|
z2 |
|
|
|
|
|
|
|
|
|
|
1. |
|
(3.4) |
|
|
a2 |
b2 |
c2 |
|
||||
В сечениях координатными плоскостями |
xOz и yOz |
||||||||
поверхности, |
определяемой |
этим |
уравнением, |
||||||
получаются гиперболы, а в сечениях, параллельных координатной плоскости xOy – эллипсы (рис. 3.20). В
целом поверхность выглядит, как бесконечная трубка, расширяющаяся в обе стороны от горлового эллипса (рис. 3.21). Она носит название «однополостный гиперболоид».
Эта поверхность обладает тремя плоскостями симметрии (при данном выборе осей они совпадают с координатными плоскостями). Величины a , b и c называются полуосями однополостного гиперболоида. Если a b , то однополостный гиперболоид становится
поверхностью вращения |
и может |
быть получен |
|||
вращением гиперболы |
y2 |
|
z2 |
1 |
вокруг оси Oz , |
b2 |
c2 |
||||
которую она не пересекает.
Однополостный гиперболоид обладает интересным геометрическим свойством, которое можно обнаружить, если представить уравнение (3.4) в виде
|
x2 |
|
z2 |
1 |
y2 |
|
a2 |
c2 |
b2 |
||
или, эквивалентно, |
|
|
|
|
|
x |
|
z x |
|
z |
|
|
|
y |
|
y |
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
. |
(3.5) |
|
|
|
|
|
|
||||||||||||
a |
|
c a |
|
c |
|
|
|
b |
|
b |
|
||||||
|
|
|
|
|
|
|
|
|
77 |
|
|
|
|
|
|
|
|
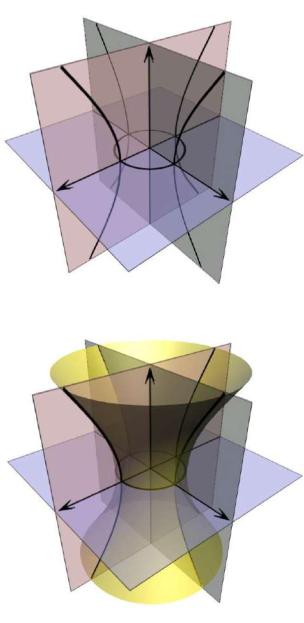
Рис. 3.20
Рис. 3.21
78
Наряду с этим уравнением рассмотрим две системы линейных уравнений
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||
|
|
|
x |
|
|
|
z |
|
|
|
|
|
|
|
y |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
a |
|
|
|
c |
|
|
|
|
|
b |
|||||||||
|
|
x |
|
|
|
z |
|
|
|
|
|
y |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
a |
|
|
|
c |
|
|
|
|
|
b |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
x |
|
|
z |
|
|
|
|
|
|
|
y |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
a |
|
|
c |
|
|
|
|
b |
||||||||||
|
|
|
x |
|
|
|
z |
|
|
|
|
|
|
|
y |
||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
a |
|
|
c |
|
|
|
|
b |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
(3.6)
(3.7)
В них и - некоторые числа, не равные
одновременно нулю. При фиксированных значениях и уравнения (3.6) или (3.7) задают в пространстве конкретную прямую как пересечение плоскостей. Меняя и , мы получаем бесконечную систему
прямых. Если перемножить уравнения (3.6) или (3.7), то получится уравнение (3.5). Это означает, что каждая из прямых лежит целиком на однополостном гиперболоиде. Можно доказать, что через каждую точку однополостного гиперболоида проходит две прямые, определяемые системами (3.6) и (3.7). То есть прямые (называемые прямолинейными образующими однополостного гиперболоида) покрывают его поверхность целиком.
Поверхности, составленные из прямых, называют линейчатыми. Ясно, что конусы и цилиндры относятся к этому классу. Но для однополостного гиперболоида
79
