
9027
.pdf
Рис. 3.5
60

Войдя в соприкосновение с аналитической геометрией пространства, можно иначе взглянуть на первоначальную задачу. Мы с отцом договорились, что горизонтальными сечениями бутылки всюду будут эллипсы, а в верхней части (в горлышке) – окружности. В её средней части от основания начинается плавное сужение, а потом оно переходит в занимающее наиболее протяжённую часть длины объёма расширение с небольшим раствором (рис.3.6).
Рис. 3.6
Для определения объёма по формуле, полученной в первой главе, всё это должно быть отражено зависимостью параметров горизонтальных эллипсов от высоты. То есть нужно связать между собой три координаты точек, расположенных в пространстве на поверхности определённой формы – такой формы, какой она нам виделась. Получается, что нам требовалось уравнение поверхности. Но где же я мог взять уравнение поверхности бутылки?
61

3.2. Ранее я встречался только с уравнениями так называемых поверхностей второго порядка. Они носят такое название именно по виду уравнений, в которые входят вторые степени текущих координат или их взаимные произведения. В общем виде уравнение поверхности второго порядка выглядит так:
|
Ax2 By2 |
Cz2 2Dxy 2Exz |
, |
(3.2) |
|
2Fyz 2Gx 2Hy 2Kz L 0 |
|
|
|
|
|
|
|
|
где коэффициенты |
A, B,C, D, E , F ,G , H , K и L |
— |
||
любые действительные числа, но, по крайней мере, одно из чисел A, B,C, D, E или F отлично от нуля (т.е.
A2 B2 C2 D2 E2 F 2 0 ). В таком уравнении
учтены все возможные слагаемые. Если включить в него любые другие функции, оно, по определению, перестанет быть уравнением второго порядка.
Такой выбор представлялся для меня удачным, поскольку сечениями поверхностей второго порядка являются кривые второго порядка, к которым относится и эллипс. Также как и для кривых второго порядка, для поверхностей второго порядка существует полная классификация.
С помощью подходящего параллельного переноса и поворота осей координат (теперь уже выполняемых в пространстве) любое уравнение второго порядка вида (3.2) может быть приведено к одному из семнадцати видов. Этим уравнениям в пространстве отвечают классические поверхности: эллипсоид, однополостный и двуполостный гиперболоиды, конус, эллиптический и гиперболический параболоиды, а также целая группа поверхностей, называемых цилиндрическими. С изучения последних мы и начнём.
62

3.3. Поверхность, состоящая из параллельных прямых (так называемых образующих), проходящих через каждую точку заданной линии L (направляющей), называется цилиндрической поверхностью. Образно можно представить, что цилиндрические поверхности образуются движением прямой, которая перемещается в пространстве вдоль кривой L , сохраняя постоянное направление (рис. 3.7).
Рис. 3.7
В качестве направляющей цилиндрической поверхности рассмотрим расположенную в плоскости
xOy линию L , |
которая |
задаётся |
уравнением |
F(x, y) 0 . Пусть |
M1 (x0 , y0 ,0) |
– произвольная точка |
|
направляющей (рис. 3.8). Тогда F (x0 , y0 ) 0 . |
|||
Рассмотрим |
цилиндрическую |
поверхность, |
|
образующие которой параллельны координатной оси
Oz . Если такая образующая проходит |
через |
M1 (x0 , y0 ,0) , то абсциссы всех её точек равны |
x0 , а |
ординаты равны y0 . |
|
63 |
|
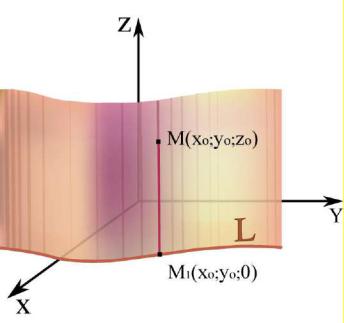
Поэтому координаты произвольной точки M (x0 , y0 , z0 ) этой образующей тоже удовлетворяют
уравнению F(x, y) 0 при любом значении z0 . Поскольку точка выбиралась
произвольно, то можно утверждать, что координаты всех точек цилиндрической поверхности удовлетворяют уравнению F (x, y) 0 .
Рис. 3.8
Ясно, что уравнение вида F(x, z) 0, не содержащее переменной y , задаёт цилиндрическую поверхность с образующими, параллельными оси уравнение вида F( y, z) 0 задаёт цилиндрическую поверхность с образующими, параллельными оси Ox .
64
Если направляющей цилиндрической поверхности является кривая второго порядка, то поверхность называется цилиндрической поверхностью второго порядка (или цилиндром второго порядка). В
зависимости от конкретного вида уравнения получаются различные типы цилиндров второго порядка. Их названия соответствуют названиям направляющих линий L .
Например, |
уравнение |
x2 |
|
y2 |
1 задаёт в |
|
a2 |
b2 |
|||||
пространстве |
так |
называемый |
эллиптический |
|||
цилиндр. Это цилиндрическая поверхность с образующими, параллельными оси Oz . Её направляющей является эллипс, расположенный в плоскости xOy . Такие же эллипсы получаются во всех сечениях поверхности плоскостями, параллельными координатной плоскости xOy (рис. 3.9).
Частным случаем эллиптического цилиндра является круговой цилиндр. Его каноническое
уравнение имеет вид x2 + y2 = R2 .
Уравнение вида y2 = 2 px определяет в
пространстве параболический цилиндр. На рисунке 3.10 изображен параболический цилиндр,
соответствующий уравнению x2 2 py .
|
x2 |
|
y2 |
|
|
Уравнение вида |
|
- |
|
= 1 |
определяет в |
a2 |
b2 |
||||
пространстве гиперболический цилиндр. На рисунке
3.11изображен гиперболический цилиндр,
соответствующий уравнению |
y2 |
|
x2 |
1. |
b2 |
a2 |
|||
65 |
|
|
|
|
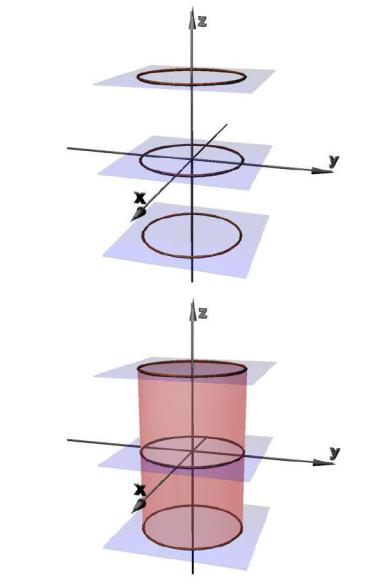
Рис. 3.9
66
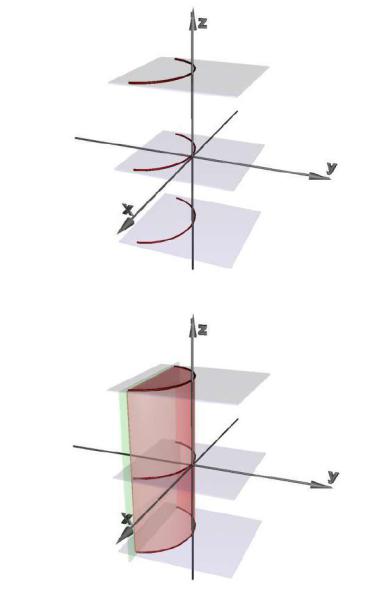
Рис. 3.10
67
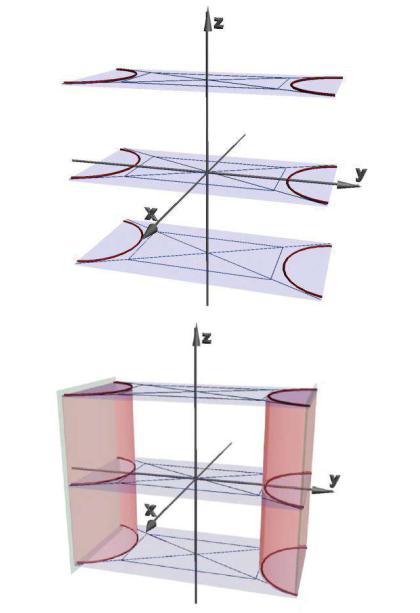
Рис. 3.11
68
3.4. Возможно представить другой способ формирования поверхностей – если какую-либо плоскую линию L (называемую образующей) вращать вокруг прямой (оси вращения), расположенной в плоскости этой линии. Получится так называемая поверхность вращения. Примером служит сфера: её можно рассмотреть как поверхность, образованную вращением полуокружности вокруг её диаметра.
Получим уравнение поверхности вращения в том случае, когда образующая лежит в одной из координатных плоскостей. В качестве оси вращения при этом рассмотрим одну из координатных осей, расположенных в той же плоскости.
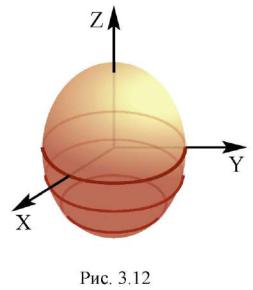
Будем вращать расположенный в плоскости yOz
эллипс с уравнением |
y2 |
|
z2 |
1 |
вокруг |
b2 |
c2 |
координатной оси Oz (рис. 3.12).
69
