8908

Вершина ориентированного графа называется истоком, если в нее не входит ни одна дуга, то есть ее полустепень захода равна нулю deg+ (v) =0.

Вершина ориентированного графа называется стоком, из нее не выходит ни одной дуги, то есть ее полустепень исхода равна нулю deg− (v) =0.

Используя матрицу смежности легко определить локальные степени вер-

шин графа: сумма элементов матрицы по строке равна локальной степени соот-

ветствующей вершины. Для орграфов по строке определяются полустепени ис-

хода, по столбцам – полустепени захода.

Операции над графами.

Для получения новых графов можно использовать операции над графами.

Существуют два вида операций – локальные, при которых заменяются, удаля-

ются или добавляются отдельные элементы графа, и алгебраические, когда но-

вый граф строится по определенным правилам из нескольких имеющихся.

Локальные операции – это удаление и добавление ребра или вершины,

стягивание и подразбиение ребра.

При удалении ребра сохраняются все вершины графа и все его ребра,

кроме удаляемого. Обратная операция – добавление ребра.

При удалении вершины вместе с вершиной удаляются и все инцидентные ей ребра. При добавлении вершины к графу добавляется новая изолированная вершина.

Операция стягивания ребра определяется следующим образом. Вершины a и b удаляются из графа, к нему добавляется новая вершина c и она соединяет-

ся ребром с каждой вершиной, с которой была смежна хотя бы одна из вершин

a, b.

Операция подразбиения ребра действует следующим образом. Из графа удаляется это ребро, к нему добавляется новая вершина и два новых ребра (a,c)

и (b,c).

Определение. Два графа G1 (V1, E1 ) и G2 (V2 , E2 ) называются равными,

52

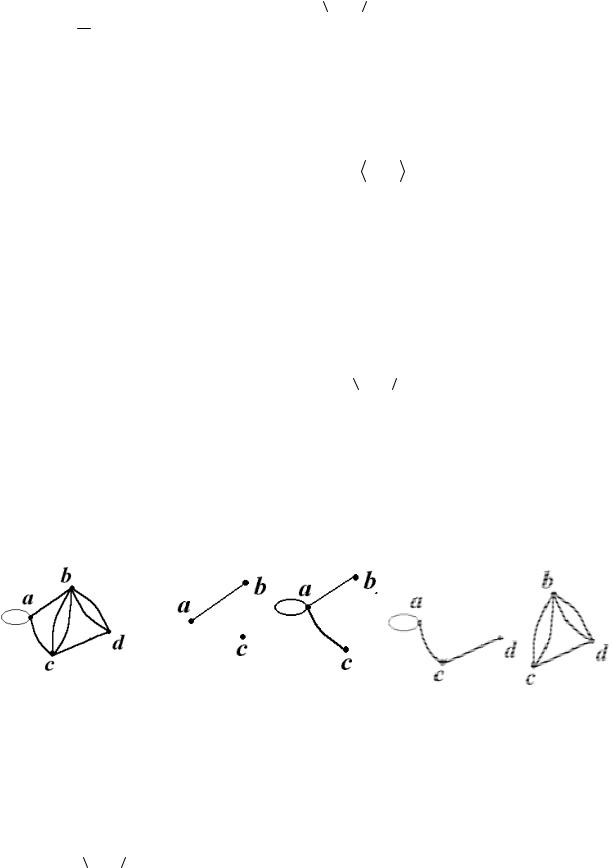
если V1 = V2 и E1 = E2 . Обозначение: G1 = G2 .

Определение. Пусть задан граф G = 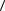V , E 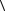. Дополнением графа G назы-

вается граф G с теми же вершинами, что и граф G , и с теми и только теми реб-

рами, которые необходимо добавить, чтобы получить полный граф. Граф, не являющийся полным, можно преобразовать в полный с теми же вершинами,

Частичный граф содержит только часть ребер (дуг) исходного графа. Так,

карта главных дорог России – частичный граф карты шоссейных дорог России.

Частным, но важным типом частичных графов являются подграфы.

Граф Н является подграфом графа G = 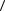V , E , если V(H) V и E(H) E, и

при этом любое ребро из Е, соединяющее две вершины из V(H), принадлежит

E(H) (т.е. ребрами подграфа являются все ребра из G , оба конца которых лежат в H). Так, карта шоссейных дорог Нижегородской области России является подграфом графа «Карта шоссейных дорог Российской федерации».

Рис 3.9. Пример частичного графа и подграфа.

Клика графа – это его максимально полный подграф.

Подграф называется остовным подграфом (суграфом) если множество

его вершин совпадает с множеством вершин самого графа. Остовной подграф

Н графа G = V , E получается из исходного графа удалением только ребер без

53

удаления вершин.

Подграфом, порождённым множеством вершин U называется подграф,

множество вершин которого – U, содержащий те и только те рёбра, оба конца которых входят в U. Порожденный подграф Н графа G = V , E 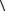получается из исходного графа удалением вершин и всех ребер, инцидентных удаленным вершинам.

торого V = V1 ÈV2 , множество ребер E = E1 È E2 .

Определение. Пусть заданы два графа G1 (V1, E1 ) и G2 (V2 , E2 ) . Пересе-

чением G1 Ç G2 называется граф, множество вершин которого V = V1 ÇV2 ,

множество ребер E = E1 Ç E2 .

Определение. Соединение (сумма) графов G1 + G2 состоит из G1 È G2 и

всех ребер, соединяющих вершины множества V1 с вершинами множества V2 .

Определение. Произведением графов G1 ´ G2 называется граф с множе-

ством вершин V1 ´V2 , при этом вершины u = (u1 ,u2 ) и v = (v1, v2 ) смежны в

G1 ´ G2 тогда и только тогда, когда u1 = v1 и вершина u2 смежна с v2 в графе

G2 или u2 = v2 и вершина u1 смежна с v1 в графе G1 .

Рис 3.10. Примеры операций над графами.

Определение. Два графа G1 (V1, E1 ) и G2 (V2 , E2 ) называются изоморф-

ными, если существует биекция (взаимно однозначное отображение) ϕ множе-

54

ства V1 на множество V2 такое, что для любых двух вершин a V1 , b V2

(a,b) E1 (ϕ (a),ϕ (b)) E2 .

Тот факт, что графы G1 и G2 изоморфны, записывается следующим обра-

зом: G1 G2 .

Некоторые свойства изоморфизма графов:

1)число ребер и число вершин у изоморфных графов должно быть оди-

наковым;

2)при всяком изоморфизме графов G и G' соответствующие друг другу вершины должны иметь одинаковую степень.

Например, все три графа на рисунке 3.11 изоморфны друг другу (изоморфизм определяется нумерацией вершин).

Рис. 3.11. Изоморфные графы На рисунках 3.12 представлены попарно неизоморфные графы.

Рис. 3.12. Неизоморфные графы

55

Маршруты, цепи и циклы в графах. Связные графы. Метрические

соотношения.

Маршрут в графе G(V,E) – это чередующаяся последовательность вер-

шин и рёбер v1, e1, v2 , e2 ,…, vn , en , в которой любые два соседних элемента

инцидентны.

Говорят, что маршрут соединяет вершины v1 и vn , они называются со-

ответственно началом и концом маршрута, вершины v2 ,…, vn−1 называются

промежуточными. Маршрут называется замкнутым или циклическим, если v1 = vn , иначе маршрут называется открытым.

Длиной маршрута называется число ребер в нем. Для любой вершины vi тривиальным маршрутом, вообще не содержащим ребер, является маршрут

из vi в vi .

Маршрут, в котором все ребра разные, называется цепью. Цепь, не пере-

секающая себя, т.е. не содержащая повторяющихся вершин, называется про-

стой цепью.

Цикл – это замкнутая цепь. Простым циклом в графе называется цикл,

не проходящий ни через одну из вершин графа более одного раза.

Граф, не содержащий циклов, называется ациклическим.

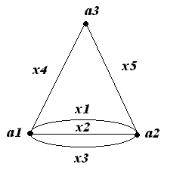
Проиллюстрируем введенные понятия для графа на рис. 3.13.

a1x1a2 x5a3 x4a1 и a2 x5a3 x4a1x3a2 .

56

Две вершины графа A и B называются связанными, если в графе сущест-

вует маршрут с концами A и B. Связанные маршрутом вершины связаны также и простой цепью.

Граф называется связным, если в нем для любых двух вершин имеется маршрут, соединяющий эти вершины.

В связном графе имеется только одна компонента связности – весь граф.

Компоненты связности можно определить также как связные подграфы данного графа.

Ребро, при удалении которого увеличивается число компонент связности,

называется перешейком (или мостом).

Пусть G – ориентированный граф. В орграфе последовательность ребер,

в которой конец каждой дуги совпадает с началом следующей, называется пу-

тем (в нем ребра проходят по их ориентации). Путь называется ориентиро-

ванной цепью, если каждое ребро встречается в нем не более одного раза, и

простой ор-цепью, если каждая вершина инцидентна не более чем двум его ребрам. Контур – замкнутый путь в орграфе.

Если в ориентированном графе нельзя «пройти» от одной вершины до другой вершины, то расстояние между ними называют бесконечным.

Пусть vi и v j – вершины орграфа G. Вершина vi достижима из v j ,

если существует путь с началом vi и концом v j . Любая вершина достижима сама из себя. Вершины vi и v j сильно связаны, если они достижимы одна из другой.

Например, для графа, изображенного на рисунке 3.14, вершины v2 и v3

сильно связаны, вершины v1 и v4 сильно связаны, вершина v6 достижима из v1, но вершина v1 недостижима из v6 .

57

Рис. 3.14.

Орграф называется связным, если он связен без учета ориентации дуг, и

сильно связным, если из любой вершины vi в любую вершину v j существует

путь.

Достижимость в графе описывается матрицей достижимости

Матрица сильной связности ориентированного графа G − квадратная

матрица S(G)=[sij] порядка n, элементы которой равны:

Вершина является шарниром, если ее удаление вместе с инцидентными ребрами увеличивает количество компонент связности.

Пример 3.4. Определим шарниры в графе на рисунке 3.15.

Рис. 3.15.

Граф на рис. 3.15 связный, то есть представляет собой одну компоненту связности. Удалим вершину 2 вместе с инцидентными ребрами (строку 2 и

столбцы 3, 4, 5 в матрице инцидентности). В графе останутся три ребра: 13, 15

58

и 46. Ребра 13 и 15 образуют одну компоненту связности, а ребро 46 – другую.

Удаление вершины 2 увеличило количество компонент связности, поэтому вершина 2 является шарниром в графе.

Расстоянием между двумя вершинами графа называется длина крат-

чайшего пути, соединяющего эти вершины. Расстояние между вершинами a и b

обозначается через d (a,b). Если в графе нет маршрута или пути, соединяюще-

го a и b, то есть эти вершины принадлежат разным компонентам связности, то

расстояние между ними считается бесконечным.

Расстояние от данной вершины a до наиболее удаленной от нее вершины называется эксцентриситетом вершины a и обозначается через e(a). Таким

образом,

Вершину с наименьшим эксцентриситетом называют центральной, а

вершину с наибольшим – периферийной. Множество всех центральных вер-

шин называется центром графа. Сама величина наименьшего эксцентриситета называется радиусом графа и обозначается через r(G), а величина наибольше-

имеет полный граф – его диаметр равен 1. Среди связных графов с n вершина-

ми наибольший диаметр, равный n −1, имеет цепь Pn .

Пример 3.5. Для графа G, изображенного на рисунке 3.16, найдем радиус,

диаметр и центры.

Рис. 3.16.

Решение. Чтобы определить центры, радиус, диаметр графа G, найдем

59

матрицу D(G) расстояний между вершинами графа, элементами dij которой бу-

дут расстояния между вершинами vi и v j . Для этого воспользуемся графиче-

ским представлением графа.

Заметим, что матрица D(G) симметрична относительно главной диагона-

ли. С помощью полученной матрицы для каждой вершины графа G определим наибольшее удаление по формуле вычисления эксцентриситета e(vi ): e(v1 ) = 3,

e(v2 ) = 2 , e(v3 ) = 2 , e(v4 ) = 2 , e(v5 ) = 3 . Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит,

r(G) = 2 и diam(G) = 3, центрами являются вершины v2 , v3 , v4 .

Обходы графа (эйлеровы и гамильтоновы графы).

Определение. Эйлеров цикл – цикл, проходящий через все ребра графа (в

эйлеровом цикле одна вершина может проходиться несколько раз). Граф, кото-

рый имеет эйлеров цикл, называется эйлеровым графом.

Эйлерова цепь (путь, цикл, контур) – цепь (путь, цикл, контур), содержа-

щая все ребра (дуги) графа по одному разу. Граф, который имеет эйлерову цепь, называется полуэйлеровым графом (рис. 3.17).

Эйлер сформулировал и доказал теоремы (необходимое и достаточное условие существования эйлерова цикла и эйлеровой цепи).

60