
- •Лабораторная работа n102 методы обработки физических измерений Измерение физических величин
- •Классификация ошибок измерений
- •Методы учета инструментальных погрешностей
- •Основные понятия теории вероятностей
- •Случайные величины
- •Параметры распределения случайных величин
- •Непрерывные случайные величины
- •Гипотеза о функции нормальногораспределения случайных ошибок
- •Интеграл вероятностей
- •Ошибка среднего арифметического
- •Доверительный интервал и доверительная вероятность (классическая оценка)
- •Выборочной метод
- •Значения коэффициентов Стьюдента
- •Погрешности косвенных измерений
- •Использование косвенных измерения в методе малых выборок
- •Правила обработки результатов измерений
- •Графическое представление результатов измерений
- •Лабораторная работа 102 измерение линейных размеров оптиметром икг
- •Измерения и обработки результатов измерений
Значения коэффициентов Стьюдента
|
n δ |
0,9 |
0,95 |
0,99 |
0,999 |
|
1 |
2 |
3 |
4 |
5 |
|
2 3 4 5 6 7 8 9 10 ∞ |
6,31 2,92 2,35 2,13 2,02 1,94 1,90 1,86 1,83 1,65 |
12,71 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 1,96 |
63,66 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 2,58 |
636,62 31,60 12,84 8,61 6,86 5,96 5,40 5,04 4,78 3,29 |
Например,
задавая доверительную вероятность δ
=0.95, по числу проведенных измерений n=5
по табл. 2 можно найти
![]() =
2,78. Тогда, определив предварительно
=
2,78. Тогда, определив предварительно![]() по формуле (35), найдем погрешность ∆X:
по формуле (35), найдем погрешность ∆X:
![]() (41)
(41)
Выражение (41) ввиду малого объема информации дает границы доверительного интервала более широкими.
Результат измерения можно представить в виде:
![]() при
δ=0,95, n=5.
(42)
при
δ=0,95, n=5.
(42)
Конечно, оценка (42) еще не дает представления об общей погрешности измерения, в которую входит и систематическая ошибка.
Совместный
учет случайных
![]() и систематических
и систематических![]() ошибок можно произвести по формуле
ошибок можно произвести по формуле
![]()
При
этом следует принять во внимание, что
![]() всегда имеет максимальное значение.
Максимальное же значение случайных
ошибок равно 3σ . Следовательно, для их
равноправного учета необходимо
предположить, что приборная погрешность
β (или ∆пр)
равна утроенной дисперсии распределения
погрешностей прибора 3σпр
,т.е. погрешности соответствующей
надежности δ =0.997. Тогда за систематическую
ошибку можно принять
всегда имеет максимальное значение.
Максимальное же значение случайных
ошибок равно 3σ . Следовательно, для их
равноправного учета необходимо
предположить, что приборная погрешность
β (или ∆пр)
равна утроенной дисперсии распределения
погрешностей прибора 3σпр
,т.е. погрешности соответствующей
надежности δ =0.997. Тогда за систематическую
ошибку можно принять
![]() и общая погрешность выразитсясоотношением
и общая погрешность выразитсясоотношением
![]() (43)
(43)
Коэффициенты
Стьюдента для проведенного числа
измерений
![]() и бесконечного числа измерений
и бесконечного числа измерений![]() находят по табл.2 для одной и той же
заданной надежности
δ.
находят по табл.2 для одной и той же
заданной надежности
δ.
Погрешности косвенных измерений
Часто
приходится вычислять искомую величину
по результатам измерений других величин,
связанных с этой величиной определенной
функциональной зависимостью. Например,
объем шара
![]() можно вычислить, измерив его радиусR
. Также измерения называются косвенными.
можно вычислить, измерив его радиусR
. Также измерения называются косвенными.
Рассмотрим конкретный пример. Допустим, что величины Х0, У0 и U0 связаны равенством
![]() .
(44)
.
(44)
Непосредственно измеряются величины Х0 и У0, и по этим измерениям мы судим об U0, считая
![]() (45)
(45)
измерением величины U0.
Предполагается, что измерения Хi и yi независимы друг
от
друга, и распределены нормально с
дисперсиями
![]() и
и![]() Задача
заключается в том, как по известным
значениям
Задача
заключается в том, как по известным
значениям![]() и
и![]() определить
определить![]() и
и![]() .
.
Очевидно,
что погрешность косвенного измерения
![]() обусловлена
погрешностями отдельных измерений
обусловлена
погрешностями отдельных измерений
![]() и
и![]() .
Поэтому выражение (45) можно переписать
в виде:
.
Поэтому выражение (45) можно переписать
в виде:
![]() (46)
(46)
Вычитая почленно левые и правые части уравнений (46) и (44). для погрешности косвенного измерения получим:
![]() (47)
(47)
Тогда для дисперсии результатов косвенного измерения можно записать выражение:
![]()
Здесь
член
![]() , так как любое произведение
, так как любое произведение![]() может быть с равной вероятностью или
положительным, или отрицательным.
может быть с равной вероятностью или
положительным, или отрицательным.
Учитывая,
что
![]() и
и![]()
получим
![]() (48)
(48)
или
![]() (49)
(49)
Равенство (49) определяет соотношение средних квадратичных ошибок прямых и косвенных измерений. Это выражение для частного случая имеет весьма общий характер и называется законом сложения дисперсий.
Следовательно, при измерении нескольких неизвестных величин складываются дисперсии этих величин (не ошибки, а именно дисперсии).
Средние
квадратичные ошибки средних арифметических
![]() связаны
аналогичным образом
связаны
аналогичным образом
![]() (50)
(50)
Рассмотрим общий случай, когда u - функция двух переменных х и y:
![]() (51)
(51)
Ошибки
в величинах х и у такова:
![]() ,
где Х0
и У0
- истинные значения величин Х в У. Тогда
для результата отдельного измерения
можно записать
,
где Х0
и У0
- истинные значения величин Х в У. Тогда
для результата отдельного измерения
можно записать
![]() (52)
(52)
Если
‘та функция непрерывна и имеет
производные, то ее можно разложить в
ряд Тейлора. Рассматривая только члены
c
нулевыми и первыми степенями малых
погрешностей
![]() и
и![]() ,
получим:
,
получим:
![]()
или
поскольку
![]()
![]() (53)
(53)
Частные производные здесь вычисляются при Х=Х0 и У=У0. Запишем выражение для дисперсии результатов косвенного измерения:
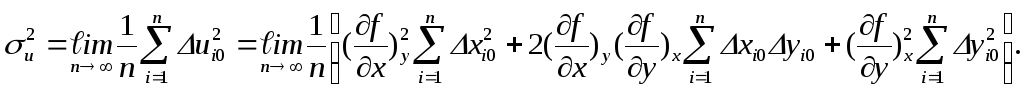
Учитывая, что
![]() и
и
![]()
получим
![]() (54)
(54)
или
![]() (55)
(55)
Для относительной погрешности косвенного измерения
![]()
учитывая,
что
![]() и
и![]() получим:
получим:
![]() (56)
(56)
