Доверительный интервал и доверительная вероятность (классическая оценка)

Доверительным называют интервал () , который с заданной доверительной вероятностью δ содержит истинное значение Х₀ искомой величина; () и () являются доверительными границами интервала. При этом обычно задаются стандартными значениями доверительной вероятности 0,9; 0,95; 0.99; 0,999.

Доверительной вероятностью называют вероятность δ того, что истинное значение Х₀ измеряемой величины содержится внутри заданного доверительного интервала (). При этом δ выражают либо в долях единицы (доверительная вероятность), либо в процентах (надежность).

В классической теории ошибок неизвестные σ и заменяют их приближенными значениямии; вычисленными из опытных данных по формулам (34) и (35). Доверительную вероятность и доверительный интервал определяют по табл.1 интеграла вероятностей согласно уравнению (27). полагая

(36)

При этом результат измерений принято записывать в краткой символической форме:

(37)

Эту запись следует понимать в том смысле, что истинное значение Х₀ с заданной вероятностью δ находится внутри доверительного интервала ().

Классическим методом оценки точности результата измерений можно пользоваться лишь при выборке с большим числом (20) измерений.

Выборочной метод

В классическом методе для нахождения границ доверительного интервала при заданной надежности δ или наоборот, для определения δ по заданному ΔХ необходимо знать точное значение дисперсии σ² генеральной совокупности измерений. Из опытных данных нам известна лишь дисперсия случайной выборки из этой генеральной совокупности. А так как рассеяние результатов относительно средней арифметическойвсегда меньше рассеяния относительно истинного значения Х₀, то

Если мы для оценки доверительного интервала или доверительной вероятности воспользуемся табл.2 интеграла вероятностей, полагая при малом числе измеренийп, то найдем неверные значения ΔХ (заниженные) и δ (завышенные). В этом заключается недостаток классического метода оценки точности результата измерений.

Оказывается, что и при неизвестной дисперсии σ^г можно дать точную оценку приближенного равенства Хр , если исходить не из распределения величины, а из распределения другой случайной величины

(38)

Распределение случайной величины t_δ(n) получил английский химик и математик В.С. Госсет, публиковавший свои работы под псевдонимом "Стьюдент" (студент). Плотность вероятности распределения Стьюдента имеет вид:

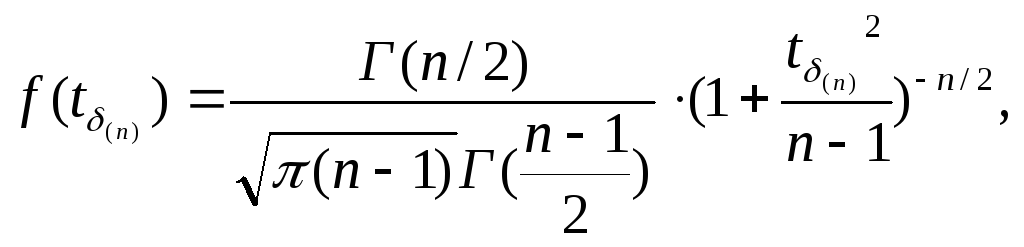(39)

где Г (n) - гамма функция Эйлера, являющаяся обобщением понятия факториала.

На рис.5 приведены графика распределения Стьюдента для разных значений п. При распределение (39) переходит в распределение Гаусса (23) и единичной дисперсией.

Распределение Стьюдента. аналогично распределению Гаусса, позволяет производить оценку точности результата измерений согласно выражению

(40)

Только .теперь вместо 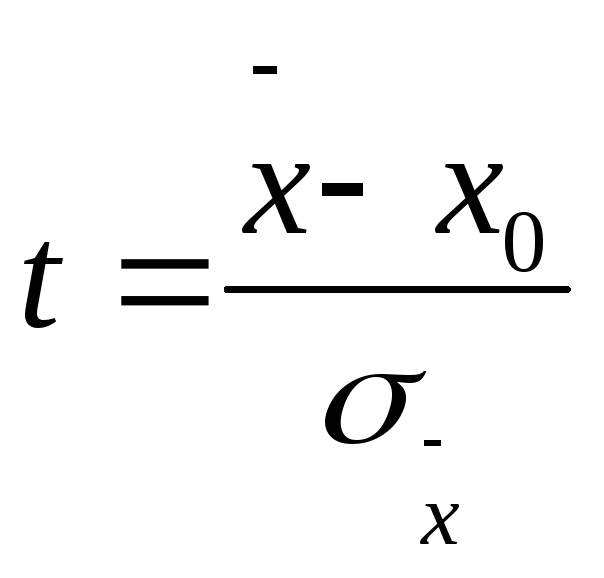вводится коэффициент Стьюдентазависящий от числа измеренийn и величины надежности δ .

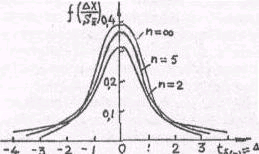
Рис. 5

Для коэффициентов Стьюдента составлены подробные таблицы. Ниже приводится небольшая часть из них.

Таблица 2