§5. Выпуклое программирование.

Общая задача выпуклого программирования заключается в минимизации функции

при условиях:

то есть в отыскании средних точек области решений Ω такой точки , для которой

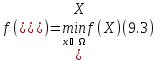
где – выпуклые гладкие функции.

Приведем общую задачу к каноническому виду. С этой целью в задачу выпуклого программирования вводится дополнительная переменная и дополнительное ограничение

Тогда задача (9.1) - (9.2) будет эквивалентной задаче минимизации линейной формы

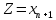
при ограничениях:

которая называется канонической.

Или

где функции 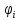– гладкие и выпуклые. Для решения задачи (9.1) - (9.2) и , следовательно, (9.4) - (9.5) можно использовать метод наискорейшего спуска.

Квадратичное программирование.

Задача квадратичного программирования заключается в минимизации функции

при ограничениях

то есть в отыскании среди точек области решения Ω такой точки , для которой

Матрица симметрична и положительно определенная. Функция– выпуклая.

1. Задачу (9.16) –(9.17) можно решить, применив алгоритм выпуклого программирования с некоторыми отличиями.

а) Направление наискорейшего спуска из точки определяют из следующей задачи линейного программирования

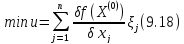
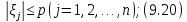
б) Значение шага вычисляются по формуле

Геометрическая интерпретация и графический способ решения задачи квадратичного программирования

Дана задача квадратичного программирования

(9.35)

Линейная система ограничений описывает некоторую выпуклую многоугольную область на плоскости (. Множество всех точек X(,), в которых целевая квадратичная функция принимает заданное значение, лежит на линии уровня данной функции. Эти линии являются кривыми, обрауземыми при пересечении поверхности (9.35) с плоскостью. Форма этих кривых зависит от вида квадратичной функции.

Рассмотрим простейшие случаи:

1.

В этом случае линии уровня являются концентрическими окружностями. Чтобы определить центр этих окружностей, необходимо привести квадратичную функцию к виду

Пример. Найти минимум и максимум функции

при условиях:

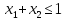
Решение. Приведём уравнение квадратичной функции к каноническому

виду 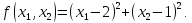Целевая функция представляет семейство концентрических окружностей с центром в точке

Рис. 9.1 Графическое решение задачи квадратичного программирования. Линии уровня – окружности.

Построим область допустимых решений. Минимальное значение соответствует наименьшему радиусу окружности и достигается в точке, в которой окружность касается многоугольника О AB. Это точка А (0,1). Максимальное значение соответствует наибольшему радиусу и достигается в наиболее удаленной от точки вершине многоугольника O AB. Это точка B(1,0). Следовательно,

2.

В этом случае линии уровня являются эллипсами с центрами в точке и канонический вид квадратичной функции будет

При этом полуоси эллипса соотносятся как

Пример. Решить задачу методом наискорейшего спуска.

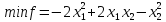
Решение. В качестве исходного приближения берем точку . Вычисляем уклонения точки.

Для нахождения направления спуска ищем частные производные функциив точке: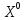

При этом

Решая задачу линейного программирования

получим

Новое приближение:

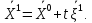
Величина шага

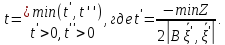
Здесь 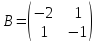и

- наименьшее положительное число среди отношений

Следовательно

.

Отсюда

Вычисляем координаты точки

Определяем уклонения точки .

Для нахождения направления спуска решаем задачу линейного программирования:

Решением будут значения При этом

Новое приближение:

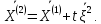
Определим величину шага

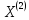Значит, и координаты точкиравны:

Определяем уклонение точки

Для нахождения направления спуска решаем задачу линейного программирования

Решением будут значения Следовательно, является оптимальным решением.

Ответ: