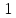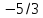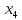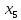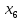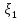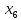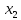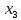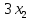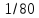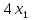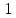2. Если линейная система уравнений обладает планами, то существует равносильная ей каноническая система, которую можно получить из завершающей симплексной таблицы вспомогательной задачи [4].

Таблица «Итерация 2» содержит каноническую систему

Из этой канонической системы при получаем каноническую систему, равносильную исходной ( * ):

(***)

Среди базисных переменных последней симплексной таблицы «Итерация 2» нет ни одной фиктивной переменной.

3. Далее решаем каноническую (или почти каноническую) задачу лп: минимизировать (максимизировать) целевую функцию f основной задачи лп при условиях (***).

Однако может быть случай, когда среди базисных переменных последней симплексной таблицы есть хотя бы одно фиктивное. В этом случае из данной таблицы нельзя сразу выделить каноническую систему. К ней приходят после некоторых преобразований.

4. И, наконец, может быть случай, когда , то есть исходная система планов не имеет и равносильной ей канонической системы не существует [4]. Например:

Исходная таблица

	0	0	0	0	0	1	1
B		Коэффициенты при неизвестных

Итерация 1

B		Коэффициенты при неизвестных

Так как , то исходная система планов не имеет (равносильной ей канонической системы не существует).

§2. Задача о диете

Рассмотрим решение основной задачи ЛП на примере задачи о диете [4].

Для кормления крупного рогатого скота требуется составить суточную диету(рацион), включающую питательные вещества А, В, С (например белки, кальций и т.д.: питательного вещества А не менее 1000 ед., В – не менее 80 ед., С – не менее 300 ед. Эти питательные вещества не могут быть даны в чистом виде, асодержатся в кормах двух видов I и II(например, в концентрата, силосе и т.д.). Известно содержание питательных веществ А, В, С (в ед.) на 1 кг корма каждого вида исебестоимость кормов соответственно 4 и 3 руб.. за 1 кг.Кроме того, суточный рацион должен содержать не более 25 кг корма вида I и 20 кг корма вида II.

Питательные вещества	Содержание (в ед.) в 1 кг корма вида		Минимальная норма питательных веществ (ед.)
	I- концентрат	II- Силос
А (белок)
В (кальций)
С (фосфор)

Определить, сколько килограммов корма каждого вида надо взять для составления суточного рациона, чтобы он был достаточно питательным и имел наименьшую себестоимость.

Обозначим через суточный рацион, в котором – количество корма вида I (в кг); – количество корма видаII.Очевидно,. В рационевещества А будет содержаться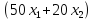ед. Но оно должно входить в рацион в количестве не менее 1000 ед., значит. Аналогичным образом получим еще два неравенства, связанных с минимальной потребностью в питательных веществах В и С:. Кроме того, на один рацион нельзя расходовать больше 25 кг кормаIи 20 кг кормаII, поэтому.

Итак, получим общую задачу ЛП:

В сформулированной задаче – себестоимость рациона.От общей задачи ЛП перейдем к основной, введя добавочные переменные:

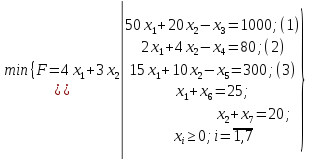(А)

Применив метод искусственного базиса, запишем вспомогательную задачу:

Базис:

Однако можно сократить количество фиктивных переменных, проделав некоторые тождественные преобразования системы(А).Для этого из первого уравнения (1) вычитаем второе (2) и третье (3). Получим систему уравнений, равносильную исходной:

Составим вновь вспомогательную задачу:

Базис: Задача почти каноническая.

Исходная таблица

	0	0	0	0	0	0	0	0	1
B		Коэффициенты при неизвестных
		50

Итерация 1

B

Коэффициенты при неизвестных

10/3

-25/24

1/3

-5/3

-35/48

-1/3

1/48

-1/48

1

10/3

-25/24

Итерация 2

B		Коэффициенты при неизвестных
			1		-5/16				3/10
									-1/10
					-5/4				1/2
				1/40	-1/8				1/10
				-1/80	5/16				-3/10
									-1

Следовательно, линейная система (А) обладает планами. Выпишем каноническую систему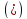, равносильную исходной, из последней симплексной таблицы вспомогательной задачи ЛП:

;

(*)

.

x_i0, I =1,7

Далее решаем почти каноническую задачу: при условиях (*).

Исходная таблица

	0	4	3	0	0	0	0	0
B		Коэффициенты при неизвестных
			1		-5/16
					-5/4
				1/40	-1/8
				-1/80	5/16
				-	-7/16

Получено оптимальное решение (=15, = 25/2, = 0, = 0, = 50, = 10, 15/2),. (см.А).

Вывод:для составления суточного рациона надо взять 15 кг корма видаIи 12.5 кг корма видаII. Рацион будет достаточно питательным, его себестоимость минимальна, а стоимость = 97.5. Значения добавочных переменных () показывают, что питательных веществ видов А и В в рационе содержится соответственно 1000 и 80 ед., а веществ вида С на 50 ед. больше минимальной нормы – 300 ед. Кроме того, для суточного рациона будет израсходовано корма видаIна 10 кг меньше, имеющегося в запасе, а корма видаII– на 7.5 кг меньше.

В заключение отметим, что для некоторых типов задач ЛП (например, для транспортных задач) разработаны дополнительно специальные методы решения, оказывающиеся в ряде случаев более удобными и экономными.

Примечание:Если среди базисных переменных завершающей симплексной таблицы вспомогательной задачи содержится хотя бы одно искусственное переменное, то необходимо провести дополнительные преобразования, прежде чем придем к базису без искусственных переменных [4,c. 44].

Пусть, например, в завершающей симплексной таблице вспомогательной задачи остались ζ₁, ζ₂, Х₁. Выпишем систему, которая при ζ₁ = ζ₂= ζ₃= 0 будет неканонической

Если , то делим 2-е уравнение на, затем исключимиз 1-го и 3-го уравнений (точно также, как в методе Гаусса). Получим

Затем исключим аналогично из 1-го и 2-го уравнения. Придем к канонической системе, равносильной исходной.