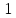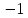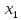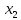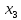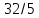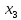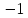- •§1. Этапы решения задачи
- •§2. Некоторые сведения из линейной алгебры.
- •§ 3. Классификация методов математического программирования.
- •§4. Методы исследования функций классического анализа (Аналитические методы)
- •4.1. Необходимые и достаточные условия безусловного экстремума функции
- •4.2. Необходимые и достаточные условия условного экстремума. Принцип Лагранжа.
- •§5. Методы исследования функций численного анализа.
- •Раздел 1.
- •Глава 1. Метод линейного программирования
- •§1. Примеры составления задач лп
- •§ 2. Геометрическая интерпретация решения задачи лп.
- •§ 3. Алгоритм решения канонической задачи лп симплексным методом (метод Данцига).
- •1) Найдется хотя бы одна положительная (отрицательная) оценка и в каждом столбце с такой оценкой найдется хотя бы один положительный элемент, то можно улучшить решение, выполнив следующую итерацию;
- •2) Найдется хотя бы одна положительная (отрицательная) оценка, столбец которой не содержит ни одного положительного элемента, то функция не ограничена в области допустимых решений;
- •§ 4. Решение почти канонических задач.
- •§ 5. Вырожденная задача лп.
- •Глава 2. Решение основной задачи линейного программирования.
- •§1 Сведение основной задачи к двум каноническим.
- •Метод искусственного базиса
- •2. Если линейная система уравнений обладает планами, то существует равносильная ей каноническая система, которую можно получить из завершающей симплексной таблицы вспомогательной задачи [4].
- •3. Далее решаем каноническую (или почти каноническую) задачу лп: минимизировать (максимизировать) целевую функцию f основной задачи лп при условиях (***).
- •§2. Задача о диете
- •Глава 3. Целочисленное линейное программирование.
- •§1 Метод Гомори
- •§2.Пример постановки задачи рационального раскроя [4, c.176].
- •Глава 4. Теория двойственности в лп
- •§ 1. Симметричные двойственные задачи
- •I и II задачи имеют решение.
- •§2. Несимметричные двойственные задачи.
- •Раздел 2. Нелинейное программирование
- •Глава 1.
- •§ 1. Задачи нелинейного программирования с линейной целевой функцией и нелинейной системой ограничений.
- •§ 2. Задачи нелинейного программирования с линейной системой ограничений, но нелинейной целевой функцией.
- •§ 3. Задачи нелинейного программирования с нелинейной системой ограничений и нелинейной целевой функцией.
- •§4. Градиентный метод нелинейного программирования.
- •§5. Выпуклое программирование.
- •Геометрическая интерпретация и графический способ решения задачи квадратичного программирования
- •§6. Параметрическое программирование.
- •Глава 2. Динамическое программирование.
- •Глава 3. Метод случайных испытаний.
- •Глава 4. Геометрическое программирование.
Глава 2. Решение основной задачи линейного программирования.
§1 Сведение основной задачи к двум каноническим.
Метод искусственного базиса
Если основная задача ЛП не является канонической или почти канонической,то симплексным методом можно провести исследование линейной системы основной задачи, что позволит:
Установить наличие или отсутствие планов у данной системы
В случае существования планов построить каноническую систему, равносильную исходной. Две системы с одним и тем же числом неизвестных равносильны (эквивалентны), если каждое решение первой системы является в то же время решением второй системы и наоборот [2].
Рассмотрим пример исследования линейной системы симплексным методом:
 (*)
(*)

Система
неканоническая (нет базиса) . Введем
искусственный базис с помощью так
называемых фиктивных переменных
 ,
, .
Полученная система является канонической:
.
Полученная система является канонической:
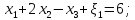 (**)
(**)

Составим так
называемую вспомогательную задачу,
заключающуюся в минимизации целевой
функции
 при условиях (**). Сформулированная
вспомогательная задача ЛП является
почти канонической.
при условиях (**). Сформулированная
вспомогательная задача ЛП является
почти канонической.
1. Для того чтобы линейная система (*) обладала планами, необходимо и достаточно, что бы минимальное значение целевой функции вспомогательной(**)
задачи было
равно нулю
 Если же
Если же
 ,
то линейная система заведомо планов не
имеет [4].
,
то линейная система заведомо планов не
имеет [4].
Решим сформулированную
вспомогательную задачу:
 при условиях (**).В задаче минимизации
нас интересуютположительные оценки.
при условиях (**).В задаче минимизации
нас интересуютположительные оценки.
Исходная таблица
|
|
0 |
0 |
0 |
0 |
1 |
1 |
|
B |
|
Коэффициенты при неизвестных | ||||
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
Итерация 1
|
|
|
|
|
|
|
|
|
B |
|
Коэффициенты при неизвестных | ||||
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
Итерация 2
|
|
|
B |
|
Коэффициенты при неизвестных | ||||
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(32/5;
0; 2/5; 0; 0;)
 .
.
Следовательно, линейная система (*) совместна.