Основное уравнение молекулярно-кинетической теории идеальных газов

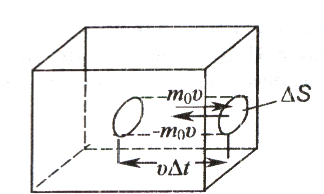
Рассмотрим одноатомный идеальный газ, занимающий некоторый объем. Выделим на стенке сосуда некоторую элементарную площадку ∆S и вычислим давление, оказываемое молекулами газа на эту площадку. Каждая молекула при соударении передает площадке импульс, равный изменению импульса молекулы. За времяплощадкимогут достигнуть только те молекулы, которые заключены в объеме цилиндра с основаниеми высотой. Это число молекул равно.Столкновениями молекул между собой пренебрегаем. Хаотическое движение молекул заменяют движением в трех взаимно перпендикулярных направлениях вдоль осейx,y,z.

Вдоль каждого из них движется 1/3 молекул, 1/6 часть в одном направлении и 1/6 в противоположном. При столкновении с площадкой они передадут ей импульс:

где - число молекул в объеме цилиндра, с основанием ∆S;- изменение импульса одной молекулы

при соударении со стенкой (рис.18).

По второму закону Ньютона,

где F– сила, действующая на стенку площадью ∆S.

Давление газа на стенку .

рис.18

Молекулы газа движутся с различными скоростями v₁,v₂….v_n , поэтому на основании статистического метода необходимо рассматривать среднюю квадратичную скорость движения молекул.

Если , гдеN– общее число молекул,V– объем,

то – кинетическая энергия одной молекулы,m₀– масса молекулы.

,

где Е_К– кинетическая энергия всех молекул.

Это основное уравнение молекулярно-кинетической теории газов (уравнение Клаузиуса). Используя уравнение Клапейрона – Менделеева можно получить выражение для Е₀:

Распределение Максвелла

По молекулярно-кинетической теории, скорости молекул при хаотическом движении изменяются как по модулю, так и по направлению. Однако средняя квадратичная скорость при постоянной температуре остается постоянной, поэтому < Е₀> можно записать как

Постоянство объясняется тем, что в газе устанавливается стационарное, не меняющееся со временем распределение молекул по скоростям. Максвелл вывел функцию распределения молекул по скоростям, имеющую вид:

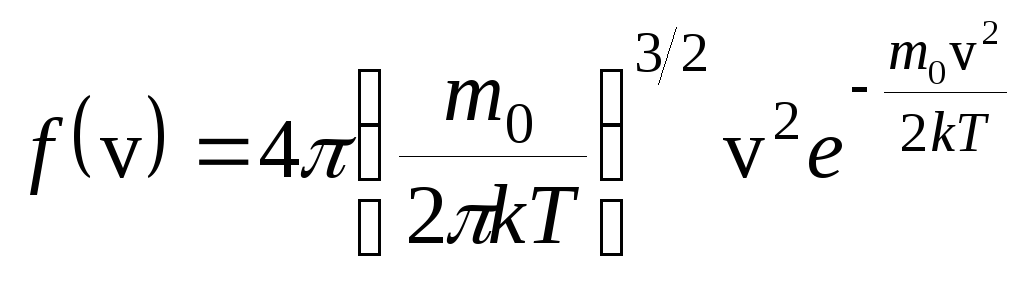
Вид функции зависит от температуры и массы молекул.

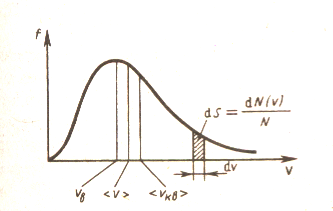
рис.19

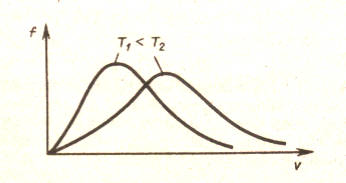
рис.20

Функция прии достигаетпри некотором значенииv_в, а затем стремится к нулю (рис.20). Если разбить диапазон скоростей на малые интервалыdv, тоотносительное число молекул, скорости которых лежат в интервале отvдоравно

откуда

и находится как площадь показанной на рис.19 заштрихованной полоски основанием dvи высотойf(v). Вся площадь, ограниченная кривой, равна 1.

С ростом температуры кривая распределения смещается вправо, т.е. растет число быстрых молекул.

Скорость , которой обладает максимальное число молекул при данной температуре – наиболее вероятная скорость (функцияf(v) достигает максимального значения). Средняя арифметическая скорость рассчитывается как:

Опыт Штерна экспериментально подтвердил справедливость распределения Максвелла.

Среднее число столкновений и средняя длина свободного пробега молекул

Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Путь, который проходит молекула между двумя последовательными столкновениями называется длиной свободного пробега. При большом числе молекул и их столкновений можно говорить о средней длине свободного пробега

( d– диаметр молекулы)

т.е. обратно пропорциональна концентрацииnмолекул. При постоянной температуреnпропорциональна давлениюp. Следовательно

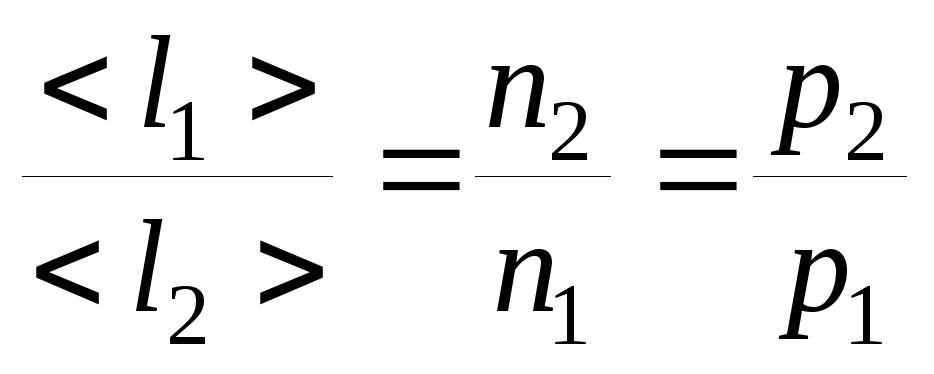
Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром.