
8035
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
числовая |
последовательность |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
, |
|
|
, |
|
, |
, |
|
|
, |
, так |
|
|
как xn |
|
|
– |
формула общего члена |
|||||||||||||
|
|
|
|
|
n |
n 1 |
||||||||||||||||||||||||||
2 3 4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
последовательности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
При n 1: x |
|
|
|
|
1 |
|
|
|
1 |
. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 1 |
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
При n 2 : |
x |
|
|
1 |
|
|
|
|
|
1 |
. |
|
|
|
|
|||||||||||||
|
|
|
|
2 |
2 1 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
При |
n 3: x |
|
|
|
1 |
|
|
|
|
1 |
и т.д. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 1 |
4 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пределом числовой последовательности xn называется конечное действительное число a , если для любого сколь угодно малого числа
0 существует |
такое |
натуральное |
число |
N , что для всех членов |
||||||||||||||
последовательности |
с |
номерами |
n N |
выполняется неравенство |
||||||||||||||
|
xn a |
|
. В краткой записи это выглядит так: |
|
||||||||||||||
|
|
|
||||||||||||||||
|
|
|
0 N n N |
|
xn a |
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||||
и обозначается: lim xn a . |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим |
– |
окрестность точки |
a |
как множество |
всех x , |
|||||||||||||
удовлетворяющих |
условию: |
|
x a |
|
, |
что эквивалентно |
двойному |
|||||||||||
|
|
|||||||||||||||||
неравенству: a x a .
Тогда понятие предела геометрически означает, что какую бы малую– окрестность точки a не взяли, найдется такой номер N , начиная с которого все последующие члены последовательности будут находиться в этой окрестности (См. рис. 52).
21

x1 |
xN 1 |
xN 2 xn |
x2 |
a |
a |
|
a |
|
|
Рис. 52 |
|
Последовательность, имеющая конечный предел, называется сходящейся или стремящейся к этому пределу, а неимеющая конечного предела – расходящейся. «Стремление» последовательности xn к своему
пределу a будем обозначать как xn a . |
|
|
|
|
||||||||||||||||||
|
|
|
|
Пример. Доказать по определению, что lim |
1 |
0 . |
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n n |
|
|
|
|
|
|
|
|
|
Решение. |
Возьмем любое |
|
сколь угодно |
малое |
0 . |
Имеем: |
||||||||||||
|
|
1 |
0 |
|
, когда |
1 |
или |
n |
|
1 |
. Значит существует такой номер |
N , |
||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||||
равный целой |
части |
числа |
1 |
, |
|
то есть такое |
целое |
число |
N , |
что |
||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
1 |
N 1, |
то есть |
N |
1 |
|
, |
начиная с которого все последующие |
|||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
члены с номерами |
N , N 1, |
|
N 2, N 3, ... будут находиться в – |
|||||||||
окрестности точки |
x 0, то есть в интервале ; . (См. рис.53). При |
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
0,2 |
N |
|
5, при |
0,01 |
N |
|
100 . |
|||||
|
|
|||||||||||
|
|
0,2 |
|
|
|
|
|
|
|
|
0,01 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
N 2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
N 3 |
N 1 |
|
|
||||
|
|
|
0 |
|
|
Рис. 53 |
|
|
||||
|
|
|
|
|
|
|
|
|||||
Замечание. |
|
|
|
|
|
|
|
|
|
|
||
lim xn означает, что 0 |
N , |
n N xn ; |
||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
lim xn означает, что 0 |
N , n N xn . |
n |
|
При вычислении пределов числовой последовательности полезно использовать следующие их свойства, если существуют конечные пределы
lim xn a |
и lim yn b , то |
n |
n |
1) |
lim c c , c const ; |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
lim |
c xn c lim xn |
c a , |
c const ; |
|
|
|
|
|
||||||||||||||
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||
3) |
lim |
xn |
yn lim xn |
lim yn |
a b; |
|
|
|
|
|
|||||||||||||
|
n |
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|||
4) |
lim |
xn |
yn lim xn lim yn |
a b ; |
|
|
|
|
|
|
|||||||||||||
|
n |
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
||||
|
|
|
x |
n |
|
lim xn |
|
a |
, если b 0; |
|
|
|
|
|
|
||||||||
5) |
lim |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
y |
|
|
lim y |
|
b |
|
|
|
|
|
|
|||||||||||
|
n |
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6) |
lim |
1 |
|
0, если lim x a . |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
n x |
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть |
|
|
|
требуется |
|
найти |
предел |
lim |
xn |
отношения |
двух |
||||||||||||
|
|
|
|
y |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
последовательностей, сходящихся к бесконечности, |
то есть |
lim xn |
и |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
lim yn .
n
Непосредственно применить свойство о пределе частного двух последовательностей нельзя. Предварительно необходимо преобразовать
выражение |
xn |
к виду, допускающему применение указанных свойств. В |
||||
yn |
||||||
|
|
|
|
|
||
связи с этим |
выражение |
|
|
называется неопределенностью, а его |
||
|
|
|||||
|
|
|
|
|
|
|
преобразование к виду, позволяющему найти предел – раскрытие неопределенности.
23

0
Заметим, что выражение , когда последовательности в числителе
0
и знаменателе стремятся к нулю, также называются неопределенностью.
Пример. |
|
Вычислить lim |
n2 2n 3 |
. |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
n |
3 |
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Разделим числитель и знаменатель на n3 |
– наибольшую из |
||||||||||||||||||||||||||||||||||||||||||
степеней n в числителе и знаменателе: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
n2 |
|
|
|
2n |
|
|
3 |
|
|
|
1 |
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
lim |
|
n3 |
|
|
n3 |
|
|
|
n3 |
|
|
lim |
n |
|
|
n2 |
|
|
|
|
n3 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
3 |
|
1 |
|
|
1 1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
n |
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
n3 |
|
|
n3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
lim |
1 |
2 lim |
1 |
|
|
3lim |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 2 0 3 0 |
|
0 |
|
|
||||||||||||||||||||||||||
|
n n |
|
|
|
n n2 |
|
|
n n3 |
|
|
|
|
0 . |
||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
1 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n n3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Предел функции.
Пределом функции y f x в точке |
x x0 называется такое число |
||
A, что для |
любой последовательности |
xn значений |
аргумента x , |
сходящейся |
к числу x0 , последовательность yn , |
yn f xn |
|
соответствующих значений функции y стремится к этому числу A и
обозначается: lim f x A.
x x0
При нахождении пределов функций нужно использовать следующие
свойства предела функции: если существуют конечные пределы lim f x
x a
и lim g x , то |
|
|
||
x a |
|
|
|
|
1) |
lim c f x c lim f x , c const ; |
|||
|
x a |
|
x a |
|
2) |
lim |
f |
x g x lim |
f x lim g x ; |
|
x a |
|
x a |
x a |
3) |
lim |
f |
x g x lim |
f x lim g x ; |
|
x a |
|
x a |
x a |
|
|
|
|
24 |
4) lim |
1 |
|
0 (или ), если lim |
f x (или 0); |
||||||||
|
|
|||||||||||
f x |
||||||||||||
x a |
|
|
f x |
|
|
x a |
|
|||||
|
f x |
|
lim |
, если lim g x 0 . |
||||||||
5) lim |
x a |
|
|
|||||||||
|
|
|
|
|
||||||||
g x |
|
lim g x |
||||||||||
x a |
|
|
|
x a |
|
|||||||
|
|
|
|
x a |
|
|
|
|
|
|
|
|
Пример. Вычислить lim |
x2 |
1 |
. |
|
||||||||
|
x |
|
||||||||||
|
|
|
|
|
n 3x2 |
|
|
|||||
Решение: Разделим числитель и знаменатель на x2 , получим:
|
|
|
|
|
|
|
|
x2 |
1 |
|
|
|
1 |
|
|
|
|||||||
|
x2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
lim |
|
lim |
|
|
x2 |
x2 |
|
lim |
x2 |
|
|
||||||||||||
3x x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
3x |
2 |
|
|
x |
|
|
1 |
|
|
|
|||||||||
n |
2 |
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||||
|
|
|
|
|
|
|
|
x2 |
x2 |
|
|
|
|
||||||||||
|
lim 1 lim |
1 |
|
|
|
|
|
|
|
|
||
x2 |
|
|
1 0 |
|
|
1 |
|
|||||
|
x |
x |
|
|
|
|
. |
|||||
|
|
|
|
3 0 |
|
|||||||
|
lim 3 lim |
1 |
|
|
|
|
3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
x x |
|
|
|
|
|
|
|
|||
При нахождении пределов функций также полезно знать первый
замечательный предел: lim |
sin x |
|
1 и следствия из него: |
|
|
|
|||||||||||||||||||||||||||
|
|
x |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
lim |
tg x |
1; |
|
lim |
|
arcsin x |
|
1; |
|
|
lim |
|
arctg x |
1; |
||||||||||||||||
|
|
|
x |
|
|
|
|
x |
|
|
|
|
x |
||||||||||||||||||||
|
|
|
x 0 |
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
и второй замечательный предел: |
lim 1 |
|
|
lim 1 x |
|
e . |
|||||||||||||||||||||||||||
|
x |
||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
x |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример. Вычислить предел |
lim |
|
|
sin 2x |
. |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
arctg 3x |
|
|
|
|
|
||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
sin 2x |
|
|
0 |
|
|
2 |
lim |
sin 2x |
|
|
3x |
|
|
|
|
|
|
|||||||||||||||
arctg 3x |
0 |
|
|
|
|
arctg3x |
|
|
|
||||||||||||||||||||||||
x 0 |
|
|
3 |
|
x 0 |
2x |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
lim |
sin 2x |
lim |
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
3 x 0 |
2x |
|
x 0 |
arctg3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
25

|
|
t 2x |
|
|
2 |
lim |
sin t |
lim |
y |
|
2 |
1 1 |
2 |
. |
|
|
|||||||||||||
|
y 3x |
|
|
|
|
|
|
|||||||
|
|
|
|
3 t 0 |
t |
y 0 |
arctgy |
|
3 |
|
3 |
|
||
2
Пример. Вычислить предел lim 1 3x x .
x 0
Решение.
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 lim |
|
1 |
|
|
3 x |
|
|
lim 3 x |
2 |
|
|
|
1 |
|
||||||||
2 |
1 |
x |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
lim 1 3x |
|
|
3x |
|
|
|
ex 0 |
x |
e 6 |
|
|
|
|
. |
|||||||||
x |
3 x |
|
|
|
|
||||||||||||||||||
|
|
e |
|
||||||||||||||||||||
x 0 |
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Общий метод (правило Лопиталя) вычисления пределов в случаях |
|||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неопределенности |
|
|
и |
|
|
рассматривается |
в дифференциальном |
||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
исчислении. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть y f x функция от x , имеющая пределом число |
A, когда |
||||||||||||||||||||||
x стремится к числу a . |
Предположим, |
что все значения величины x |
|||||||||||||||||||||
меньше, чем число a , |
то есть x a . Символически это выражается очень |
||||||||||||||||||||||
удобной записью: |
|
x a 0 |
(вместо |
x a, x a). |
|
|
Тогда |
|
предел |
||||||||||||||
lim f x A1 называют пределом функции |
f x в точке x a слева или |
||||||||||||||||||||||
x a 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
левосторонним пределом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Аналогично, |
при |
x a, x a , |
то |
есть |
x a 0 |
|
предел |
||||||||||||||||
lim f x A2 называют пределом функции |
f x |
в точке |
x a справа |
||||||||||||||||||||
x a 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или правосторонним пределом.
Левосторонний и правосторонний пределы функции в точке называются односторонними пределами.
Дадим определение непрерывности функции в точке.
Функция y f x называется непрерывной в точке x x0 , если:
1) функция f x определена в точке x0 и в некоторой ее окрестности, содержащей эту точку x0 ;
26
2) |
функция |
f x имеет одинаковые односторонние пределы в этой |
|||
точке x0 |
, то есть |
lim |
f x lim |
f x ; |
|
|
|
x x0 0 |
x x0 0 |
|
|
3) |
эти односторонние пределы должны быть равны значению |
||||
функции f x в этой точке x0 : lim |
f x f x0 . |
|
|||
|
|
|
x x0 |
|
|
Функция y f x называется разрывной в точке |
x x0 , если она |
||||
определена в сколь угодно малой окрестности точки x0 , |
но в самой точке |
||||
x0 не удовлетворяет хотя бы одному из условий непрерывности.
Точки разрыва функции можно разделить на два типа.
Точка разрыва x0 функции y f x называется точкой разрыва 1-
го рода, если существуют конечные односторонние пределы функции в этой точке, которые не равны между собой или равны между собой, но не равны значению функции в этой точке. Если хотя бы один из односторонних пределов функции в точке x0 не существует или равен бесконечности, то x0 – точка разрыва функции 2-го рода.
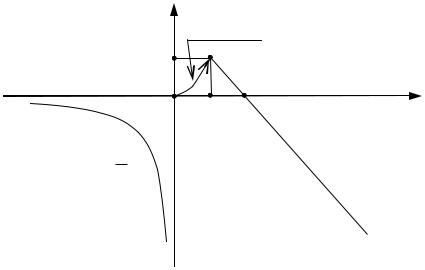
Пример. Исследовать на непрерывность функцию и построить ее
|
|
1 |
, при x 0 |
|
|
|
|
|
x |
||
|
|
||
|
|
|
|
график y x2 , при 0 x 1. |
|||
|
2 x, при x 1 |
||
|
|
|
|
|
|
|
|
Решение. |
Областью определения данной функции y является вся |
|||||
числовая ось, |
то |
есть |
D R . |
Точками «подозрительными» на точки |
||
разрыва являются точки |
x1 |
0 |
и |
x2 1, так как при переходе через эти |
||
точки функция |
y |
меняет |
свое |
аналитическое выражение с дробно – |
||
рациональной на квадратичную и с квадратичной на линейную, соответственно.
Исследуем непрерывность функции y в точке x1 0 :
27

lim |
y lim |
1 |
|
1 |
|
|
x |
0 |
|||||
x 0 0 |
x 0 |
|
|
lim y lim x2 0 2 0
x 0 0 x 0
y 0 x2 x 0 02 0
Поскольку условие непрерывности функции y в точке x1 0
нарушается, то x1 0 – точка разрыва функции y , т.к. левосторонний предел функции y в точке x1 0 равен бесконечности, то x1 0 – точка
разрыва 2-го рода.
Исследуем непрерывность функции y в точке x2 1:
lim y lim x2 |
1 0 2 |
1 |
|
x 1 0 |
x 1 0 |
|
|
lim y lim x2 |
2 x 2 |
2 1 0 1 |
|
x 1 0 |
x 1 0 |
|
|
y 1 2 x x 1 2 1 1
Условие непрерывности функции y в точке x2 1 выполняется,
значит, функция y в точке x2 1 непрерывна.
Построим график функции y :
28
|
y |
y x2 |
|
|
1 |
|
|
|
0 |
1 2 |
x |
y |
1 |
|
y 2 x |
|
x |
|
|
Рис. 54
Производная
Пусть функция y f x определена на некотором интервале a;b .
Аргументу |
x a;b |
дадим |
|
приращение |
x , |
получим |
точку |
||||||||||||
x x a;b . |
Найдем |
соответствующее |
приращение |
функции: |
|||||||||||||||
y f x x f x . |
Составим отношение приращения |
y |
функции |
||||||||||||||||
y к приращению x аргумента |
x : |
y |
и найдем предел этого отношения |
||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
при x 0, |
то |
есть |
lim |
y |
. Если |
этот |
предел |
существует, |
то |
его |
|||||||||
|
|
|
|
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
называют |
производной |
функцией |
от |
данной функции |
y f x |
и |
|||||||||||||
обозначают одним из символов: |
|
|
|
dy |
, |
f |
|
, |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||||||
y x , |
dx |
x |
yx . |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, по определению |
|
|
y x x y x |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
y |
x lim |
|
|
x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Функция |
y f x , |
имеющая |
производную |
в каждой |
точке |
||||||||||||||
интервала |
a;b , |
называется дифференцируемой в |
этом |
интервале, а |
|||||||||||||||
|
|
|
|
|
|
|
|
29 |
|
|
|
|
|
|
|
|
|
|
|

операция |
нахождения |
производной |
функции |
называется |
|||
дифференцированием. |
|
|
y f x |
|
|
|
|
Значения производной |
функции |
|
|
в |
точке x x0 |
||
обозначается одним из символов: y x0 , |
f x0 или y |
|
x x0 . |
|
|||
|
|
||||||
Пример. Найти по определению производную функции y x2 . Решение. Областью определения D данной функции является вся
числовая ось, то есть D R . Выберем произвольную точку x R . Дадим
ей приращение x , получим новую |
точку x x R . Находим |
соответствующее приращение y функции |
y x2 : |
y y x x y x x x 2 x2
x2 2x x x 2 x2 2x x x 2 .
Составим отношение |
y |
|
2x x x 2 |
2x x |
и найдем предел |
|
x |
x |
|||||
|
|
|
|
|||
отношения при x 0: |
|
|
|
|
||
lim |
y lim 2x x 2x 0 2x . |
|
||||
x 0 |
x |
x 0 |
|
|
||
Поскольку данный предел существует, то производная функции y x2 в
точке x равна 2x , то есть x2 2x .
Пусть материальная точка (тело) движется неравномерно по закону прямолинейного движения S S t . Каждому значению истекшего времени t соответствует определенное расстояние S до некоторой фиксированной точки O . Тогда средняя скорость Vcp движения точки за
время t равна:
Vcp St , где S S t t S t .
Предел средней скорости Vcp движения при стремлении к нулю
промежутка времени t называется скоростью V движения точки в данный момент времени (или мгновенной скоростью)
V lim S .
t 0 t
30
