
6856
.pdf
|
|
|
|
|
70 |
|
|
уравнениями Лагранжа II-го рода: |
|
|
|||||
qŒˆ " qŒ |
|
|
, Š 1,2, … , ? |
|
|
||
qh |
qh |
|
‰ |
|
. |
(13.6) |
|
• |
|
• |
|
|
|
||
|
|
|
|
|
|||
¸ ¸ ¹ , … , ¹ , ¹ˆ, … , ¹ˆ |
|
|
|
|
|
|
|
После подстановки в них выражения кинетической энергии |
|
||||||
|
они приобретают вид обыкновенных дифференци- |
||||||
альныхH уравненийº » ºII-го рода»I |
, в которых неизвестными являются обобщенные |
||||||
координаты.
13.3. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА ДЛЯ КОНСЕРВАТИВНЫХ МЕХАНИЧЕСКИХ СИСТЕМ
Если все действующие на механическую систему силы являются потенциальными, то обобщенные силы определяются формулой
‰П " qŒq¼• , |
Š 1,2, … , ?. |
|
||||
Тогда уравнение Лагранжа II-го рода принимает вид |
||||||
qŒˆ " qŒ |
" qΠ|
, |
Š 1,2, … , ? |
|
||
qh• |
qh• |
|
q¼• |
|
|
. |
Если учесть, что потенциальная энергия системы не зависит от скоростей, то |
||||||||
естьqŒq¼• 0,то полученные уравнения можно переписать так: |
|
|||||||
|
qŒˆ |
" |
qΠ|
|
0, Š 1,2, … , ? |
|
|
|
qHТ¾ПI |
|
qHh¾ПI |
|
|
. |
|
||
|
• |
|
|
• |
|
|
|
|
Ведем обозначение |
|
|
|
|
|
|
|
|
• ^ " ¿, |
|
|
|
|
|
(13.7) |
||
И вновь запишем уравнения: |
|
Š 1,2, … , ? |
|
|
|
|||
qŒˆ " qŒ |
0, |
|
|
|
||||
|
q˥ |
q˥ |
|
|
|
. |
|
(13.8) |
Эти уравнения называются уравнениями Лагранжа второго рода для консервативных систем.
Функция L = T − Π называется функцией Лагранжа или кинетическим потенциалом.

71
Тема 14. Удар
14.1. УДАРНЫЙ ИМПУЛЬС
Явление, при котором скорости точек тела за малый промежуток времени ме-
няются на |
конечную |
величину, называется ударом. |
||||||
Ударный импульс |
|
удср |
|
|
||||
|
|
|
|
Á |
|
|||
& |
уд = |
|
удdt = |
|
|
(14.1) |
||
|
|
|
|
|
|
|||
отличается от импульса неударных сил тем, что время удара τ мало, ударные силы Fуд велики, а Sуд принимает конечное значение. Поэтому, изучая удар, будем пренебрегать:
неударными силами по сравнению с ударными, перемещениями точек тела во время удара.
Теорема об изменении количества движения в случае удара имеет вид: |
||||||
|
" |
|
$ |
. |
|
|
|
|
∑ & |
% |
(14.2) |
||
|
|
|
|
|
||
А теорема об изменении кинетического момента системы относительно неко-
торой точкиА имеет вид:
-Ä = ∑$ Å C $D.
Тогда, для случая удара, с учетом (14.1) получим: |
|
|||||
Å |
Å |
Å $ |
|
|||
: |
- |
: |
= |
∑ & |
% |
(14.3) |
|
|
|
||||
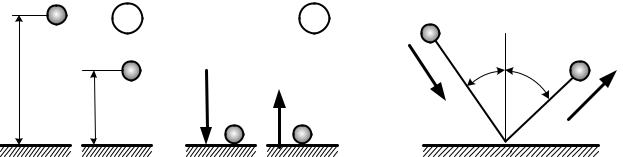
14.2. УДАР МАТЕРИАЛЬНОЙ ТОЧКИ О ПОВЕРХНОСТЬ |
|
|
||
Пусть точка массой mс некоторой высоты Н падает на поверхность и отскаки- |
, |
|||
|
Скорость точки при ударе о поверхность равна |
ѵ |
||
вает на высотуh(рис. 14.1, а). |
u (рис. 14.1, б). Очевидно, что u<ѵ. |
|
||
а при отскоке от поверхности |
|
|
||
Отношение k = |
Çѵназывают коэффициентом восстановления при ударе. |
|
|
|
Его можно найти экспериментально. |
|
|
||
Согласно формуле Галилея, ѵ = |
;2WÈ, u = ;2W), |
|
|
|
откуда |
k = ;)/È. |
(14.4) |
|
|
72
Коэффициент восстановления меняется в пределах 0 ≤ k ≤ 1.
Теорема об изменении количества движения в случае удара материальной точки массой m о поверхность запишется следующим образом
mu - mv = Sуд |
(14.5) |
H |
R |
α |
β |
v |
R |
|
|
|
|
u |
R |
|
|
|
|
|
h |
R |
u |
|
v |
|
Рис. 13.1 |
Рис. 13.2 |
14.3. КОСОЙ УДАР
ПРИМЕР
Материальная точка падает со скоростью ѵ на гладкую плоскость под угломα. Под каким углом β (рис. 14.2) отскочит точка от поверхности, если коэффициент восстановления равен k?
Решение
Запишем закон изменения количества движения точки в проекции на плоскость (ось х). Так как плоскость гладкая, горизонтальных сил и их импульсов нет. Закон изменения имеет форму закона сохранения:
mux - mѵx = 0 |
(14.6) |
Так какux= u?Ê> Ë, ѵx = ѵ ?Ê> U , то |
u?Ê> Ë=ѵ ?Ê> U. |
Модули нормальных проекций скоростей связаны коэффициентом восстановления:
k = |
Ç –—‡ Ì |
(14.7) |
|
ѵ –—‡ Í |
|||
|
|
Из (14.6) и (14.7) следует, что tgβ = (1/k) tgU.При k = 0 получим, что β = π/2, то есть точка покатится по поверхности (мяч, брошенный в песок).
73
ЛИТЕРАТУРА
1.Диевский, В.А. Теоретическая механика: Учебное пособие. 2-е изд., испр.
– СПб.: Издательство «Лань», 2008. – 320 с.
2.Лойцянский, Л.Г. Курс теоретической механики /Л.Г.Лойцянский,
А.И.Лурье.В 2 т. Т.2 Динамика. – М.: ГИТТЛ, 1955. – 595 с.
3.Мещерский, И.В. Сборник задач по теоретической механике: Учебное пособие / И.В. Мещерский. −М.: Наука, 1986. − 448 с.
4.Сб. заданий для курсовых работ по теоретической механике: Учебное по-
собие / Под ред. А.А.Яблонского. − М. Высш. школа, 1985 − 367 с.
5.Аистов А.С. Теоретическая механика. Динамика. Учебное пособие /
А.С.Аистов, А.С.Баранова, Н.Ю. Трянина.- Н.Новгород: Нижегородский государственный архитектурно-строительный университет.
6. Куликов, И.С. Сборник задач по теоретической механике: Учебное пособие / И.С. Куликов, Н.Ю. Трянина. – Н. Новгород: Изд-во ННГАСУ, 2002. – 84с.

Самостоятельная работа по АНАЛИТИЧЕСКОЙ МЕХАНИКЕ
Учебно-методическое пособие
по подготовке к лекционным и практическим занятиям по дисциплине «Аналитическая механика»
для обучающихся по направлению подготовки 08.03.01 Строительство Профиль Промышленное и гражданское строительство.
Федеральное государственное бюджетное образовательное учреждение высшего образования «Нижегородский государственный архитектурно-строительный университет»
603950, Нижний Новгород, ул. Ильинская, 65.
http://www. nngasu.ru, srec@nngasu.ru
