
6762
.pdf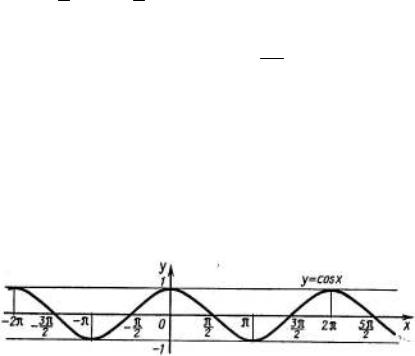
70
Ответы. 1.1. чётная ;1.2. нечётная; 1.3. нечётная; 1.4. нечётная; 1.5. чётная; 1.6. чётная. 2.1. нечётная; 2.2. общего вида; 2.3. чётная; 2.4. чётная; 2.5.
общего вида; 2.6. − 5 ≤ y ≤ − 3. 5.1. чётная; 5.2. чётная; 5.3. нечётная; 5.4.
44
нечётная; 5.5. чётная; 5.6. чётная. 6.1. 5π ; 6.2. 4π ; 6.3. 2π ; 6.4. π . 3
7.3. Функция y = cos x, её свойства и график
Основные свойства функции y = cos x (рисунок 7.1)
Рисунок 7.1. График функции y = cos x
1.Область определения – множество R всех действительных чисел.
2.Множество значений – отрезок [−1; 1].
3.Функция y = cos xпериодическая с периодом 2π .
4.Функция y = cos xчётная.
5.Функция y = cos xпринимает
- значение равное 0 при x = π + πn , n Z; 2
-наибольшее значение, равное 1, при x = 2πn , n Z;
-наименьшее значение, равное -1, при x = π + 2πn , n Z;
|
− |
π |
+ 2πn; |
π |
+ |
|
|
||
- положительные значения на интервалах |
|
|
|
2πn , n Z; |
|||||
|
|
2 |
|
|
2 |
|
|
|
|
π |
|
|
3π |
|
|
|
|
|
|
- отрицательные значения на интервалах |
|
+ |
2πn; |
|
|
+ 2πn , |
n Z. |
||
|
|
|
|||||||
2 |
|
|
2 |
|
|
|
|
|
|

71
6. Функция y = cos x
- возрастает на отрезках [π + 2πn; 2π + 2πn], n Z; - убывает на отрезках [2πn; π + 2πn], n Z.
Задача 1. Найти все корни уравнения cos x = − 1 , принадлежащее отрезку
2 |
|
|
−π ≤ x ≤ 2π . |
|
|
Решение. На отрезке [− π ; 2π ] графики y = cos x и y = − |
1 |
(рисунок 7.1) |
|
||
2 |
|
|
пересекаются в трёх точках с абсциссами − 2π , 2π , 4π . Это и есть корни
|
|
|
|
|
3 |
3 |
3 |
|
исходного уравнения. |
|
|
|
|
|
|
|
|
|
2π |
|
2π |
|
4π |
|
|
|
Ответ. x − |
|
, |
|
, |
|
. |
|
|
|
|
|
|
|
||||
|
3 |
|
3 |
|
3 |
|
|
|
Задача 2. Найти все решения неравенства |
cos x > − |
1 |
, принадлежащие |
|||||||||
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
||
отрезку −π ≤ x ≤ 2π . |
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Из рисунка 7.1 видно, что график функции |
y = cos x лежит |
|||||||||||
|
1 |
|
|
2π |
|
2π |
|
4π |
|
|||
выше графика функции y = − |
|
на промежутках − |
|
|
; |
|
и |
|
|
; 2π . |
||
|
2 |
|
3 |
|
3 |
|
3 |
|
||||
|
|
2π |
|
2π |
|
4π |
|
|
Ответ. x |
− |
|
; |
|
|
|
|
; 2π . |
|
|
|
||||||
|
|
3 |
|
3 |
|
3 |
|
|
Упражнения
1. Сравнить числа, используя свойство возрастания и убывания функции
y = cos x
1.1. cosπ и cos |
8π |
; |
1.2. cos |
8π |
и cos |
10π |
; |
|
|
|
|||||
7 |
9 |
|
7 |
7 |
|
||
|
|
|
|
|
|
|
|
72 |
|
|
|
|
|
|
|
|
|
|
− |
6π |
|
− |
π |
|
|
− |
8π |
|
− |
9π |
|||
1.3. |
cos |
|
и |
cos |
; |
1.4. |
cos |
|
и |
cos |
|
; |
||||
|
|
|
||||||||||||||
|
|
|
7 |
|
|
8 |
|
|
|
7 |
|
|
7 |
|||
1.5. cos1и cos3; |
|
|
|
1.6. cos4и cos5. |
|
|
|
|||||||||
2. Найти все корни уравнения, принадлежащие отрезку [0; 3π ]
2.1. cos x = |
1 |
; |
|
|
|
1.2. cosx = |
2 |
|
; |
||
|
|||||||||||
|
|
|
|
||||||||
2 |
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
1 |
|
|||
2.3. cosx = − |
|
2 |
; |
1.4. cos x = − |
. |
||||||
|
|
|
|
|
|||||||
|
|||||||||||
|
|
2 |
|
|
2 |
|
|
||||
3. Найти все корни неравенства, принадлежащие отрезку [0; 3π ]
3.1. cos x ≥ |
1 |
; |
|
|
3.2. cos x ≥ − |
1 |
; |
||||
|
|
||||||||||
2 |
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
3.3. cosx < − |
|
2 |
; |
3.4. cosx < |
3 |
. |
|||||
|
|
||||||||||
|
|
2 |
|
2 |
|
|
|||||
4. Сравнить числа, выражая синус через косинус по формулам приведения 2.7
4.1. cosπ и sin π ; |
4.2. sin π и cosπ ; |
||||||||||||
5 |
5 |
|
|
7 |
7 |
|
|
||||||
4.3. cos |
5π |
и sin |
5π |
; |
4.4. sin |
3π |
и cos |
3π |
; |
||||
|
|
|
|
|
|
||||||||
8 |
8 |
|
5 |
5 |
|
||||||||
4.5. cosπ и sin |
5π |
; |
4.6. cosπ и sin |
3π |
. |
||||||||
|
|
||||||||||||
6 |
14 |
|
|
8 |
10 |
|
|
||||||
5. Найти все корни уравнения, принадлежащие промежутку − π ≤ x ≤ 3π 2 2
5.1. cos2x = |
1 |
; |
5.2. cos3x = |
3 |
. |
|
|
||||
2 |
|
2 |
|
||

73
6. Найти все решения неравенства, принадлежащие промежутку
|
|
− π ≤ x ≤ |
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
6.1. cos2x < |
1 |
; |
|
|
|
6.2. cos3x > |
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
7. Построить график функции и выяснить её свойства |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
7.1. y = 1+ cos x ; |
|
|
|
7.2. y = cos x − 2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
7.3. y = cos 2x ; |
|
|
|
|
7.4. y = 3cos x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
8. Найти множество значений функции |
|
y = cosx, если x принадлежит |
||||||||||||||||||||||||||||||||||||||||||||
|
|
промежутку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5π |
|
|
7π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
8.1. |
|
; π |
; |
|
|
|
|
|
|
|
|
8.2. |
|
|
|
; |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
9. Построить график функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
9.1. y = |
|
cosx |
|
; |
|
|
|
|
9.2. |
y = 3 − 2cos(x −1). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Ответы. |
|
|
|
|
|
1.1.cos π > cos |
8π |
; |
|
|
|
|
|
|
1.2.cos |
8π |
< cos |
10π |
; |
|
|
|
1.3. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
7 |
|
|
|
|
|
|
|||
|
|
|
6π |
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
8π |
|
|
|
|
|
|
|
9π |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
cos |
− |
|
|
|
< cos − |
|
|
|
|
; |
1.4. |
cos |
− |
|
|
|
< cos |
− |
|
|
|
; |
1.5. |
cos1> cos3; |
1.6. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
7 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
cos4 < cos5. |
|
|
2.1.x = π ; |
5π |
; |
7π |
.; |
2.2.x = π ; |
7π |
; |
9π |
; |
2.3. |
x = |
3π |
; |
5π |
; |
11π |
; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
3 |
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
4 |
|
|
|
4 |
4 |
|
4 |
|
||||||||
2.4.x = |
2π |
; |
4π |
; |
7π |
. 3.1. |
0 ≤ x ≤ π ; |
5π |
≤ x ≤ |
7π |
; 3.2. |
0 ≤ x ≤ |
2π |
; |
4π |
≤ x ≤ |
7π |
; |
|
|
|
|
|
|
|
|
|||||||||||
3 |
3 |
3 |
|
3 |
3 |
3 |
|
3 |
3 |
3 |
|
|||||||
3.3.π < x < 11π ; 13π < x ≤ 3π ; 3.4. 3π < x < 5π ; 11π < x < 3π ; 4.1.cos π > cos 3π
6 |
6 |
6 |
|
|
4 |
4 |
4 |
|
|
|
5 |
10 |
4.2. sin π < cos π ; |
4.3. |
cos |
5π |
> cos π ; 4.4. |
sin |
3π |
> cos |
3π |
; 4.5. |
cos π < cos π ; |
||
|
|
|
||||||||||
7 |
7 |
|
8 |
8 |
|
5 |
5 |
|
6 |
7 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4.6. cos π > sin |
3π |
. 5.1. x = π ; |
; |
5π |
; |
|
7π |
; |
5.2. x = − |
π |
; |
π |
; |
|
11π |
; |
13π |
; |
|
23π |
; |
|
25π |
. |
|||||||||||||||||||||||||||
|
8 |
|
|
|
10 |
|
|
|
6 |
6 |
|
6 |
|
|
|
|
12 |
12 |
12 |
|
|
12 |
|
|
12 |
12 |
|
|
|||||||||||||||||||||||
6.1.π < x < |
5π |
; |
|
|
7π |
< x < |
3π |
; 6.2.− |
π |
< x < |
π |
; |
|
11π |
< x < |
13π |
; |
|
23π |
< x < |
25π |
. |
|||||||||||||||||||||||||||||
6 |
6 |
|
|
6 |
|
|
2 |
|
|
|
|
|
12 |
|
|
12 |
|
12 |
|
|
|
12 |
|
|
12 |
|
|
12 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
8.1. −1≤ y ≤ − |
|
|
3 |
; 8.2. − |
|
|
2 |
< y < |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
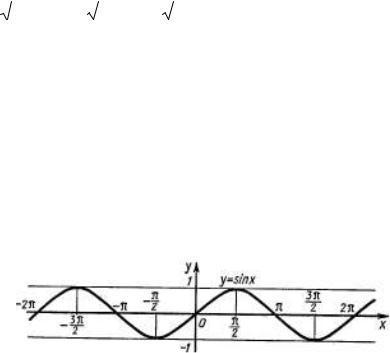
7.4. Функция y = sin x , её свойства и график
Основные свойства функции y = sin x (рисунок 7.2)
Рисунок 7.2. График функции y = sin x
1.Область определения – множество R всех действительных чисел.
2.Множество значений – отрезок [−1; 1].
3.Функция y = sin x периодическая с периодом 2π .
4.Функция y = sin x – нечётная.
5.Функция y = sin x принимает
-значение, равное 0, при x = πn , n Z;
-наибольшее значение, равное 1, при x = π + 2πn , n Z;
2
- наименьшее значение, равное -1, при x = − π + 2πn , n Z; 2
-положительные значения на интервалах (2πn; π + 2πn), n Z;
-отрицательные значения на интервалах (π + 2πn; 2π + 2πn), n Z.
|
|
|
|
|
75 |
|
|
|
|
|
|
|
6. Функция y = sin x |
|
|
|
|
|
|
|
|
|
|
|
|
- возрастает на отрезках |
|
π |
+ 2πn; |
π |
|
|
, n |
Z; |
||||
− |
|
|
+ 2πn |
|||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
π |
|
|
|
|
3π |
|
|
|
|
|
|
- убывает на отрезках |
|
+ 2πn; |
|
|
+ 2πn |
, n Z. |
|
|||||
|
|
|
||||||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
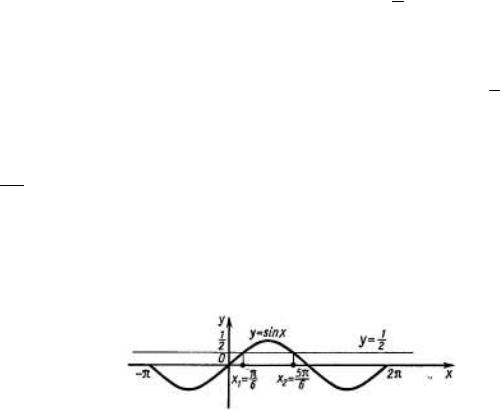
Задача 1. Найти все корни уравнения sin x = 1 , принадлежащее отрезку 2
−π ≤ x ≤ 2π .
Решение. Построим графики функций y = sin x и y = 1 . На отрезке 2
[− π ; 2π ] эти графики (рисунок 7.3) пересекаются в двух точках с абсциссами
π , 5π . Это и есть корни исходного уравнения.
66
π |
|
5π |
||
Ответ. x |
|
, |
|
. |
|
|
|||
|
6 |
|
6 |
|
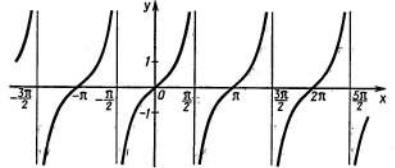
Рисунок 7.3. Графики функции y = sin x и y = |
1 |
|
|||||||||
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|||
Задача 2. Найти |
все решения неравенства |
sin x < |
1 |
, принадлежащие |
|||||||
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
||
отрезку −π ≤ x ≤ 2π . |
|
|
|
|
|
|
|
|
|
|
|
Решение. Из рисунка 7.3 видно, что график функции y = sin x лежит ниже |
|||||||||||
|
1 |
|
|
π |
|
5π |
|
|
|||
графика функции y = |
|
|
на промежутках −π; |
и |
|
; 2π . |
|||||
|
|
|
|||||||||
|
2 |
|
|
6 |
|
6 |
|
|
|||
|
|
|
|
76 |
|
π |
|
5π |
|
Ответ. x −π; |
|
|
|
; 2π . |
|
||||
|
6 |
|
6 |
|
Упражнения
1. Сравнить числа, используя свойство возрастания и убывания функции
y = sin x
1.1. sin |
7π |
и sin |
13π |
; |
|
|
1.2. sin |
13π |
и sin |
11π |
; |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
10 |
|
|
|
|
10 |
|
|
|
|
|
|
|
7 |
|
|
|
7 |
|
|
|
|
||
|
|
7π |
|
|
8π |
|
|
|
8π |
|
|
|
|
9π |
||||||||||
1.3. |
sin − |
|
|
и |
sin |
− |
|
; |
1.4. |
sin |
− |
|
|
и |
sin |
− |
|
; |
||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
8 |
|
|
9 |
|
|
|
7 |
|
|
|
|
8 |
|||||||||
1.5. sin3и sin 4; |
|
|
|
|
|
1.6. sin 7 и sin 6 . |
|
|
|
|
||||||||||||||
2. Найти корни уравнения, принадлежащие отрезку [0; 3π ]
2.1. sin x = |
|
|
3 |
|
; |
|
1.2. sin x = |
|
|
|
2 |
|
; |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2.3. sin x = − |
|
2 |
; |
1.4. sin x = − |
3 |
|
. |
|||||||||||||
2 |
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3. Найти решения неравенств, принадлежащие отрезку [0; 3π ] |
||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3.1. sin x > |
; |
|
3.2. sin x ≤ |
|
|
2 |
; |
|
|
|||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|||||||||||||
3.3. sin x ≥ − |
; |
3.4. sin x < − |
|
3 |
. |
|||||||||||||||
|
||||||||||||||||||||
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||
4. Сравнить числа, выражая косинус через синус по формулам приведения 2.7
4.1. sin π и cosπ ; |
4.2. sin |
9π |
и cos |
9π |
; |
||||
|
|
|
|||||||
9 |
9 |
|
8 |
8 |
|
||||
4.3. sin π и cos |
5π |
; |
4.4. sin π и cos |
3π |
. |
||||
|
|
||||||||
5 |
14 |
|
8 |
10 |
|
|
|||

77
5. Найти корни уравнения, принадлежащие промежутку − 3π ≤ x ≤ π 2
5.1. sin 2x = − |
1 |
; |
5.2. sin3x = |
3 |
. |
|
|
||||
2 |
|
2 |
|
||
6. Найти решения неравенства, принадлежащие промежутку − 3π ≤ x ≤ π 2
6.1. sin 2x ≥ − |
1 |
; |
6.2. sin3x < |
3 |
. |
|
|
||||
2 |
|
2 |
|
||
7. Построить график функции и выяснить её свойства
7.1. |
y = 1− sin x ; |
7.2. |
y = 2 + sin x ; |
7.3. |
y = sin 3x ; |
7.4. |
y = 2sin x . |
8. Найти множество значений функции y = sin x , если x принадлежит промежутку
|
π |
|
|
|
|
3π |
|
5π |
|
8.1. |
|
; π |
; |
8.2. |
|
|
; |
|
. |
|
|
||||||||
|
6 |
|
|
|
|
4 |
|
4 |
|
|
|
9. Построить график функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
9.1. y = sin |
|
x |
|
; |
|
|
|
|
|
|
|
9.2. |
y = |
|
|
sin x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
Ответы. |
1.1. |
|
sin |
7π |
|
> sin |
13π |
; |
|
1.2. |
|
|
sin |
13π |
> sin |
11π |
; |
|
1.3. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
7 |
|
|
|
|
|
|
|
||||||||||||
|
|
7π |
|
|
8π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8π |
|
|
|
|
|
|
|
|
9π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
sin |
− |
|
|
> sin − |
|
|
|
; |
1.4. |
|
|
sin |
− |
|
|
|
|
|
|
|
> sin |
− |
|
|
; |
1.5. |
|
sin3 > sin 4; |
1.6. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
8 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
sin7 > sin6. 2.1. x = π ; |
2π |
; |
7π |
; |
8π |
; 2.2. x = π ; |
3π |
; |
9π |
; |
11π |
; |
2.3. x = |
5π |
; |
7π |
; |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
4 |
4 |
|
|
|
4 |
|
4 |
|
|
|||||||||||||||||||||
2.4. |
x = |
4π |
; |
5π |
. |
3.1. |
π < x < |
5π |
; |
13π |
< x < |
17π |
; |
3.2. |
0 ≤ x < π ; |
3π |
≤ x < |
9π |
; |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
6 |
|
|
|
|
6 |
|
|
|
|
6 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
4 |
|
4 |
|
|
|
|
4 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
78 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3. |
|
0 ≤ x < |
7π |
; |
11π |
≤ x < 3π; |
3.4. |
|
4π |
< x < |
5π |
. |
|
|
|
4.1. |
sin π < sin |
7π |
; 4.2. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
6 |
|
6 |
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
9 |
|
18 |
|
|
|||||||||||||||
sin |
9π |
> cos |
9π |
; 4.3.sin π > sin π ; 4.4.sin π < cos |
3π |
. 5.1. x = − |
17π |
; − |
13π |
; |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
8 |
|
|
|
8 |
|
|
5 |
7 |
|
|
8 |
10 |
|
|
|
|
|
12 |
12 |
|
|
||||||||||||||||||||||||
− |
5π |
; − |
π |
; |
5π |
; |
11π |
; 5.2. x = − |
11π |
; − |
10π |
; − |
5π |
; − |
4π |
; π ; |
2π |
; |
7π |
; |
8π |
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
12 |
|
12 |
12 |
|
|
12 |
|
|
9 |
|
|
9 |
|
|
9 |
|
|
|
|
|
9 |
9 |
9 |
|
9 |
|
9 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.5. Функция y = tgx , её свойства и график |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
Основные свойства функции y = tgx |
(рисунок 7.4) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1.Область определения – множество R всех действительных чисел кроме x = π + πn, n Z.
2
2.Множество значений – множество R всех действительных чисел.
3.Функция y = tgx периодическая с периодом π .
4.Функция y = tgx нечётная.
5.Функция y = tgx принимает
- значение, равное 0, при x = πn , n Z; |
|
|
|
|
πn; |
π |
|
- положительные значения на интервалах |
|
+πn , n Z; |
|
|
|
2 |
|
|
− |
π |
|
- отрицательные значения на интервалах |
|
+πn;πn , n Z. |
|
|
|
2 |
|
6. Функция y = tgx |
|
− |
π |
+πn; |
π |
|
возрастает на интервалах |
|
|
+πn , n Z. |
|||
|
|
|
2 |
|
2 |
|
Рисунок 7.4. График функции y = tgx

79
Задача 1. Найти все корни уравнения tgx = 2, принадлежащее отрезку
−π ≤ x ≤ 3π . 2
Решение. Рассмотрим графики функций y = tgx и y = 2 (рисунок 7.4). На
|
|
3π |
|
|
отрезке |
−π; |
|
|
эти графики пересекаются в трёх точках с абсциссами |
|
||||
|
|
2 |
|
|
arctg2;arctg2 + π ; arctg2 − π . Это и есть корни исходного уравнения.
Ответ. x {arctg2;arctg2 + π; arctg2 − π}.
Задача 2. Найти все решения неравенства tgx ≤ 2 , принадлежащие
отрезку −π ≤ x ≤ 3π . 2
|
Решение. Из рисунка 7.4. видно, что график функции y = tgx |
лежит не |
|||||||||||
|
|
|
|
|
|
|
|
− |
π |
;arctg2 |
|
, |
|
выше графика функции y = 2 на промежутках [−π;−π + arctgx ], |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; π +arctg2 . |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
π |
|
|
π |
; π +arctg2 |
|
|
|
|
|
|
|
Ответ.x [−π;−π + arctgx ] |
|
;arctg2 |
|
|
. |
|
|
|
||||
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
Задача 3. Решить неравенство tgx > 1.
Решение. Из рисунка 7.4. видно, что график функции y = tgx лежит
выше графика прямой |
y = 1 |
π |
; |
π |
|
|||
на промежутке |
|
, а также на промежутках, |
||||||
|
|
|
|
|
4 |
|
2 |
|
полученных сдвигами его на π , 2π , 3π , − π , − 2π... . |
|
|||||||
|
π |
+ |
πn; |
π |
|
|
|
|
Ответ. x |
|
|
+πn , n Z. |
|
|
|
||
|
4 |
|
|
2 |
|
|
|
|
